Lexikon der Chemie: NMR-Spektroskopie
NMR-Spektroskopie (Abk. von engl. nuclear magnetic resonance), Kernresonanzspektroskopie, Kernspinresonanzspektroskopie, kernmagnetische Resonanzspektroskopie, Abk. KMR, magnetische Kernresonanzspektroskopie, Abk. MKR, Kerninduktion, Teilgebiet der Spektroskopie, das auf radiofrequenz-induzierten Übergängen zwischen Energieniveaus beruht, die Atomkerne in einem äußeren Magnetfeld infolge ihres eigenen magnetischen Momentes einnehmen.
Die NMR-S. hat sich infolge ihrer großen Leistungsfähigkeit zu einer auf zahlreichen Gebieten der festkörperphysikalischen, chemischen und physikochemischen Forschung sehr erfolgreich eingesetzten analytischen Methode entwickelt, die hinsichtlich struktureller Informationen insbesondere organischer Verbindungen von kaum einer anderen Methode übertroffen werden kann.
Theoretische Grundlagen. Neben Kernladung und Masse haben zahlreiche Atomkerne einen Eigendrehimpuls (Spin) p, der sich durch vektorielle Addition aus den Drehimpulsen der Nucleonen (Protonen und Neutronen) zusammensetzt. Ebenso wie andere atomare Größen ist dieser Eigendrehimpuls p gequantelt und beträgt
(1)
Dabei ist I die Kernspinquantenzahl, die für die verschiedenen Atomkerne ganz- oder halbzahlige Werte zwischen 0 und 6 annehmen kann, h ist das Plancksche Wirkungsquantum. Da jede rotierende elektrische Ladung einem magnetischen Moment entspricht, ist mit dem Eigendrehimpuls p der Kerne ein magnetisches Moment μ verknüpft: μ = γ·p (2). Die Proportionalitätskonstante γ wird als gyromagnetisches oder magnetogyrisches Verhältnis bezeichnet und ist für jede Atomart eine charakteristische Größe. Aus den Kerneigenschaften einiger wichtiger Atomkerne (Tab. 1) ist ersichtlich, daß alle Kerne mit gerader Protonen- und gerader Neutronenzahl (g,g-Kerne) die Kernspinquantenzahl 0 aufweisen und demzufolge kein magnetisches Moment haben. Zu dieser Gruppe gehören solche wichtigen Kerne wie 12C, 16O, 32S. Sie umfaßt etwa 60 % aller stabilen Atomkerne, die mit Hilfe der NMR-S. nicht untersucht werden können. Nur diejenigen Atomkerne haben magnetische Momente, bei denen entweder die Protonen- oder die Neutronenzahl oder beide ungeradzahlig sind, wobei ganzzahlige Kernspinquantenzahlen bei den u,u-Kernen (ungeradzahlige Protonen- und ungeradzahlige Neutronenzahl, z. B. 14N), halbzahlige bei den g,u- und u,g-Kernen (z. B. 13C und 11B) vorkommen. Bringt man Atomkerne mit einem magnetischen Moment, die man sich als kleine Elementarmagnete vorstellen kann, in ein äußeres magnetisches Feld der Feldstärke H0 so werden sie dort zur äußeren Feldrichtung ausgerichtet. Infolge der in atomaren Dimensionen geltenden Quantenbedingungen ist nur eine begrenzte Anzahl von Orientierungen bzw. Spinzuständen – nämlich 2I+ 1 – möglich, für die die Projektion des Drehimpulsmomentes auf die Feldrichtung (z-Achse des Koordinatensystems) pz halb- oder ganzzahlige Vielfache des Elementarimpulses h/2π sein muß. Die 2I + 1 möglichen Projektionen werden durch die magnetische Quantenzahl m charakterisiert, die alle Werte von + I, I – 1, ... - I annehmen kann: pz = m(h/2π) (3) (Abb. 1).

NMR-Spektroskopie. Abb. 1: Erlaubte Orientierungen der magnetischen Momente von Kernen mit I = 1/2 (a) und I = 1 (b).
Für die Komponente des magnetischen Momentes μ in der Feldrichtung z ergibt sich daraus
μz = γpz = γm(h/2π). (4)
Für Kerne mit I = 1/2, die am häufigsten untersucht werden, ergibt sich eine parallele (m= +1/2) und eine antiparallele (m= -1/2) Einstellung, die sich in ihrem Energiegehalt unterscheiden und sich in einem Termschema darstellen lassen. Die Energie E eines magne.tischen Dipols in einem äußeren Magnetfeld H0 beträgt
. (5)
Somit entsprechen die aufgezeigten Kernorientierungen potentiellen Energien von E+= +1/2γH0(h/2π) und E-= -1/2γH0(h/2π) (Abb. 2). Im Unterschied zu anderen Spektroskopiearten sind diese Energieniveaus nicht in der Substanz vorhanden, sondern sie werden erst durch das äußere Magnetfeld erzeugt. Die Verteilung der Kerne auf diese Energieniveaus wird im thermischen Gleichgewicht durch die Boltzmann-Verteilung bestimmt. Es läßt sich damit zeigen, daß bei Zimmertemperatur und einem Magnetfeld von 1,4 T (Tesla) im Falle des 1H-Kerns auf 1000000 Kerne in der energiereicheren antiparallelen Anordnung 1000003 Kerne in der energieärmeren parallelen Orientierung kommen, d. h., daß die Besetzungsunterschiede äußerst gering sind. Zwischen den in Abb. 2 eingezeichneten Energiezuständen können mit Hilfe elektromagnetischer Strahlung geeigneter Energie Übergänge induziert werden. Sie bestehen in einer Umorientierung der Richtung des magnetischen Kernmomentes im äußeren Magnetfeld. Da die Energiedifferenz zwischen beiden Zuständen ΔE = γH0(h/2π) (6) beträgt, ergibt sich unter Verwendung der Frequenz/Energie-Beziehung ΔE = h·ν die Resonanzbedingung ν = γH0/2π. (7)
Sie gibt an, welche Frequenz elektromagnetischer Strahlung mit einem bestimmten Atomkern (charakterisiert durch dessen gyromagnetisches Verhältnis) bei einer äußeren Feldstärke H0 in Resonanz (Energieaustausch) tritt. Für Übergänge zwischen den Spinniveaus gilt die Auswahlregel Δm = ±1. Aus Gl. (6) folgt, daß die Spinzustände außerhalb des Magnetfeldes (H0 = 0) gleiche Energie haben, während ihre Energie bzw. Energiedifferenz um so größer ist, je stärker das Magnetfeld ist, in dem sich die Kerne befinden (Abb. 3). Die gewöhnlich in der NMR-S. verwendeten Feldstärken von 1,4 bis 9,4 T entsprechen beim 1H-Kern Resonanzfrequenzen von 60 bis 400 MHz, was etwa der Strahlung aus dem Radiowellenbereich entspricht.
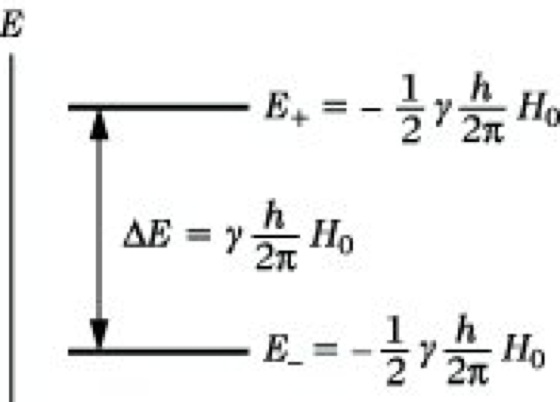
NMR-Spektroskopie. Abb. 2: Energieniveasus eines Kerns mit I = 1/2 in einem äußeren Magnetfeld.
Wie aus Tab. 1 ersichtlich, weisen die Atomkerne 1H, 11B, 19F, 31P sowohl eine hohe natürliche Häufigkeit als auch ein großes gyromagnetisches Verhältnis auf. Aus Gründen der Empfindlichkeit werden vor allem diese Elemente, jedoch auch 13C-Kerne (s. u.) mit Hilfe der NMR-S. untersucht. Am bedeutendsten ist die Untersuchung von 1H-Kernen, so daß im folgenden vor allem auf die Untersuchung dieser Kerne (1H-NMR-Spektroskopie oder PMR-Spektroskopie [Abk. von engl. proton magnetic resonance] eingegangen werden soll.

NMR-Spektroskopie. Abb. 3: Energie der Kernorientierungen in Abhängigkeit von der magnetischen Feldstärke.
NMR-Spektroskopie. Tab. 1: Eigenschaften einiger Atomkerne.
| |||||
| 1H | 99 | ,98 | 1/2 | 2,6738 | 1,00 |
| 2D | 0 | ,016 | 1 | 0,4104 | 0,01 |
| 11B | 80 | ,42 | 3/2 | 0,8583 | 0,165 |
| 12C | 98 | ,9 | 0 | 0 | |
| 13C | 1 | ,1 | 1/2 | 0,6724 | 0,016 |
| 14N | 99 | ,63 | 1 | 0,1926 | 0,001 |
| 16O | 99 | ,76 | 0 | 0 | |
| 19F | 100 | 1/2 | 2,5161 | 0,834 | |
| 31P | 100 | 1/2 | 1,0828 | 0,066 | |
| 35Cl | 75 | ,4 | 3/2 | 0,2628 | 0,005 |
| 55Mn | 100 | 5/2 | 0,6625 | 0,175 | |
| 209Bi | 100 | 9/2 | 0,4298 | 0,137 |
*) bei gleicher Kernzahl und H0 = konst. bezogen auf 1H = 1,00 (H0 ist die äußere magnetische Feldstärke).
Aus dem geringen Besetzungsunterschied zwischen den Energieniveaus resultiert eine geringe Intensität der beobachteten Signale. Durch die Messung wird dies noch ungünstiger gestaltet, da eine allmähliche Auffüllung des oberen Niveaus erfolgt. Ist dies geschehen, so kann keine nach außen feststellbare Absorption mehr erfolgen. Es ist "Sättigung" eingetreten. Durch diesen Vorgang wäre an und für sich jede Möglichkeit NMR-spektroskopischer Untersuchungen zeitlich begrenzt, wenn nicht durch Relaxationsvorgänge die überschüssige Energie strahlungslos an die Umgebung (z. B. auf benachbarte Atome oder Moleküle – allgemein Gitter genannt) übertragen werden könnte. Man spricht deshalb von Spin-Gitter-Relaxation. Der zeitliche Verlauf dieser Prozesse wird durch die Spin-Gitter-Relaxationszeit T1 beschrieben, d. i. die Zeit, die erforderlich ist, um 1/e der Überschußenergie abzugeben. T1 schwankt je nach der untersuchten Probe stark (100 bis 10-4 S), wobei im allg. in Flüssigkeiten und Gasen kurze T1-Werte beobachtet werden. Von der Spin-Gitter-Relaxationszeit hängt z. B. ab, wie hoch man die Intensität der Radiofrequenz-(RF)-Strahlung wählen kann, ohne daß der erwähnte Sättigungsprozeß eintritt. Die im NMR-Spektrometer gemessenen Signale hängen in ihrer Form vom Aggregatzustand der untersuchten Probe ab. An flüssigen Proben erhält man scharfe Signale (hochauflösende NMR-S.). Diese Methode hat für den Chemiker die größte Bedeutung. Kristalline Verbindungen ergeben breite Signale (Breitband-NMR-S.).
1) Hochauflösende NMR-S. Hier werden die Proben im flüssigen Zustand, meist in einem Lösungsmittel, untersucht. Dieses sollte die zu untersuchende Kernsorte nicht selbst enthalten. 1H-NMR-Untersuchungen werden deshalb vorwiegend in wasserstofffreien bzw. deuterierten Lösungsmitteln, z. B. Kohlenstofftetrachlorid, Kohlendisulfid, Chloroform-d1, Methanol-d4, Aceton-d5, Dimethylsulfoxid-d6, durchgeführt. Die Proberöhrchen haben einen Durchmesser von 5 mm und sollten im Falle der 1H-NMR-S. etwa 1017 Protonen enthalten.
Die Hauptbauelemente eines NMR-Spektrometers (Abb. 4) sind: 1) ein Magnet mit hoher und konstanter Feldhomogenität über das Probevolumen, 2) ein RF-Sender von einer Stabilität, die der hohen Feldhomogenität äquivalent ist, und 3) ein hochempfindlicher RF-Empfänger.

NMR-Spektroskopie. Abb. 4: Blockschema eines NMR-Spektrometers mit CW-Technik (Abk. von continous wave).
Die Probe befindet sich im Proberöhrchen zwischen den Polschuhen des Magneten. Nachdem sich das der Boltzmann-Verteilung entsprechende Gleichgewicht eingestellt hat, wirkt das vom RF-Sender erzeugte elektromagnetische Wechselfeld über eine Spule auf die Probe ein. Befinden sich die Frequenz und das angelegte Magnetfeld H0 in Übereinstimmung mit der Resonanzbedingung Gl. (7), so kommt es zu einer Energieabsorption, die mit Hilfe des RF-Empfängers gemessen und über eine entsprechende Verstärkereinrichtung auf einem Schreiber registriert wird. Man erhält eine graphische Darstellung, ein NMR-Spektrogramm, in dem die Energieabsorption gegen die eingestrahlte Frequenz aufgetragen ist (Abb. 6).
Die Resonanzbedingung kann erreicht werden 1) durch Variation der Frequenz des eingestrahlten elektromagnetischen Wechselfeldes bei konstantem Magnetfeld (Frequenz-Sweep) und 2) durch Variation des Magnetfeldes bei konstanter Frequenz (Feld-Sweep). Beide Verfahren faßt man unter dem Begriff continous-wave-(CW-)Verfahren zusammen, um auszudrücken, daß bei beiden Verfahren eine physikalische Größe kontinuierlich verändert wird. Davon zu unterscheiden ist die Puls-Fourier-Transform-Technik (s. u.).
Das experimentelle Hauptproblem bei NMR-Geräten sind die außerordentlich hohen Anforderungen an die Konstanz und Homogenität des Magnetfeldes bzw. der Radiofrequenzen, die in der Größenordnung von 10-8 und besser sein müssen.
Einen Überblick über die einem NMR-S. entnehmbaren Spektrenparameter und die daraus erhältlichen Aussagen gibt Tab. 2.
NMR-Spektroskopie. Tab. 2: Informationsgehalt von Spektrenparametern in der hochauflösenden NMR-Spektroskopie.
| |||||
| Anzahl unterschiedlicher Atomgruppen | Art der Gruppen | Anzahl der Atome je Gruppe | Anzahl der benach- barten Kerne | Art und Abstand der Nachbarkerne |
Chemische Verschiebung δ. Das gyromagnetische Verhältnis stellt für jedes Isotop eine charakteristische Größe dar, so daß für verschiedene Kernsorten bei konstanter äußerer Feldstärke unterschiedliche Resonanzfrequenzen erhalten werden, die sich oft um einige MHz unterscheiden (Abb. 5). Viel wichtiger für die chemische Anwendung der NMR-S. ist jedoch die Tatsache, daß für Atome der gleichen Art je nach ihrer chemischen Umgebung geringfügig unterschiedliche Resonanzfrequenzen gefunden werden. So beobachtet man im 1H-NMR-Spektrogramm des Benzylalkohols (Abb. 6) 3 Signale, die den 3 unterschiedlich gebundenen Wasserstoffkernen entsprechen. Ursache dafür ist, daß am Ort des jeweiligen Atomkerns nicht das von außen angelegte Feld H0 wirksam ist, sondern ein effektives Feld Heff, das infolge der Abschirmung der Kerne durch ihre Elektronenhülle einen von H0 leicht unterschiedlichen Wert der Größe Heff = H0(1 – σ) annimmt. Das Zusatzfeld H0σ ist um so stärker, je stärker H0 ist. Hierbei ist σ die Kernabschirmungskonstante, die sehr klein ist und für Protonen in der Größenordnung von 10-5 liegt. Für ein Magnetfeld von 2,3 T liegen die Resonanzfrequenzen etwa zwischen 100000000 Hz und 100001500 Hz. Um diese großen Zahlenwerte bei der Angabe von Signallagen zu vermeiden, arbeitet man bei ihrer Angabe nicht mit den absoluten Frequenzen, sondern mißt sie relativ zur Absorption einer Standardsubstanz, die den Nullpunkt der Frequenzskale bildet. Als eine solche Standardsubstanz wird neuerdings nahezu ausschließlich Tetramethylsilan (TMS) verwendet, das meist der zu untersuchenden Lösung als innerer Standard in geringen Mengen zugesetzt wird. Da verschiedene Spektrometermodelle mit unterschiedlichen Feldstärken arbeiten und die Resonanzfrequenzen von H0 abhängig sind, muß zur zahlenmäßigen Angabe der Signallage eine Skale mit feldunabhängigen Einheiten gewählt werden. Diese als chemische Verschiebung bezeichnete Einheit δ erhält man, indem man die Frequenzdifferenz zwischen dem Signal der Probe νσ und der Standardsubstanz νs durch die Freqzenz der Standardsubstanz im betreffenden Magnetfeld (Arbeitsfrequenz) ν0 dividiert
(8)
NMR-Spektroskopie. Abb. 5: Absorptionsfrequenzen einiger Atomkerne bei 2,35 T magnetischer Feldstärke.

NMR-Spektroskopie. Abb. 6: 1H-NMR-Spektrogramm von Benzylalkohol C6H5-CH2-OH (Arbeitsfrequenz 60 Mhz).
Da νσ – νs in Hz, ν0 in MHz ausgedruckt werden, erhält man für den dimensionslosen Parameter δ die Einheit 10-6 oder ppm (engl. parts per million). Die chemische Verschiebung von TMS ist also definitionsgemäß 0, die chemischen Verschiebungen der meisten Wasserstoffkerne in organischen Verbindungen sind größer als 0, d. h., ihre Signale erscheinen in der üblichen Darstellung der NMR-S. links vom TMS-Signal. Mitunter werden chemische Verschiebungen in τ-Werten ausgedrückt, die mit den δ-Werten durch die folgende Beziehung verbunden sind:
τ = 10 – δ. (9)
Empirisch ermittelte Bereiche der chemischen Verschiebung können zum Nachweis bestimmter Protonengruppierungen verwendet werden und sind somit zur Strukturaufklärung unbekannter Verbindungen von großer Bedeutung (Abb. 7). Zur Kennzeichnung der Lage eines Resonanzsignals gegenüber einem anderen sind eine Reihe unterschiedlicher Bezeichnungen im Gebrauch (Abb. 8).
Signalintensität. Als Signalintensität wird in der NMR-S. die Fläche unter dem Resonanzsignal bezeichnet. Da die Signalintensitäten von den apparativen Bedingungen des Spektrometers abhängig sind, ermittelt man nicht ihre absoluten Werte, sondern die Intensitätsverhältnisse der einzelnen Signale.

NMR-Spektroskopie. Abb. 7: Erwartungsbereiche der chemischen Verschiebung für unterschiedlich gebundene Protonen.
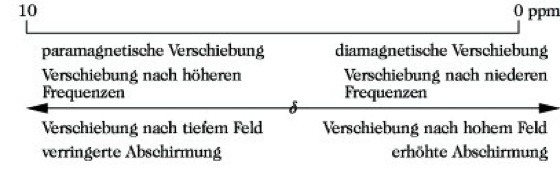
NMR-Spektroskopie. Abb. 8: Bezeichnungen für die Verschiebung eines Kernresonanzsignals.
Von modernen NMR-Spektrometern können die Signalflächen integriert und die Integralstufen ins Spektrum eingezeichnet werden. Das Intensitätsverhältnis der Signale ist dann identisch mit dem Verhältnis der Stufenhöhen der Integralkurve. In der 1H-NMR-S. ist die Intensität eines Signals normalerweise direkt proportional der Anzahl der 1H-Kerne, die dieses Signal hervorrufen. Besteht die Probe aus einer einheitlichen Verbindung, dann lassen sich aus den Intensitätsverhältnissen unmittelbar die Mengenverhältnisse unterschiedlich gebundener Kerne angeben (Abb. 9).

NMR-Spektroskopie. Abb. 9: 1H-NMR-Spektrum von Ethylbromid CH3-CH2Br, Arbeitsfrequenz 60 Mhz.
Multiplizität.In der NMR-S. werden häufig Signalaufspaltungen (Multipletts) beobachtet, die nicht auf unterschiedliche chemische Verschiebungen zurückgeführt werden können. Sie haben ihre Ursache in den magnetischen Momenten benachbarter Kerne. Das 1H-NMR-Spektrum von 1,1,2-Trichlormethan ist schematisch in Abb. 10 dargestellt. Der magnetische Kern HA baut um sich ein Magnetfeld auf. Dieses Feld wird durch die Bindungselektronen zu den Kernen HX übertragen. An diesen Kernen erscheint ein kleines Zusatzfeld, das das Resonanzsignal geringfügig verschiebt. Da der Kern HA entweder parallel oder antiparallel zum äußeren Magnetfeld eingestellt ist, ergibt sich an den HX-Kernen ein positives oder negatives Zusatzfeld gleicher Größe. Ein aus vielen Kernen HX resultierendes Signal erscheint demzufolge als Dublett. Die beiden äquivalenten Kerne HX rufen am Kernort HA drei Zusatzfelder hervor, je nachdem, ob sich a) die beiden Spins addieren und parallel zum äußeren Magnetfeld stehen, b) sich gegenseitig kompensieren oder c) sich addieren und antiparallel zum äußeren Feld stehen. Das Signal von HA erscheint folglich als Triplett. Die Multiplizität M eines Signals ergibt sich allgemein zu M= 2nI + 1, wobei n die Anzahl der benachbarten magnetischen Kerne, I ihre Kernspinquantenzahl bedeuten. Für Kerne, wie 1H, 13C, 19F, 31P, mit I = 1/2 vereinfacht sich diese Beziehung zu M = n + 1. Kopplungen zwischen äquivalenten Kernen (z. B. den beiden HX-Kernen) werden nicht beobachtet. Die Linienintensitäten innerhalb eines Multipletts folgen den Binomialkoeffizienten, d. h., sie verhalten sich in einem Dublett wie 1 : 1, in einem Triplett wie 1 : 2 : 1 und in einem Quartett wie 1 : 3 : 3 : 1. Als weiteres Beispiel für die Multiplizität sei auf das 1H-NMR-Spektrum des Ethylbromids (Abb. 9) verwiesen, in dem die 1H-Kerne der CH3-Gruppe als Triplett, die der CH2-Gruppe als Quartett erscheinen. Der Abstand benachbarter Einzellinien in einem Multiplett wird durch die Kernspinkopplungskonstante, kurz Kopplungskonstante, J angegeben. Da die Frequenzdifferenzen zwischen den Linien eines Multipletts nur durch die unterschiedlichen Orientierungen der Nachbarspins zustande kommen, sind sie von der Arbeitsfrequenz des Gerätes unabhängig und werden in Hz gemessen. Ihre Größe wird durch Faktoren wie Art und Abstand der koppelnden Kerne, Art der Bindung zwischen diesen Kernen sowie durch die geometrische Anordnung der koppelnden Kerne zueinander (Konfiguration, Konformation) bestimmt. Ebenso wie für die chemischen Verschiebungen gibt es auch für die Kopplungskonstanten empirisch aufgestellte Tabellen, die ihre Größe in Abhängigkeit von bestimmten Strukturen angeben und somit für die Strukturaufklärung wesentlich sind. Je nach dem Abstand der koppelnden Kerne unterscheidet man geminale Kopplungen (über 2 Bindungen wie im Strukturelement H-C-H), vicinale Kopplungen (über 3 Bindungen wie in
H-C-C-H) und weitreichende (longe range) Kopplungen über mehr als 3 Bindungen. Der Betrag von J nimmt mit zunehmender Entfernung der koppelnden Kerne ab.
Spektren höherer Ordnung. In den bisher betrachteten NMR-Spektren konnten die chemischen Verschiebungen und Kopplungskonstanten direkt aus dem Spektrum entnommen werden. Das ist immer dann der Fall, wenn die Frequenzdifferenz zwischen den Signalen Δν groß gegenüber ihren Kopplungskonstanten J sind (Spektren 1. Ordnung). Ist dagegen Δν kleiner als die sechsfache Kopplungskonstante Δν/J ≤ 6, so liegen Spektren höherer Ordnung vor, für deren Deutung die einfachen Regeln über die Multiplizität sowie die Linienabstände und -intensitäten in Multipletts versagen. Eine exakte Spektrenanalyse ist nur mit aufwendigen Rechenmethoden möglich. Spektren höherer Ordnung treten häufig in der praktischen NMR-S. auf und erschweren die Auswertung der Spektren erheblich.
Bezeichnung von Spinsystemen. Um die Beziehung zwischen den verschiedenen Kernen oder Gruppen von äquivalenten Kernen eines Spinsystems anzuzeigen, werden alle miteinander koppelnden Kerne mit Großbuchstaben benannt. Äquivalente Kerne erhalten den gleichen Buchstaben. Ihre Anzahl wird als Index angehängt. Sind die chemischen Verschiebungen der koppelnden Kerne sehr verschieden, dann bezeichnet man sie mit Buchstaben vom Beginn und vom Ende des Alphabets. Gibt es weitere Kerne, die in ihren chemischen Verschiebungen dazwischen liegen, erhalten sie die Buchstaben M, N, O. Sind die chemischen Verschiebungen der Kerne ähnlich, wie das bei Spektren höherer Ordnung der Fall ist, werden sie mit aufeinanderfolgenden Buchstaben bezeichnet.
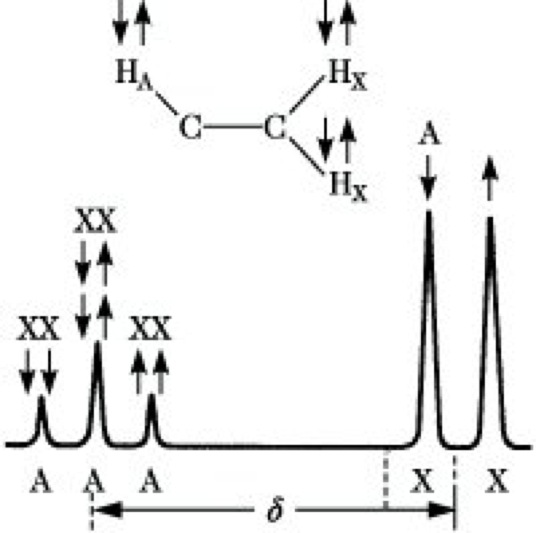
NMR-Spektroskopie. Abb. 10: Spin-Spin-Kopplung in 1,1,2-Trichlorethan.
Beispiele: Im 1,1,2-Trichlormethan (Abb. 10) liegt ein AX2- oder A2X-Spektrum, im Ethylbromid (Abb. 9) ein A3X2-Spektrum, im 1-Chlorpropen CH3-CH=CHCl ein A3XY-System, im Ethanol CH3-CH2-OH ein A3M2X-System vor. Im Dichloracetaldchyd CCl2H-CHO spricht man von einem AX-System, in einem disubstituierten Alken RHC= CHR', in dem sich die beiden Protonen in ihrer chemischen Verschiebung nur wenig unterscheiden, von einem AB-System. Das AB-System gehört zu den Spektren höherer Ordnung.
Vereinfachung komplizierter Spektren.Es sind eine Reihe von Methoden entwickelt worden. 1) Erhöhung der magnetischen Feldstärke. Die Differenzen der chemischen Verschiebung zweier Signale nehmen mit zunehmender Feldstärke zu, dagegen sind die Kopplungskonstanten von der Feldstärke unabhängig, so daß die Bedingung für das Auftreten von Spektren 1. Ordnung um so eher erfüllt ist, je höher die Feldstärke des Spektrometers ist. Wenn eine Probe bei 60 MHz ein komplexes Spektrum ergibt, so wird dieses bei 100 MHz oder 220 MHz normalerweise deutlich vereinfacht, wobei der Grad der Verbesserung allerdings von den speziellen Spektrenparametern abhängig ist.
2) Spinentkopplung (auch Doppelresonanz genannt, da gleichzeitig zwei Frequenzen eingestrahlt werden). Wenn zwei Kerne vom Spin 1/2 in einem AX-System miteinander koppeln, so beobachtet man 4 Signale im Spektrum (Abb. 11). Wird jedoch der Kern HX während der Registrierung zusätzlich intensiv mit seiner Resonanzfrequenz νX bestrahlt, so beobachtet man anstelle des ursprünglichen Dubletts für HA nur noch ein Singulett. Das Signal von HA ist spinentkoppelt. Man kann sich dies durch folgende vereinfachte Vorstellung erklären. Die Einstrahlung der Frequenz verursacht ein sehr schnelles Umklappen der HX-Kerne, so daß am Kernort der HA-Kerne keine zwei Zusatzfelder entsprechend der parallelen und antiparallelen Einstellung der HX-Kerne im äußeren Magnetfeld wirksam werden, sondern ein aus beiden Einstellungen gemitteltes Zusatzfeld. Erfolgt eine Entkopplung von gleichen Kernen, z. B. von zwei H-Kernen HA und HX, so spricht man von homonuclearer Entkopplung, werden Kerne verschiedener Elemente (z. B. 1H und 19F oder 1H und 13C) entkoppelt, so liegt eine heteronucleare Entkopplung vor. Enthält das zusätzliche Hochfrequenzfeld alle Resonanzfrequenzen der 1H-Kerne (Breitband- oder Rauschentkopplung), so können damit z. B. alle 1H-13C-Kopplungen beseitigt werden, was für die Vereinfachung von 13C-NMR-Spektren wesentlich ist. Neben der Vereinfachung des Spektrums gibt die Spinentkopplung Aufschluß über die Zusammengehörigkeit bestimmter Signale.

NMR-Spektroskopie. Abb. 11: Spinentkopplung in einem AX-System
3) Verschiebungsreagenzien (shift reagents). Mit der Verwendung paramagnetischer Komplexe (Paramagnetismus) der Seltenerdmetalle als Verschiebungsreagenzien wurde ein Weg zur Spreizung überlappender Signale gefunden. Häufig verwendete Verschiebungsreagenzien sind: Eu(dpm) 3, Eu(fod)3, Pr(dpm)3 und Pr(fod)3, wobei mit dpm der Dipivaloyl-methanato-Rest, mit fod der 1,1,1,2,2,3,3-Heptafluoro-7,7-dimethyl-4,6-octan-dionato-Rest (Abb. 12) abgekürzt wird. Durch Wechselwirkung mit freien Elektronenpaaren aus polaren Gruppen der Probe, z. B. --OH, -NH2, /C=O, -O-, -COOR, kann sich die Koordinationszahl des Metalls erhöhen, und die Probe kann über ihre polaren Gruppen reversibel mit dem Lanthanoidenkomplex koordinieren. In dem gebildeten Komplex wirken die lokalen Magnetfelder des paramagnetischen Metall-Ions auf die verschiedenen Kerne der Probe ein und verschieben aufgrund ihres Magnetfeldes die Signale im NMR-Spektrum um so mehr, je geringer der Abstand zwischen dem paramagnetischen Metall-Ion und dem untersuchten Kern ist. So beobachtet man im normalen 1H-NMR-Spektrum von Hexanol HO-CH2-CH2-CH2-CH2-CH2-CH3 für die mittleren CH2-Gruppen ein nicht aufgelöstes breites Signal. Nach Zugabe von Eu(dpm)3 erscheinen für jede CH2-Gruppe deutlich getrennte Signale, wobei die Größe der Verschiebung aus der ursprünglichen Lage vom Abstand der betreffenden CH2-Gruppe vom Koordinationszentrum (OH-Gruppe) abhängig ist.

NMR-Spektroskopie. Abb. 12: Verschiebungsreagenz. M = Seltenerdmetall.
13C-NMR-Spektroskopie. Durch Untersuchung an 13C-Kernen mittels der NMR-S. kann das Kohlenstoffgerüst eines Moleküls direkt beobachtet werden. Das Hauptproblem der 13C-NMR-S. ist die im Vergleich zur 1H-NMR-S. geringe Empfindlichkeit dieser Methode, da das magnetische Moment der 13C-Kerne kleiner als das der 1H-Kerne ist (der 13C-Kern weist nach Tab. 1 ein um etwa den Faktor 4 kleineres gyromagnetisches Verhältnis als der 1H-Kern auf) und die Häufigkeit von 13C im natürlichen Kohlenstoffisotopengemisch nur 1,1 % beträgt. Die Berücksichtigung beider Faktoren führt zu einem Empfindlichkeitsabfall um etwa 5000 bis 6000 gegenüber der 1H-NMR-S. Eine routinemäßige Messung von 13C-NMR-Spektren in natürlicher Häufigkeit wurde deshalb erst dann möglich, als durch meßtechnische Fortschritte die Nachweisempfindlichkeit der NMR-Spektrometer wesentlich erhöht wurde. Unter Empfindlichkeit versteht man das Verhältnis von Signalstärke S zum Rauschpegel N. Die wichtigsten zur Empfindlichkeitssteigerung angewandten Methoden sind: 1) Vergrößerung des Probenvolumens gegenüber der 1H-NMR-S. 2) Verwendung supraleitender Magnete, die eine hohe Feldstärke aufweisen. 3) Spektrenakkumulation, d. h., ein mit dem Spektrometer gekoppelter Computer addiert die durch wiederholtes Registrieren erhaltenen Spektren, wobei sich das Rauschen herausmittelt, während sich die Signale der Probe verstärken. Das Signal/Rausch-Verhältnis verbessert sich dabei mit der Quadratwurzel aus der Anzahl der Registrierungen n:
4) Puls-Fourier-Transform-(PFT-)Technik (Abb. 13). Mit einem kurzen Hochfrequenz-(HF-)Impuls (Impulsdauer ≈ 10-6 s) sehr hoher Intensität werden gleichzeitig alle 13C-Kerne angeregt, was mit einer Magnetisierung der Probe verbunden ist. Nach Abschalten des HF-Impulses kehren die Kerne in den Gleichgewichtszustand entsprechend der Boltzmann-Verteilung zurück, und man mißt den dabei einsetzenden Abfall der induzierten Magnetisierung [engl. free induction decay, Abk. FID] mit der Zeit. Im FID sind die gesamten Informationen eines konventionellen Spektrums enthalten, wenn auch in einer anderen Form. In jedem Teil des FID sind Informationen über das gesamte Spektrum vorhanden. Durch eine mathematische Operation, die Fourier-Transformation, ist es möglich, das Interferogramm, in dem der Abfall der induzierten Magnetisierung gegen die Zeit aufgetragen ist, in ein übliches Frequenzspektrum zu transformieren. Die Transformation geschieht mit einem direkt mit dem Spektrometer gekoppelten Computer. Da der Zeitbedarf für einen Impuls mit anschließender Aufzeichnung des FID sehr kurz ist, können mit Hilfe des Computers erst eine Reihe von Interferogrammen akkumuliert werden, ehe eine Fourier-Transformation durchgeführt wird. Der geringe Zeitbedarf ermöglicht somit eine gesteigerte Spektrenakkumulation und trägt wesentlich zu einer angestrebten Erhöhung der Empfindlichkeit bei.

NMR-Spektroskopie. Abb. 13: Blockschema eines Puls-Fourier-Transform-Spektrometers.
Besonderheiten der 13C-NMR-S. Aus einem 13C-NMR-Spektrum lassen sich wie aus einem 1H-NMR-Spektrum die in Tab. 2 verzeichneten Spektrenparameter entnehmen. Besonderheiten finden sich jedoch 1) bei der Anzahl der Signalgruppen und der chemischen Verschiebung: Der 13C-Resonanzbereich (etwa 0 bis 300 ppm) ist wesentlich größer als der Erwartungsbereich der 1H-Kerne (0 bis 10 ppm). Als Folge davon ergeben bereits geringe Unterschiede im Bindungszustand der einzelnen C-Atome zu deutlich getrennten Signalen Anlaß, und Überlappungen von Signalen, wie sie häufig im 1H-NMR-Spektrum auftreten, sind selten. Beispiel: Vom Vitamin B12 werden 59 verschiedene Resonanzfrequenzen beobachtet, die 59 nicht äquivalenten C-Atomen entsprechen. Die Erwartungsbereiche der 13C-chemischen Verschiebungen unterschiedlich gebundener C-Atome (Tab. 3) erlauben Aussagen über die Struktur der Probe.
2) bei den Signalintensitäten: Diese sind in den routinemäßig vermessenen 13C-NMR-Spektren nicht immer der Anzahl der Kerne proportional. Insbesondere quartäre C-Atome erscheinen oft mit verminderter Intensität.
3) bei der Multiplizität und den Kopplungskonstanten: Aufgrund der geringen natürlichen Häufigkeit des 13C-Isotops treten homonucleare 13C-13C-Kopplungen in Routinespektren nicht auf, da die Wahrscheinlichkeit sehr gering ist, daß zwei
13C-Kerne benachbart sind. Dagegen führen die heteronuclearen Kopplungen zwischen 13C und 1H (oder anderen magnetisch aktiven Kernen, wie 15N, 19F, 31P) zu starken Multiplettaufspaltungen. Die Kopplungskonstanten JC,H sind dabei mit Werten bis 300 Hz wesentlich größer als in der 1H-NMR-S. Diese Kopplungen machen das 13C-NMR-Spektrum sehr komplex. Durch die bereits erwähnte Protonen-Rauschentkopplung können sie eliminiert werden. Die meisten 13C-NMR-Spektren werden als rauschentkoppelte Spektren registriert, in denen für jeden 13C-Kern ein Singulett erscheint (Abb. 14a).
NMR-Spektroskopie. Tab. 3: Typische Erwartungsbereiche der 13C-chemischen Verschiebungen (in ppm gegen TMS).
| |||
| Alkine | 70 ... 90 | ||
| Alkene | 80 ... 150 | ||
| Aromaten | 110 ... 160 | ||
| Carbonylverbindungen | 160 ... 230 | ||
| Carboniumionen | 150 ... 300 |

NMR-Spektroskopie.Abb. 14: 13C-NMR-Spektrum von Isobutanol: (a) rauschentkoppelt, (b) off-resonance-Spektrum.
Durch die Unterdrückung der 13C-1H-Kopplungen werden allerdings auch wertvolle spektrale Informationen eliminiert. So ergeben im gekoppelten Spektrum die 13C-Signale einer CH3-Gruppe durch Kopplung mit 3 gebundenen H-Kernen ein Quartett, einer CH2-Gruppe ein Triplett, einer CH-Gruppe ein Dublett und eines quartären C-Atoms ein Singulett, was für ihre Zuordnung von großer Wichtigkeit ist. Mit der Methode der "off-resonance" können diese Informationen teilweise zurückgewonnen werden. Bei der off-resonance-Technik strahlt man außerhalb der Protonenresonanzfrequenzen großer Amplitude eine feste Frequenz ein. Unter diesen Bedingungen sind die 13C-1H-Kopplungen im Gegensatz zur Rauschentkopplung beobachtbar. Sie verkleinern sich allerdings im Vergleich zum nicht entkoppelten Spektrum erheblich (auf etwa 10 bis 50 Hz). Damit werden die Überlappungen benachbarter Multipletts weitgehend ausgeschaltet, und es entsteht ein übersichtliches Spektrum intensiver Multipletts erster Ordnung (Abb. 14b).
Übersicht über Anwendungsmöglichkeiten derNMR-S.Das wichtigste Anwendungsgebiet der NMR-S. ist gegenwärtig die Strukturaufklärung, insbesondere organischer Verbindungen. Mit Hilfe der aufgeführten Spektrenparameter lassen sich häufig detaillierte Aussagen über Anwesenheit und Anzahl bestimmter Atomgruppierungen machen sowie Nachbarschaftsbeziehungen ableiten. Im Falle der chemischen Verschiebung und der Kopplungskonstanten erfolgt dies durch Vergleich mit empirisch aufgestellten Zuordnungstabellen. Aus der Anzahl der Signale, der Intensität und der Multiplizität lassen sich unmittelbar, d. h. ohne Vergleichsmaterial, Strukturaussagen gewinnen. Eine vollständige Strukturanalyse aus dem NMR-Spektrum allein kann jedoch im allg. nicht erhalten werden. Sie bedarf der Kombination mit anderen Informationen, wie Elementaranalyse, Molekülmassebestimmungen, chem. Reaktivität, IR-, UV- und Massespektrum. Besondere Bedeutung hat die NMR-S. für Strukturuntersuchungen an Hochpolymeren, an denen Aussagen über Taktizität, Sequenzfolgen, cis/trans-Anordnung u. a. erhalten werden können. In jüngster Zeit konnte die NMR-S. zur Lösung zahlreicher biochemischer Fragestellungen herangezogen werden. Mit einer speziellen Technik (topical magnetic resonance) können Untersuchungen am lebenden Organismus durchgeführt und einzelne Organe (z. B. die Leber) selektiv vermessen werden. Infolge der zentralen Rolle und relativ hohen Konzentration von Adenosintriphosphat im lebenden Gewebe haben 31P-NMR-Messungen große Bedeutung. Quantitative Analyse: Grundlage der quantitativen Bestimmungen ist die Proportionalität zwischen Signalintensität und Anzahl der Kerne, die das Signal bewirken. Lassen sich in einer Mischung den einzelnen Komponenten eindeutig bestimmte Signale zuordnen, so kann aus dem NMR-Spektrum unmittelbar das Molverhältnis der Bestandteile angegeben werden, wobei berücksichtigt werden muß, wieviele Kerne das betreffende Analysensignal hervorbringt. Weiter muß berücksichtigt werden, daß die Intensität der Signale nicht durch unterschiedliche Relaxationszeiten oder den Kern-Overhauser-Effekt verfälscht werden. Durch Zusatz von Relaxationsreagenzien, z. B. paramagnetische Komplexe, wie Eisentrisactylacetonat, können diese Effekte weitgehend eliminiert werden. Große Bedeutung haben quantitative NMR-Untersuchungen für die Isotopenanalyse, insbesondere zur Bestimmung des Deuteriumgehalts. Sehr erfolgreich sind NMR-Messungen zur Untersuchung dynamischer Prozesse, wie inter- oder intramolekulare Bewegungen oder Austauschprozesse, die Aktivierungsenergien zwischen etwa 20 bis 100 kJ/mol erfordern, angewandt worden. Solche Prozesse sind z. B. Umlagerungen in Tautomeren, Konformationsumwandlungen, Valenzisomerisierungen, gehemmte innere Molekülrotationen oder Stickstoffinversionen. In einem dynamischen Prozeß A ![]()
B sei die chem. Umgebung eines Kerns in der Komponente A eine andere als in B. Ist die mittlere Aufenthaltsdauer des Kerns in jeder Umgebung groß gegenüber der Zeit, die für die Umorientierung des Kernspins notwendig ist (≈ 10-3 s), so erhält man dafür 2 scharfe getrennte Signale (Abb. 15a). Ist die mittlere Aufenthaltsdauer jedoch klein im Vergleich zu dieser Übergangszeit, so wechselt die chemische Umgebung des Kerns während des Umklappvorgangs. Im Spektrum verschmelzen die beiden Signale zu einem scharfen Signal (Abb. 15d). Die dafür beobachtete chemische Verschiebung wird von der durchschnittlichen chemischen Umgebung des Kerns bestimmt. Bei mittleren Aufenthaltsdauern erscheinen entweder ein oder zwei breite Signale (Abb. 15b und c). Man bezeichnet einen dynamischen Prozeß in der NMR-Zeitskale als langsam, wenn man im Spektrum zwei getrennte Signale erkennen kann, als schnell, wenn nur ein gemitteltes Signal erhalten wird. Da die Geschwindigkeit dynamischer Prozesse durch die Temperatur beeinflußt werden kann, werden NMR-Messungen bei verschiedenen Temperaturen durchgeführt. Die NMR-S. erlaubt zwei grundsätzliche Aussagen zu dynamischen Prozessen: 1) Bestimmung der Konzentration der im Gleichgewicht befindlichen Komponenten und 2) Bestimmung der kritischen Parameter des Prozesses in Form der Geschwindigkeitskonstanten und der Aktivierungsenergie bzw. der freien Aktivierungsenthalpie.
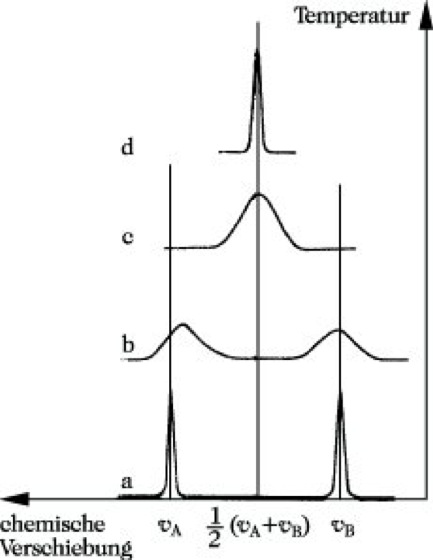
NMR-Spektroskopie. Abb. 15: Änderung der Bandenform in Abhängigkeit von der Austauschgeschwindigkeit.
II) Breitband-NMR-S. Gegenüber der NMR-S. in Flüssigkeiten treten bei der Untersuchung von Festkörpern wegen ihres anderen Aggregatzustandes zwei wesentliche Besonderheiten auf: 1) Dipol-, Quadrupol- und andere Wechselwirkungen, die in Flüssigkeiten durch die Bewegung der Moleküle ausgemittelt werden, bestimmen in vielen Fällen die Linienformen und das Spektrum. 2) Die Anisotropie der Wechselwirkungen führt zu einer Abhängigkeit des Spektrums von der Orientierung der Probe im äußeren Magnetfeld. Dies führt dazu, daß im Gegensatz zu gelösten Stoffen in Festkörpern die Linien wesentlich breiter und außerdem winkelabhängig sein können. Chemische Verschiebungen und Multiplizitäten können deshalb im allg. nicht beobachtet werden. Dagegen lassen sich Kernabstände und ihre Winkellage im Kristall erhalten. Dies hat vor allem für die Ermittlung von Protonenabständen in wasserstoffenthaltenden Kristallen Bedeutung, da wegen der geringen Beugung von Röntgenstrahlen diese leichten Kerne mit Hilfe der Röntgen-(Kristall-)strukturanalyse nicht ermittelt werden können. Auf diese Weise wurden aufschlußreiche Informationen über die Detailstrukturen solcher Systeme erhalten. Für manche Festkörper zeigt die Linienbreite eine plötzliche Schmälerung, wenn die Temperatur über eine bestimmte Grenze hinaus gesteigert wird. Dies weist auf das Einsetzen bestimmter molekularer Bewegungsvorgänge hin, wodurch sich die Wechselwirkungen mit Nachbaratomen größtenteils auslöschen.
Durch spezielle Techniken ist es möglich, die sonst dominierenden Dipolwechselwirkungen zu unterdrücken, so daß hochaufgelöste Spektren erhalten werden (Festkörperhochauflösung).
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.