Lexikon der Chemie: Reaktionskinetik
Reaktionskinetik, chemische Kinetik, Teildisziplin der physikalischen Chemie, die den zeitlichen Ablauf chem. Reaktionen experimentell untersucht (kinetische Methoden), mathematisch beschreibt (Formalkinetik) und theoretisch begründet (theoretische R.). Die R. liefert Beiträge zur Aufklärung und zum Verständnis von Reaktionsmechanismen. Sie unterscheidet Elementarreaktion und komplexe Reaktion. Die R. bildet eine wichtige Grundlage der chem. Verfahrenstechnik. Reaktionskinetische und thermodynamische Daten sind gemeinsam mit Transportgrößen (Diffusion, Wärmeleitung, Hydrodynamik) die Basis zur Berechnung und Optimierung technischer Reaktoren.
Ein zentraler Begriff der R. ist die Reaktionsgeschwindigkeit r. Sie gibt an, wie schnell die verschiedenen Komponenten A, B, C, D ... eines nicht im Gleichgewicht befindlichen Systems dem chem. Gleichgewicht (Gleichgewicht 3) zustreben. Läuft die Reaktion |νA| A + |νB|B + ... → νCC + νDD + ... ab, so ist die Reaktionsgeschwindigkeit definiert als 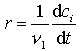
. Hierbei sind νi stöchiometrische Faktoren, die für Ausgangsstoffe negatives Vorzeichen und für Produkte positives Vorzeichen haben, ci die Konzentration der Komponenten i und t die Zeit.

Reaktionskinetik. Tab.: Einfache kinetische Zeitgesetze und Halbwertszeiten (für den Fall|νi|=±1).
a) Halbwertszeit für den Reaktanten 1
b) Halbwertszeit für den Reaktanten 2
Die Reaktionsgeschwindigkeit ist abhängig von den Konzentrationen der Reaktanten, von Katalysatoren, der Art des Lösungsmittels, der Temperatur, dem Druck, der Größe der Grenzfläche bei heterogenen Reaktionen u. a. Die Funktion r = f(ci) bei Konstanz aller übrigen Parameter wird als kinetisches Zeitgesetz (Geschwindigkeitsgleichung) bezeichnet. Vollständig verlaufende Reaktionen werden häufig durch einfache Zeitgesetze in Potenzform
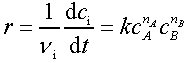
gut beschrieben. Die Summe der Exponenten Σni = n wird als Reaktionsordnung bezeichnet, der Proportionalitätsfaktor k als Geschwindigkeitskonstante. Aus theoretischen Modellvorstellungen folgt, daß für Elementarreaktionen die Reaktionsordnungen ni kleine natürliche Zahlen sind, die mit den Stöchiometriefaktoren |νi| der Reaktionsgleichung übereinstimmen (s. u.). Dagegen müssen in Zeitgesetzen für komplexe Reaktionen die Reaktionsordnungen nicht mit den Stöchiometriezahlen übereinstimmen. Es können nicht ganzzahlige Ordnungen auftreten oder Zeitgesetze, die keine Potenzfunktionen darstellen und für die sich deshalb eine Reaktionsordnung nicht definieren läßt.
Durch Integration der Zeitgesetze erhält man Funktionen ci = f(t), die den experimentell meßbaren Konzentrations-Zeit-Verlauf explizit beschreiben (Abb.). Gehorcht z. B. die Reaktion einem Zeitgesetz 1. Ordnung bezüglich des Stoffes A gemäß
Als Halbwertszeit t1/2 bezeichnet man die Reaktionszeit, nach der die Hälfte der Anfangsmenge verbraucht ist, d. h., es gilt ci = 1/2 ci0 (Halbwertszeit).
In der Tab. sind die einfachen kinetischen Zeitgesetze und Halbwertszeiten zusammengestellt.
Die Geschwindigkeit chem. Reaktionen wächst im allg. stark mit der Temperatur (Arrhenius-Gleichung).
Experimentelle Methoden. Reaktionskinetische Messungen erfordern die Bestimmung der zeitlichen Konzentrationsänderungen der Ausgangs- und Endstoffe und möglichst auch der Zwischenprodukte. Für relativ langsam ablaufende Reaktionen (> 102 s) eignen sich statische Methoden, bei denen sich das Reaktionsgemisch bei konstanter Temperatur in einem Reaktor befindet und der Umsatz durch Probenahme oder innerhalb der Mischung analytisch verfolgt wird. Bei schnelleren Vorgängen (102 bis 10-3 s) werden Stoffströme der Komponenten unmittelbar vor dem Reaktionsraum vermischt, strömen durch diesen hindurch und werden nach dem Austritt analysiert (Strömungsmethoden). Bei der Stopped-flow-Methode (besonders geeignet für kleine Probenvolumina) preßt man die vermischten Reaktanten in ein Strömungsrohr; ist ein bestimmtes Volumen injiziert, so stoppt ein Kolben die Strömung, und die Reaktion wird in der ruhenden Mischung weiterverfolgt. Sehr schnelle Prozesse können nicht mehr durch Vermischen der Ausgangsstoffe studiert werden, da die Mischzeiten mindestens in der Größenordnung von 10-3 s liegen. Deshalb wendet man Verfahren an, bei denen das Gleichgewicht durch eine sprunghafte, pulsartige oder periodische Störung eines äußeren Parameters (z. B. Temperatur, Druck) gestört wird. Mit einem schnellen Analysenverfahren wird verfolgt, wie sich in dem System verzögert die neue Gleichgewichtslage einstellt. Werden sehr kleine Störungen verwendet, spricht man von Relaxationsmethoden. Mit großen Störungen arbeiten z. B. die Blitzlichtphotolyse, die Pulsradiolyse und das Stoßverfahren.
Bei der Blitzlichtphotolyse werden in einer Meßzelle durch einen starken Lichtblitz hohe Konzentrationen photochemisch angeregter oder gespaltener Spezies erzeugt. Ihre Folgeprozesse werden mit Hilfe einer schnell registrierenden photochem. Meßanordnung studiert. Besonders kurze Blitzzeiten bis in den Femtosekundenbereich sind mit Lasern möglich (Laserblitzphotolyse). Verwendet man anstelle von Licht energiereiche Strahlung (z. B. Elektronenstrahlung aus einem Beschleuniger), bezeichnet man die Methode als Pulsradiolyse. Beim Stoßrohrverfahren läßt man eine sehr steile Druckwelle in das Reaktionsmedium laufen. Durch die starke adiabatische Aufheizung (bis auf mehrere tausend Kelvin) werden schnelle thermische Reaktionen ausgelöst, die senkrecht zur Richtung der Druckwelle meßtechnisch verfolgt werden können.
Theorie. Die theoretische R. verfolgt das Ziel, den detaillierten Ablauf von Elementarreaktionen auf molekularer Grundlage zu interpretieren, die Form der geltenden Zeitgesetze zu begründen und die Geschwindigkeitskonstanten zu berechnen. Sie geht von folgenden Modellvorstellungen aus: a) Voraussetzung für den Ablauf einer makroskopischen chem. Elementarreaktion ist eine Vielzahl mikrophysikalischer Elementarprozesse. Die Teilchen müssen zusammenstoßen, wobei nichtreaktive und reaktive Stöße möglich sind. Bei nichtreaktiven Stößen finden nur ein Energieaustausch und eine Richtungsänderung statt. b) Reaktive Stöße erfordern meistens die Überwindung einer Potentialbarriere, da sich die Teilchen der Ausgangs- und Endstoffe auf der Potentialfläche in Minima befinden, die durch Gebiete mit höherer potentieller Energie voneinander getrennt sind. Ursache ist das Auftreten von Abstoßungskräften, wenn zwei Teilchen sich einander nähern. Die Höhe der Potentialschwelle wird Schwellenenergie E0 genannt. Sie liegt im allg. zwischen 20 und 40 kJ mol-1. Es gibt auch Reaktionen ohne Potentialschwelle (E0 ≈ 0), z. B. die Kombination von zwei Radikalen oder entgegengesetzt geladenen Ionen sowie eine Reihe von Ionen-Molekül-Reaktionen. Die Existenz der Potentialbarriere erfordert, daß ein Teilchenpaar beim Zusammenstoß über eine Relativenergie (einschließlich der Energiebeiträge aus den inneren Freiheitsgraden) verfügen muß, die größer oder gleich der Schwellenenergie ist, damit der Stoß reaktiv sein kann. Außerdem muß die räumliche Orientierung im Stoßkomplex die Bindungsumlagerung ermöglichen. c) Für die meisten chem. Reaktionen (Ausnahme: sehr schnelle Vorgänge) ist die Anzahl der nichtreaktiven Stöße sehr groß im Vergleich zu den reaktiven Stößen. Dadurch ist eine regellose homogene Verteilung der Teilchen im Raum gewährleistet, und ihre Energien unterliegen einer Gleichgewichtsverteilung. Darauf basierende Konzepte der theoretischen R. bezeichnet man als Gleichgewichtstheorien.
Ausgehend von diesen Grundvorstellungen sind zahlreiche theoretische Ansätze mit unterschiedlichem Grad der Vereinfachung und Verallgemeinerung der Modelle entwickelt worden:
1) Die einfache Stoßtheorie basiert auf den Vorstellungen der kinetischen Gastheorie. Sie berechnet die Anzahl der Stöße der reagierenden Teilchen. Der Bruchteil der Stöße mit einer Relativenergie ≥ E0 wird durch den Boltzmann-Faktor exp(-E0/RT) berücksichtigt. Die wichtigsten Resultate sind: a) Für mono-, bi- und trimolekulare Elementarreaktionen gelten Zeitgesetze 1., 2. bzw. 3. Ordnung. Dabei erfordern monomolekulare Reaktionen gesonderte Überlegungen. b) Für die 1eschwindigkeitskonstante liefert die Stoßtheorie k = PBT1/2 exp(-E0/RT). Für eine bimolekulare Reaktion A + B → Produkte ist die Konstante B gegeben durch B = σ(8 RT/πμ)1/2NA, wobei R die Gaskonstante, T Kelvin-Temperatur, NA Avogadro-Konstante und μ = MAMB/(MA + MB) die reduzierte molare Masse von A und B bedeuten. σ = (rA+ rB)2π ist der Stoßquerschnitt, d. i. die Fläche, innerhalb derer zwei aufeinander zufliegende kugelförmige Teilchen A und B mit den Radien rA und rB zusammenstoßen oder sich zumindest streifend berühren. P wird als sterischer Faktor bezeichnet. Er soll als Korrekturfaktor den Bruchteil der Stöße angeben, bei denen reale nicht kugelförmige Teilchen räumlich so orientiert sind, daß die Bindungsumlagerung möglich ist. Er kann folglich nur positive Werte ≤ 1 annehmen. Für viele Gasreaktionen liefert die obige Beziehung Geschwindigkeitskonstanten in der richtigen Größenordnung, wenn P = 1 gesetzt wird. Dagegen treten aber auch große Abweichungen auf. Die Beziehung für die Geschwindigkeitskonstante ähnelt sehr stark der empirischen Arrhenius-Gleichung, wobei PBT1/2 ≈ A und E0 ≈ EA entspricht (A ist der Frequenzfaktor, EA die Arrheniussche Aktivierungsenergie).
2) Eine allgemeinere Behandlung bimolekularer Reaktionen und nichtreaktiver Stoßprozesse in verd. Gasen ist mit Hilfe der Boltzmannschen Stoßgleichung möglich. Nach einer Reihe von Vereinfachungen liefert sie für die Geschwindigkeitskonstante den Ausdruck k = ∫∫ vσR fA(vA) fB(vB) dvA dvB. Dabei ist v = vA – vB die Differenz der vektoriellen Geschwindigkeiten der Reaktanten A und B, fA(vA) und fB(vB) sind deren Verteilungsfunktionen. σR ist der reaktive Streu- oder Reaktionsquerschnitt der beiden Reaktanten. Er ist in Analogie zum Stoßquerschnitt als eine effektive Fläche aufzufassen, die ein Teilchen A dem stoßenden Teilchen B darbietet. Erfolgt die Teilchenbegegnung innerhalb dieser Fläche, so ist der Stoß reaktiv. Da der Reaktionsquerschnitt auch die energetischen Bedingungen des Stoßvorganges, insbesondere die Existenz einer Potentialschwelle enthält, ist er abhängig von der Energie der stoßenden Teilchen und im allg. wesentlich kleiner als der geometrisch definierte Stoßquerschnitt. Streuquerschnitte können mit gekreuzten Molekularstrahlen experimentell bestimmt oder durch Modellansätze oder Trajektorienrechnungen (s. u.) berechnet werden.
3) Einen genaueren Einblick in die Bewegungen eines zusammenstoßenden Teilchenpaares liefern Trajektorienrechnungen. Als Trajektorie bezeichnet man die zeitliche Änderung des Abstandes eines zusammenstoßenden Teilchenpaares unter dem Einfluß des Wechselwirkungspotentials. Bildlich entspricht das der Bahnkurve eines Punktes auf der Potentialfläche, die aus quantenchem. Rechnungen bekannt sein muß. Für die Bewegung wird die Gültigkeit der klassischen Mechanik vorausgesetzt. Man gibt für das stoßende Teilchenpaar die genauen Anfangsbedingungen, d. h. die Relativenergie der Translation und die innere Bewegungsrichtung vor und löst schrittweise die Bewegungsgleichungen der klassischen Mechanik. Als Ergebnis erhält man Aussagen über Änderungen der Bindungsabstände auf der Bahnkurve, das Auftreten eines reaktiven oder nichtreaktiven Stoßes und die Anregungszustände der Teilchen nach der Wechselwirkung. Durch Mittelung über eine Vielzahl derartiger Rechnungen (im allg. einige hundert bis tausend) erhält man die Reaktionswahrscheinlichkeit P = ΔNR/N (wobei N Anzahl der berechneten Teilchenpaare, ΔNR Anzahl der reaktiven Stöße) und den Reaktionsquerschnitt σR = Pσ = P(rA + rR)2π.
4) Die zur Zeit tragfähigste Theorie des Reaktionsablaufes ist die Eyringsche Theorie (Theorie des Übergangszustandes, Abk. TÜZ, Theorie des aktivierten Komplexes). Die TÜZ betrachtet den Stoßkomplex im Maximum der Potentialbarriere als eine besondere Konfiguration und bezeichnet diese als Übergangszustand (aktivierter Komplex). Dieser Stoßkomplex soll über eine Lebensdauer von einigen wenigen Schwingungsperioden (Größenordnung 10-12 s) verfügen, die dazu ausreicht, daß sich eine Gleichgewichtsverteilung der Energie zwischen den inneren Freiheitsgraden einstellen kann. Weitere Annahmen sind: a) Für den Übergangszustand lassen sich thermodynamische Funktionen definieren. b) Der Übergangszustand steht im Gleichgewicht mit den Ausgangsstoffen, d. h., es gilt das Reaktionsschema AB + C ![]()
[A ... B ... C] =| → A + BC, wobei [A ... B ... C] =| den Übergangszustand bezeichnet. c) Die Reaktionsgeschwindigkeit ist proportional der Konzentration der aktivierten Komplexe. Der Proportionalitätsfaktor ν=| = kBT/h folgt aus dem Postulat, daß ein Schwingungsfreiheitsgrad, nämlich der entlang der Reaktionskoordinate, den Charakter einer Translation annimmt, die zur Spaltung der alten und Bildung der neuen Bindung führt. kB ist die Boltzmann-Konstante, T die absolute Temperatur und h das Plancksche Wirkungsquantum. Aus c) folgt r = (kBT/h)c=|, wobei c=| die Konzentration der Übergangszustände bezeichnet, die aus dem Massenwirkungsgesetz (Annahme b) zugänglich ist: K=| = c=|/(cABcC). Man erhält r = (kBT/h)K=|cABcC, d. h. ein Zeitgesetz 2. Ordnung für das angeführte Beispiel einer bimolekularen Reaktion. Die Anwendung auf mono- und trimolekulare Reaktionen ergibt (analog zur einfachen Stoßtheorie) Zeitgesetze 1. bzw. 3. Ordnung.
Der Faktor (kBT/h)K=| = k entspricht dabei der makroskopischen Geschwindigkeitskonstanten k. Der Zugang zu den Gleichgewichtskonstanten K=| ist auf zwei Wegen möglich. Mit Hilfe der Beziehungen der phänomenologischen Thermodynamik
ΔG=| = – RT ln K=| und ΔG=| = ΔH=| – TΔS=|
erhält man für die Geschwindigkeitskonstante k = (kBT/h)eΔS =| /R e-ΔH =| /RT (Eyring-Gleichung). Hierbei sind ΔS=| die Aktivierungsentropie und ΔH=| die Aktivierungsenthalpie. Außerdem kann K=| mit Hilfe der Zustandssummen der statistischen Thermodynamik formuliert werden. Für eine bimolekulare Reaktion ergibt sich
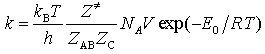
.
Dabei sind Z=|, ZAB und ZC die Zustandssummen des aktivierten. Komplexes und der Ausgangsstoffe AB und C. NA ist die Avogadro-Konstante und V das Volumen der Reaktionsmischung. E0 ist die molare Differenz der Nullpunktsenergien zwischen dem Übergangszustand und den Ausgangsstoffen und entspricht der Höhe der Potentialschwelle. Ist die Geometrie des Übergangszustandes bekannt (z. B. aus quantenchem. Berechnungen), so sind die Zustandssummen aus den Moleküldaten der drei Komponenten berechenbar. Dabei ist zu beachten, daß aus Z=| ein Freiheitsgrad der Schwingung entlang der Reaktionskoordinate abgespalten wurde, um die Zerfallsfrequenz ν=| = kBT/h festzulegen.
5) Auf Reaktionen in Lösung sind prinzipiell die gleichen Vorstellungen anwendbar. Wichtiger Unterschied ist die wesentlich höhere Teilchendichte. Das hat vor allem zwei Konsequenzen: a) Der Transport der reagierenden Teilchen zueinander ist erschwert. Bei vielen Reaktionen bestimmt er die Reaktionsgeschwindigkeit (Diffusionskontrolle). b) Zwischen den Molekülen des Lösungsmittels und der Reaktanten treten starke Wechselwirkungen, vor allem Solvatationen auf, die die energetischen Verhältnisse ändern. In der Theorie des Übergangszustandes lassen sich diese dadurch berücksichtigen, daß man das Gleichgewicht zwischen aktiviertem Komplex und den Ausgangsstoffen mit Aktivitäten anstelle der Konzentrationen formuliert. Dann ergibt sich für die Eyring-Gleichung
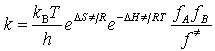
,
wobei fA, fB und f =| die Aktivitätskoeffizienten der Ausgangsstoffe A und B und des Übergangszustandes bezeichnen. Sind die Wechselwirkungen der Reaktanten größer als die des Übergangszustandes, ist (fA fB/f =|) < 1, d. h., die Reaktion wird verzögert, im entgegengesetzten Fall beschleunigt (Ingold-Regel).
6) Makroskopische Aussagen zur theoretischen R. liefert die nichtlineare Theorie irreversibler Prozesse (Thermodynamik).
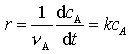

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.