Zustandssumme (Symbol Z oder Q), eine zentrale Größe in der statistischen Thermodynamik, die angibt, wie sich die Gesamtenergie eines Moleküls auf seine verschiedenen Freiheitsgrade verteilen

kann. Sie ist definiert durch die Beziehung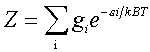

, wobei k_B die Boltzmann-Konstante, T

die absolute Temperatur, ε_i einen definierten Energiezustand i und g_i die Anzahl der Zustände mit gleicher Energie (Energieentartung) angibt. Die Summation erfolgt über alle Energiezustände. Mit Hilfe der Z. ist die Berechnung makroskopischer thermodynamischer Zustandsgrößen aus Moleküldaten möglich. So gelten z. B. folgende Zusammenhänge: U = RT²(d ln Z/dT); S = R ln Z + RT(d ln Z/dT) und F = -RT ln Z. Unter der Voraussetzung, daß sich die Gesamtenergie ε₁ eines Moleküls additiv aus den Energiebeiträgen zusammensetzt, die in seinen einzelnen Freiheitsgraden gespeichert sind, ε₁ = ε_trans + ε_rot + ε_schw + ε_e1 + ε_Kern, läßt sich die e-Funktion der Z. in ein Produkt von e-Funktionen und damit in Teilzustandssummen für diese verschiedenen Freiheitsgrade aufspalten: Z = Z_trans·Z_rot·Z_schw·Z_el·Z_Kern. Für diese Teilzustandssummen gelten folgende Beziehungen: Zustandssumme Z_trans für 3 Translationsfreiheitsgrade:

Z_trans = h^-3(2πmk_BT)^3/2V mit h = Plancksche Konstante, m = Molekülmasse, V = Volumen des Gases; Zustandssumme Z_rot der Rotation des Moleküls: Z_rot = h^-2σ^-1(8π²Ik_BT) für lineare Moleküle und Z_rot = h^-3 σ^-1 π^1/2·(8 π²k_BT)^3/2(I_aI_bI_c)^1/2 für nichtlineare Moleküle mit σ = Symmetriezahl (Zahl der Deckungsoperationen bei einer Drehung um 360°), I = Hauptträgheitsmoment des linearen Moleküls, I_a, I_b, I_c = Trägheitsmomente bezüglich der drei Drehachsen des Moleküls; Zustandssumme Z_schw der Schwingung:

mit j = Numerierung der 3 N – 6 Schwingungsfreiheitsgrade und u_j = hν_j/k_BT, wobei ν_j die Schwingungsfrequenz der j-ten Normalschwingung bezeichnet. Lineare Moleküle verfügen über 3 N – 5 Schwingungsfreiheitsgrade, so daß für sie j von 1 bis 3 N – 5 läuft.

Chem. Reaktionen verlaufen ohne Änderung der Kernzustände, thermische Vorgänge im allg. im elektronischen Grundzustand, so daß Z_Kern und Z_el keinen Einfluß auf die gesamte Z. haben und deshalb Z_Kern = Z_el = 1 gesetzt werden. Damit ermöglicht die Kenntnis der Moleküldaten m, I und aller ν_j die Berechnung der Z. und damit thermodynamischer Zustandsgrößen und Gleichgewichte.