Lexikon der Geowissenschaften: elektromagnetische Verfahren
elektromagnetische Verfahren, EM-Verfahren, i.w.S. alle geophysikalischen Methoden, welche die Erkundung der elektrischen Leitfähigkeitsverteilung im Untergrund zum Ziel haben. Dabei werden elektrische und/oder magnetische Feldgrößen an der Erdoberfläche, im Bohrloch oder in der Luft gemessen. Die Anwendungsgebiete der elektromagnetischen Verfahren reichen von Aufgaben im Umweltbereich und der Erzexploration über geologisch-tektonische Fragestellungen bis hin zu Studien der tiefen Erdkruste und des oberen Erdmantels. Die gelegentlich schwer überschaubar wirkende Vielfalt an speziellen Methoden hat ihre Ursache in der Ausnutzung eines weiten Frequenzbereichs, der von f ≈ 0 Hz (z.B. Gleichstromgeoelektrik) bis zu einigen GHz (Bodenradar) reicht, und der Kombinationsmöglichkeit unterschiedlichster Sender-Empfänger-Anordnungen und damit Feldgeometrien (geoelektrische Verfahren).
Unter einem engeren Blickwinkel werden nur solche als EM-Verfahren bezeichnet, die den elektromagnetischen Skineffekt direkt ausnutzen; als solche nennt man sie auch Induktionsverfahren. Sie lassen sich noch einmal untergliedern in Frequenz- und Zeitbereichsverfahren; bei ersteren erhält man eine von der Leitfähigkeitsverteilung im Untergrund abhängige Übertragungsfunktion als Funktion der Frequenz, während man bei letzteren die endliche Abklingzeit elektromagnetischer Felder in elektrischen Leitern nach Abschalten einer Sendeeinrichtung untersucht (Transienten-Elektromagnetik). Im Frequenzbereich kennt man sowohl passive, d.h. rein beobachtende Verfahren – wobei das anregende Feld natürlichen Ursprungs ist (Magnetotellurik) bzw. von weit entfernten Sendern stammt, die primär anderen Zwecken dienen und lediglich für die geophysikalische Anwendung benutzt werden (VLF-Verfahren) –, als auch aktive Methoden, die den Betrieb eines eigenen Senders erfordern. Die Abgrenzung des Frequenzbereichs folgt aus den Maxwellschen Gleichungen:
∇´![]()
= ∂![]()
/∂t+![]()
(1)
∇´![]()
= -∂![]()
/∂t (2)
mit: ![]()
= magnetische Feldstärke, ![]()
= dielektrische Verschiebung, ![]()
= Stromdichte, ![]()
= elektrische Feldstärke und ![]()
= Induktionsflußdichte. Für sehr hohe Frequenzen überwiegt der Anteil des Verschiebungsstroms ∂D/∂t, der Leitungsstrom J kann vernachlässigt werden. Umgekehrt dominiert der Leitungsstrom bei niedrigen Frequenzen und im Extremfall der Gleichstromverfahren sind alle zeitlichen Ableitungen gleich 0. Aus (1) und (2) läßt sich die eindimensionale Helmholtz-Gleichung:
für die gedämpfte Ausbreitung einer elektromagnetischen Welle mit der Lösung
F(z) = F0exp(-γz) (4)
ableiten; dabei repräsentiert F die elektrische Feldstärke E oder die magnetische Induktionsflußdichte B mit einer zeitlichen Abhängigkeit proportional zu exp(iωt); t steht dabei für die Zeit und ω für die Kreisfrequenz; γ ist die komplexe Ausbreitungskonstante ("Wellenzahl") mit:
γ2 = ν2+iωμσ-μεω2 = ν2+k2-κ2. (5)
Dabei bezeichnet ν = 2π/l die laterale Wellenzahl, l ist die Wellenlänge und damit ein Maß für die Veränderlichkeit des Feldes in lateraler Raumrichtung (x, y). Der größte der Terme in (5) bestimmt wesentlich die Größe von γ und damit den Charakter des Feldes:
a) k > >ν, κ: Das Feld ist quasi-homogen (Fernfeldnäherung, die Felder verhalten sich ähnlich einer ebenen Welle) und der Leitungsstrom überwiegt gegenüber dem Verschiebungsstrom. Die Phasenvariation einer einfallenden ebenen Welle über einem Untersuchungsgebiet kann dabei vernachlässigt werden. Denn bei einer Frequenz von z.B. 1 kHz beträgt die Wellenlänge λ = c0/f = 105 m, bei 1 Hz ist λ = 108 m usw. (Lichtgeschwindigkeit c0 ≈ 3·108 m/s) und ist damit immer sehr viel größer als das betrachtete Target ( Abb. 1 ). Dies ist der Fall der Magnetotellurik, der erdmagnetischen Tiefensondierung und auch des VLF-Verfahrens bzw. VLF-R-Verfahrens. Das elektromagnetische Feld diffundiert in den elektrisch leitenden Untergrund; es wird gedämpft und ist in der Skintiefe (Eindringtiefe)
auf den 1/e-ten Teil seines Wertes an der Oberfläche abgefallen; dabei erfährt es auch eine Phasenverschiebung, die 1 rad in der Tiefe z = δ beträgt. Im Zeitbereich entsprechen die späten Zeiten der Fernfeldnäherung und
ist analog der Tiefe, bis in die das Feld zu einem Zeitpunkt t nach Abschalten eines Magnetfeldes diffundiert ist.
b) ν > >k, κ: Bei sehr niederfrequenter Anregung durch eine stark inhomogene Quelle (der Beobachtungspunkt befindet sich im Nahfeld eines Sendedipols; die Gleichstromgeoelektrik stellt gewissermaßen einen Extremfall dar) wird γ ≈ ν, die Variation des Feldes also durch den nun rein geometrischen Term exp(-γz) bestimmt. Das bedeutet, je inhomogener das Feld in horizontaler Richtung ist, desto schneller klingt es mit der Tiefe z ab. Das Magnetfeld trägt in diesem Fall keine Information über die elektrische Leitfähigkeit des Untergrunds. Im Zeitbereich entspricht dieser Nahfeldbereich den frühen Zeiten nach Abschalten des Signals (Transienten).
c) κ > >ν, k: Bei hohen Frequenzen und ebenen Wellen erfolgt die Ausbreitung in einem schlechten Leiter ungedämpft. Dies ist der Fall des Geo- oder Bodenradars, wobei allerdings in der Praxis die Frequenzen nicht so hoch gewählt werden können, daß der Anteil von k völlig vernachlässigt werden kann.
Die Induktionsverfahren werden durch die Fälle a) und b) beschrieben, also einer Diffusion mit eventueller zusätzlicher geometrischer Dämpfung des Feldes. Diese bewirkt für die meisten aktiven Methoden, bei welchen der Abstand Sender-Empfänger häufig in der Größenordnung der Skintiefe liegt, eine geringere Eindringtiefe im Vergleich zu den Fernfeldmethoden in a) (Gleichung 6). Im Fernfeld eines Senders spielt die laterale Variation des Feldes keine Rolle mehr gegenüber der Eindringtiefe δ. Üblicherweise mißt man die Komponenten der magnetischen und auch – wie in der Magnetotellurik und im VLF-R-Verfahren – elektrischen Felder an der Erdoberfläche und bezieht sie aufeinander. Man berechnet Übertragungsfunktionen zwischen den Feldkomponenten, die Rückschlüsse auf die Leitfähigkeitsverteilung im Erdinnern erlauben. Die Stärke des Quellenfeldes spielt (bei ausreichendem Signal/Rausch-Verhältnis) keine Rolle. Da die Skintiefe von der Leitfähigkeit und der Frequenz abhängt, erreicht man durch Bestimmung der Übertragungsfunktionen bei verschiedenen Frequenzen eine Sondierung unterschiedlicher Tiefenbereiche. Im Nahfeld oder im Übergangsbereich Nahfeld/Fernfeld einer Quelle (z.B. eines magnetischen Dipols, der durch eine von einem elektrischen Wechselstrom der Frequenz ω durchflossenen Leiterschleife realisiert wird), ist die horizontale Variation des Feldes groß gegenüber bzw. vergleichbar der Wellenlänge λ im Untergrund. Daher muß hier das primäre Feld des Senders berücksichtigt werden. Dies erfordert die Berechnung des Feldes von magnetischen oder elektrischen Dipol- oder Linienquellen über einem leitfähigen Untergrund. Aufgrund des aufwendigen Formalismus wird häufig eine Wechselstromkreis-Analogie zur Erklärung des Anomalieverlaufs in den Frequenzbereichsmethoden gewählt. Dabei denkt man sich den im Vergleich zur Umgebung elektrisch besser leitfähigen Störkörper (dem Explorationsziel) im Untergrund durch eine Leiterschleife ersetzt. Das Wechselfeld des Sendedipols induziert in dieser Leiterschleife Wirbelströme, die wiederum ein sekundäres Magnetfeld Bs am Ort des Empfängers erzeugen ( Abb. 2 ). Bezieht man nun dieses Sekundärfeld auf das primäre Feld Bp, das ohne den "Umweg" über den Störkörper direkt vom Sender zum Empfänger gelangt, so erhält man einen charakteristischen Anomalieverlauf des Verhältnisses Bs/Bp als Funktion der Profilkoordinate x über den Störkörper. Die Darstellung erfolgt meist getrennt in Realteil (In-Phase) und Imaginärteil (Out-of-Phase, Quadratur) und in Prozent oder ppm des Primärfeldes. Formal ersetzt man den Störkörper somit durch eine Reihenschaltung ( Abb. 3 ) aus einem rein Ohmschen Widerstand R und einer Induktivität L mit einem resultierenden komplexen Widerstand Z = R+iωL. Das Verhältnis p = ωL/R (Induktionszahl) beschreibt den Anteil des induktiven Widerstandes gegenüber dem Gleichstromwiderstand R bei einer Frequenz ω. Ist Lij die Gegeninduktivität zwischen den Leiterschleifen mit der Induktivität Li bzw. Lj (also der Induktionsfluß, der in einer Leiterschleife j von einem Strom in der Schleife i hervorgerufen wird), so erhält man als Verhältnis aus sekundärer, vom Störkörper (L2) in der Empfängerspule (L3) induzierter Spannung U23 und vom Primärfeld (Induktivität des Senders L1) im Empfänger induzierter Spannung U13:

ΔU wird dann getrennt für Realteil (In-Phase) und Imaginärteil (Out-of-Phase) dargestellt. Der Kopplungskoeffizient K gibt das Verhältnis der magnetischen Flüsse an, die die Empfängerspule über den Untergrund bzw. direkt an die Senderspule ankoppeln. Während K nur von der Position und Größe der Leiterschleife im Untergrund abhängt, beschreibt die komplexwertige und dimensionslose Responsefunktion W(p) die elektrischen Eigenschaften des Untergrunds. Für große Induktionszahlen ist W(p→∞) = 1 und reell, d.h. an dieser sog. induktiven Grenze existiert kein Quadraturterm. Umgekehrt überwiegt der Imaginärteil bei kleinen Induktionszahlen (W(p)→ip) und ΔU = -iωK/R; die Antwort des Systems ist proportional zur Frequenz und die Phasenverschiebung beträgt -90°.
In den aktiven Frequenzbereichs-Verfahren wird eine Tiefensondierung der elektrischen Leitfähigkeitsverteilung sowohl durch eine Veränderung des Sender-Empfänger-Abstandes, als auch der Frequenz erreicht, woraus die große Vielfalt an Methoden resultiert. Wichtige Beispiele sind die Zweispulen-, und hier insbesondere das Slingram-Verfahren, das meist mit horizontalen, koplanaren Spulensystemen realisiert wird ( Abb. 4 , Abb. 5 ). Je nach Durchmesser der verwendeten Spulen und geforderter Erkundungstiefe werden Sender-Empfängerabstände von einigen m bis etwa 200 m gewählt; der Frequenzbereich liegt zwischen etwa 100 Hz und 60 kHz. Daher wird das Verfahren insbesondere in der oberflächennahen Exploration (z 100 m) eingesetzt. Da solche Systeme nur Magnetfelder messen, sind sie besonders für den Einsatz in der Aerogeophysik geeignet und ermöglichen damit eine schnelle und flächenhafte Kartierung eines Untersuchungsgebiets. Ein Nachteil der Zweispulen-Systeme ist ihre starke Abhängigkeit vom Sender-Empfänger-Abstand und auch von der Topographie des Untersuchungsgebietes.
Die Ergebnisse elektromagnetischer Messungen werden heute ausschließlich digital abgespeichert, wobei in einigen Verfahren erhebliche Datenmengen in der Größenordnung von vielen Gigabyte entstehen können. Zur Interpretation werden üblicherweise – so man sich nicht auf eine Kartendarstellung und qualitative Näherungsabschätzungen von Störkörpertiefe und -ausdehnung beschränkt – zwei- oder dreidimensionale Verfahren, wie die Finite-Element-Methode oder Finite-Differenzen-Verfahren, angewandt, die häufig einen großen Aufwand an Rechenzeit und Speicherbedarf erfordern. Einfache eindimensionale Modell- oder Inversionsrechnungen gehören dagegen heute zum Standard der Datenevaluation, die bereits im Gelände durchgeführt wird. Obwohl die elektromagnetischen Verfahren im Prinzip eindeutig sind, führen große Änderungen der Modellparameter oftmals nur zu geringen Änderungen der Modellantwort (sog. schlecht gestelltes Problem der Inversionsaufgabe). Zur Einschränkung der möglichen Modellvielfalt werden häufig verschiedene Verfahren gemeinsam angewendet. So kann z.B. der Einfluß eines static shift in der Magnetotellurik durch ergänzende Gleichstromgeoelektrik- oder TEM-Messungen (Transienten-Elektromagnetik) verkleinert werden. Sinnvoll ist auch eine Kombination elektromagnetischer mit seismischen Untersuchungen. Zwar bestehen keine eindeutigen Zusammenhänge zwischen elektrischer Leitfähigkeit und seimischen Geschwindigkeiten, doch sind immer wieder Zonen erhöhter Dämpfung seismischer Wellen und Reflektivität in der tiefen Kruste gefunden worden, die sich mit ausgeprägten Anomalien der Leitfähigkeit korrelieren lassen. Die aktuelle theoretische Forschung auf dem Gebiet der elektromagnetischen Verfahren beschäftigt sich insbesondere mit den Problemen anisotroper Leitfähigkeit und der dreidimensionalen Vorwärts- und Inversionsrechnung. Die geowissenschaftlichen Probleme umfassen insbesondere das elektromagnetische Abbild von Störungszonen und die Korrelation von Laborbefunden mit Oberflächenmessungen. Ein sehr großes Gewicht hat die Elektromagnetik bei der Lösung umweltrelevanter Fragestellungen erlangt; hierbei stellen die gemeinsame Interpretation der Ergebnisse unterschiedlicher Methoden und die Überprüfbarkeit durch Bohrungen die größten Herausforderungen dar. [HBr]
elektromagnetische Verfahren 1: Veranschaulichung von quasihomogenen und inhomogenen Quellenfeldern über einer elektrisch leitfähigen Erde. Im Luftraum ist die Wellenlänge λ0 sehr viel größer als im Untergrund (λ1 bzw. λ2). elektromagnetische Verfahren 1:

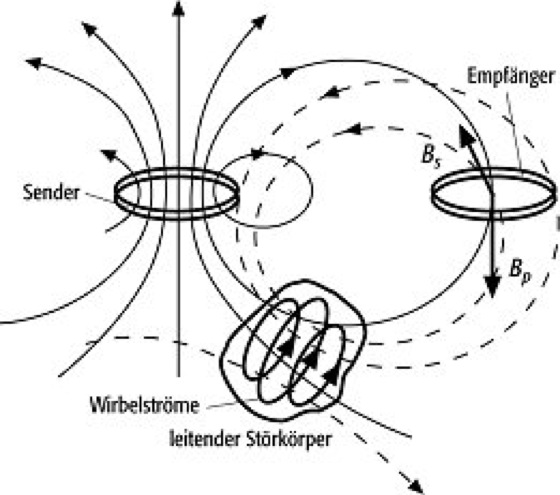
elektromagnetische Verfahren 2: Prinzip der elektromagnetischen Induktionsverfahren, hier dargestellt für ein Zweispulensystem. Bp ist das primäre, Bs das sekundäre Feld am Ort der Empfängerspule. elektromagnetische Verfahren 2:
elektromagnetische Verfahren 3: Kopplung eines Empfängers an einen Sender und den Untergrund, der durch eine Leiterschleife mit der Induktivität L2 und dem Ohmschen Widerstand R realisiert wird. elektromagnetische Verfahren 3:

elektromagnetische Verfahren 4: Slingram-Kartierung einer graphitisierten Störungszone bei Rittsteig im Böhmerwald. elektromagnetische Verfahren 4:

elektromagnetische Verfahren 5: gebräuchliche Anordnungen in der aktiven Elektromagnetik. Die Bezeichnungen vertikal/horizontal beziehen sich auf die Ausrichtung der Spulenachsen zur Erdoberfläche. elektromagnetische Verfahren 5:

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.