Lexikon der Geowissenschaften: Tensor
Tensor, Schema von Maßzahlen (Tensorkomponenten) zur Darstellung der Richtungsabhängigkeit physikalischer Größen und physikalischer Eigenschaften in anisotropen Materialien (Anisotropie).
Tensoren sind über ihre Transformationseigenschaften gegenüber Koordinatentransformation definiert. Die Transformation der Basis eines dreidimensionalen Vektorraums B=(b1,b2,b3) wird durch eine 3×3-Matrix P=(pjk) dargestellt: b'j=pjkbk. Dabei ist immer die Einsteinsche Summenkonvention angewandt: Über gleichlautende Indizes wird summiert. Da es sich bei der Basistransformation um eine starre Bewegung handeln soll, die Winkel und Abstände unverändert läßt, ist der Wert der Determinate von P eins: |P|=1. Die Komponenten eines Vektors transformieren sich jedoch kontragredient bezüglich der Transformation der Basis des Vektorraums (Achsen des Koordinatensystems), d.h. mit der zu P inversen Matrix Q=(qnm), Q=P-1, die so definiert ist, daß das Matrizenprodukt QP=I die 3×3-Einheitsmatrix I mit ijk=δjk (δ=Kronecker-Symbol) ergibt. Folglich transformieren sich dann die Komponenten eines polaren Vektors:
vn'=qnmvm.
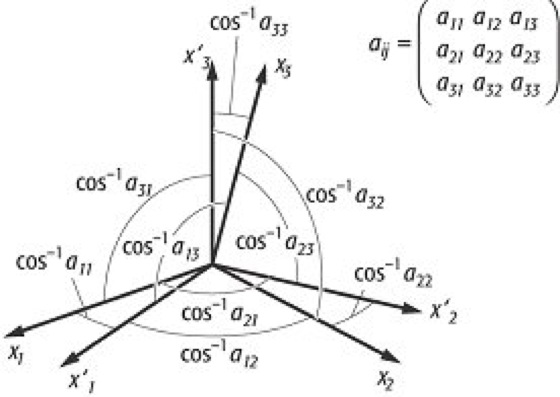
Für orthogonale (kartesischen) Koordinatensysteme ergibt sich die Transformationsmatrix ( Abb.) aus:
wobei das Koordinatensystem X'j in das Koordinatensystem Xj transformiert wird. Für orthogonale Transformationen erhält man Q einfach durch Transponieren von P, d.h. durch vertauschen der Zeilen und Spalten der Matrix P. Dann transformieren sich Basis und Vektoren in gleicher Weise.
Die Stufe (Ordnung) eines Tensors ergibt sich aus der Anzahl der benötigten Transformationsmatrizen, die für seine Transformation notwendig sind. Die zur Beschreibung der Richtungsabhängigkeit notwendigen Tensorkomponenten werden durch Indizes gekennzeichnet. Die Stufe s des Tensors bestimmt die Anzahl der Indizes. Jeder Index kann im dreidimensionalen Raum die Werte 1, 2, 3, bezogen auf die drei linear unabhängigen Achsen eines kartesischen Koordinatensystems, annehmen. Daraus ergibt sich die Anzahl der Tensorkomponenten eines Tensors s-ter Stufe zu 3s. Jeder Index transformiert sich wie die Komponente eines Vektors. Daraus folgt das Transformationsverhalten der Komponenten eines polaren Tensors s-ter Stufe:
Die Summe auf der rechten Seite läuft über alle Tensorkomponenten und besteht im allgemeinen aus 3s Summanden. Für eine bestimmte Komponente eines Tensors 2. Stufe t'j1j2 sieht diese Gleichung beispielsweise ausgeschrieben wie folgt aus:
dabei laufen die Summen über l und k unabhängig von einander von 1 bis 3, also über alle neun Komponenten tlk.
Polare und axiale Tensoren unterscheiden sich hinsichtlich ihres Transformationsverhaltens, wenn mit der Transformation P* eine Inversion P*=(-1)P verknüpft ist. Dann nimmt die Determinante von P* den Wert -1 an: |P*|=|Q*|=-1. Die Komponenten polarer Vektoren ändern ihr Vorzeichen unter einer solchen Transformation, da jede Vektorkomponente mit -1 multipliziert wird. Der die physikalische Größe beschreibende Vektor muß bei Wechsel des Koordinatensystems unverändert im Raum bleiben, d.h. im neuen, invertierten Koordinatensystem müssen daher die Komponenten das Vorzeichen wechseln. Axiale Tensoren treten immer dann auf, wenn magnetische Größen im Spiel sind, denn das magnetische Feld ist beispielsweise ein axialer Vektor, dessen Entstehung auf elementare Kreisströme zurückgeführt werden kann. Die Komponenten eines Kreisstroms behalten jedoch bei der Transformation mit einer Inversion ihre Vorzeichen bei, d.h. die Umlaufrichtung ist invariant gegenüber Inversion. Das Magnetfeld hätte vom neuen invertierten Koordinatensystem aus betrachtet seine Richtung im Raum umgekehrt. Denn die Richtung des Magnetfeldes und die Umlaufrichtung des Kreisstroms sind in einem rechtshändigen Koordinatensystem über die Rechtshandregel verknüpft. Bei Inversion kehrt sich die Händigkeit des Koordinatensystems um, d.h. die im Raum unveränderte Umlaufrichtung des Kreisstroms ergibt jetzt mit der Linkshandregel ein Magnetfeld mit umgekehrter Richtung. Diese Richtungsänderung wird durch Einbeziehen des Wertes der Determinante der Transformationsmatrix in die definierende Transformationsvorschrift für axiale Tensoren berücksichtigt:
Die Verknüpfung polarer p- und axialer a-Tensoren ist durch folgende Regeln definiert: p=pp, p=aa, a=ap, a=pa.
Die Anzahl der von Null verschiedenen und unabhängigen Komponenten wird durch die Symmetrie des Materials festgelegt. Aus dem Symmetrieprinzip: In symmetrisch äquivalenten Richtungen muß das physikalische Verhalten dasselbe sein, folgen den sog. Reduktionsbeziehungen für die Tensorkomponenten. Sie müssen invariant gegenüber solchen Koordinatentransformationen sein, die Symmetrieoperationen entsprechen; d.h. formal: Die transformierten Tensorkomponenten sind gleich den entsprechenden (d.h. mit der gleichen Abfolge der Indizes) ursprünglichen Komponenten:
Die Symmetrieoperation Drehung um 90º um die c-Achse z.B. wird durch die Transformationsmatrix:
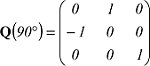
dargestellt. Daraus ergeben sich die folgende Reduktionsbeziehungen für einen Tensor 2. Stufe: t11=t22; t33=t33; t12=-t21=-t12. Wegen der vielen Nullen in der Transformationsmatrix reduziert sich die Transformationsvorschrift auf einen Summanden. Die letzte Bedingung kann nur erfüllt werden mit t12=t21=0. Ferner ist t13=t23=-t13 und t23=-t13=-t23. Auch diese Bedingungen können nur erfüllt werden, wenn die Komponenten verschwinden. Dann hat ein Tensor 2. Stufe in allen Kristallklassen des tetragonalen Kristallsystems, da sie alle die Drehachse 4 mit den Symmetrieoperationen Drehung um Vielfache von 90º enthalten, folgendes Aussehen:
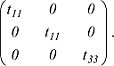
In der Tabelle 1 ist das Komponentenschema der symmetrischen polaren Tensoren 2. Stufe für die Kristallsysteme zusammengestellt.
Tensoren nullter Stufe mit einer Komponente heißen Skalare; sie beschreiben richtungsunabhängige physikalische Eigenschaften, wie z.B. spezifische Wärme und spezifische Dichte. Tensoren 1. Stufe mit drei Komponenten nennt man auch Vektoren. Ein physikalisches Beispiel ist die Pyroelektrizität. Durch Tensoren 2. Stufe werden u.a. folgende Eigenschaften beschrieben: optische Eigenschaften, elektrische Leitfähigkeit, Wärmeleitfähigkeit. Die Richtungsabhängigkeit der piezoelektrischen Eigenschaften wird durch einen polaren Tensor 3. Stufe beschrieben. Die Darstellung des Zustandes eines anisotropen Materials unter mechanischer Spannung oder Dehnung erfordert jeweils einen Tensor 2. Stufe. Damit lassen sich die elastischen Eigenschaften im Bereich der Gültigkeit des Hookschen Gesetzes durch einen Tensor 4. Stufe beschreiben (Tab. 2).
Tensor (Tab. 1): Komponentenschema eines symmetrischen, polaren Tensors 2. Stufe für die verschiedenen Kristallsysteme (n=Zahl der unabhängigen Komponenten). Tensor (Tab. 1):
![](javascript:ShowPic("/lexika/images/geo/f5f2164.jpg", "276", "296");)
Tensor (Tab. 2): Transformationsregeln für Tensoren 0. bis 4. Stufe. Tensor (Tab. 2):
![](javascript:ShowPic("/lexika/images/geo/f5f2163.jpg", "276", "196");)
Tensor: Transformationsmatrix. Tensor:
![](javascript:ShowPic("/lexika/images/geo/f5f2165.jpg", "457", "222");)
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.