Zuordnung f zwischen zwei Mengen A und B, die jedem Element der Menge A genau ein Element der Menge B zuordnet.

Mengentheoretisch ist eine Abbildung eine links-totale rechtseindeutige Relation zwischen zwei Mengen A und B, d. h. ein geordnetes Tripel (A, B, f). Die Menge f ist eine Teilmenge von A × B mit der Eigenschaft, daß für jedes Element x ∈ A genau ein Element y ∈ B existiert mit (x, y) ∈ f. Oftmals ist es klar, um welche Mengen A und B es sich handelt, und die Menge f wird mit der Abbildung (A, B, f) identifiziert.

Die Menge A heißt Definitions- oder Urbildbereich, bezeichnet mit D(f) oder D_f, und B heißt Werte- oder Bildbereich, bezeichnet mit R(f) oder R_f. Man schreibt auch \begin{eqnarray}\begin{array}{cc}f:A\to B, & x\mapsto y\end{array}\end{eqnarray}

und nennt x ↦ y Abbildungsvorschrift von f. Ist (x, y) ∈ f, so wird y auch als f(x) bezeichnet. Ist T ⊆ A, so heißt die Menge \begin{eqnarray}f(T):=\{f(x)\in B:x\in T\}\end{eqnarray}

das Bild von T unter der Abbildung f, f(A) heißt das Bild von f. Ist hingegen U eine Teilmenge von B, so heißt die Menge \begin{eqnarray}{f}^{-1}(U):=\{x\in A:f(x)\in U\}\end{eqnarray}

das Urbild von U unter f. Der Graph der Abbildung f ist die Menge {(x, f(x)) ∈ A × B : x ∈ A}. Geometrische Veranschaulichungen dieser Menge werden ebenfalls als Graph von f bezeichnet.

Beispiel: Man betrachte die Abbildung f : [−2, 2] → ℝ, x ↦ x². Der Definitionsbereich besteht aus dem abgeschlossenen Intervall [−2, 2], der Bildbereich sind die reellen Zahlen. Das Bild von f ist das abgeschlossene Intervall [0, 4]. Für T := [−1, 0] gilt f(T) = [0, 1]. Für U := [−1, 0.25] gilt f⁻¹(U) = [−0.5, 0.5]. Die Abbildung zeigt den Graph der Abbildung f, wobei, wie üblich, die horizontale Achse den Definitions-bereich und die vertikale Achse den Wertebereich darstellt.

Beispiel: Man betrachte die Abbildungen f : [−1, 1] → ℝ, x ↦ x² und g : [−1, 1] → ℝ, \(x\mapsto \frac{1}{4}x\). Dann gilt \begin{eqnarray}f([-1,1])=[0,1]\subseteq D(g)\end{eqnarray}

und \begin{eqnarray}g([-1,1])=[-\frac{1}{4},\frac{1}{4}]\subseteq D(f).\end{eqnarray}

Es ergeben sich die Kompositionen \(g\circ f:[-1,1]\mapsto {\mathbb{R}},(g\circ f)(x)=g(f(x))=g({x}^{2})=\frac{1}{4}{x}^{2}\) und \(f\circ g:[-1,1]\mapsto {\mathbb{R}},(f\mathrm{\circ }g)(x)=f(g(x))=f(\frac{1}{4}x)=\frac{1}{16}{x}^{2}\). Das Beispiel zeigt, daß die Komposition von Abbildungen i.allg. selbst dann nicht kommutativ ist, wenn Definitions- und Wertebereich der komponierten Abbildungen übereinstimmen.

Das Komponieren von Abbildungen ist hingegen assoziativ, das heißt, für drei Abbildungen f :A→B, g : C → D, h : E → F mit f(A) ⊆ C und g(C) ⊆ E gilt \begin{eqnarray}(h\circ g)\circ f=h\circ (g\circ f).\end{eqnarray}

Es seien f : A → B und g : B → C Abbildungen, I eine Indexmenge, die Mengen S, T, S_i, i ∈ I seien Teilmengen von A, die Mengen U, V, U_i, i ∈ I seien Teilmengen von B, und W sei eine Teilmenge von C. Dann gelten die folgenden Gesetze bezüglich Abbildungen und verschiedenen Verknüpfungsoperationen von Mengen: \begin{eqnarray}\begin{array}{lll}f(S\cap T) & \subseteq & f(S)\cap f(T),\\ f(\displaystyle \mathop{\cap }\limits_{i\in I}{S}_{i}) & \subseteq & \displaystyle \mathop{\cap }\limits_{i\in I}f({S}_{i}),\\ f(S\cup T) & = & f(S)\cup f(T),\\ f(\displaystyle \mathop{\cup }\limits_{i\in I}{S}_{i}) & = & \displaystyle \mathop{\cup }\limits_{i\in I}f({S}_{i}),\\ {f}^{-1}(U\cap V) & = & {f}^{-1}(U)\cap {f}^{-1}(V),\\ {f}^{-1}(\displaystyle \mathop{\cap }\limits_{i\in I}{U}_{i}) & = & \displaystyle \mathop{\cap }\limits_{i\in I}{f}^{-1}({U}_{i}),\\ {f}^{-1}(U\cup V) & = & {f}^{-1}(U)\cup {f}^{-1}(V),\\ {f}^{-1}(\displaystyle \mathop{\cup }\limits_{i\in I}{U}_{i}) & = & \displaystyle \mathop{\cup }\limits_{i\in I}{f}^{-1}({U}_{i}),\\ f({f}^{-1}(U)) & \subseteq & U,{f}^{-1}(f(S))\supseteq S,\\ {f}^{-1}(U\backslash V) & = & {f}^{-1}(U)\backslash {f}^{-1}(V),\\ {(g\circ f)}^{-1}(W) & = & {f}^{-1}({g}^{-1}(W)).\end{array}\end{eqnarray}

Das folgende Beispiel zeigt, daß sich i.allg. die Teilmengenbeziehungen nicht durch eine Gleichheit ersetzen lassen. Für die Abbildung f : {1, 2} → { 1, 2}, f(1) = f(2) = 1, ist f({1} ∩ {2}) = ø ⊊ {1} = f({1}) ∩ f({2}), f(f⁻¹({1, 2})) = {1} ⊊ {1, 2}, f⁻¹(f({1})) = {1, 2} ⊋ {1}.

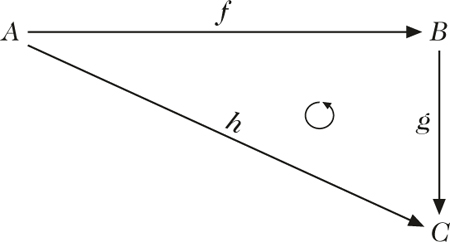
Oft veranschaulicht man sich den Zusammen-hang zwischen Abbildungen in einem Abbildungsdiagramm. Im einfachsten Fall wird eine Abbildung f : A → B dargestellt: \begin{eqnarray}A\mathop{\to }\limits^{f}B.\end{eqnarray}

Sind Abbildungen f : A → B, g : B → C, h : A → C, gegeben, so lassen sie sich als folgendes Diagramm darstellen:

Abbildungen mit speziellen Eigenschaften (man vergleiche hierzu auch die jeweiligen speziellen Stichwortartikel):

Eine Abbildung f : A → B heißt surjektiv genau dann, wenn f(A) = B, das heißt, wenn der Wertebereich von f mit dem Bild von f übereinstimmt. Man spricht dann auch von einer Abbildung auf die Menge B und schreibt f : A ↠ B. Die surjektiven Abbildungen sind genau die bitotalen rechtseindeutigen Relationen. f heißt injektiv (oder auch eineindeutig, Injektion, Einbettungsabbildung, Einbettung, Inklusionsabbildung, Inklusion) genau dann, wenn für alle y ∈ B gilt, daß #f⁻¹({y}) ∈ {0, 1}, das heißt, jedes Element des Bildbereiches von f ist das Bild höchstens eines Elementes des Urbildbereiches von f. Man schreibt dann auch f : A ↪ B. Die injektiven Abbildungen sind genau die links-totalen eineindeutigen Relationen.

Die Abbildung f heißt bijektiv genau dann, wenn sie sowohl surjektiv als auch injektiv ist. Die bijektiven Abbildungen sind genau die bitotalen eineindeutigen Relationen. Ist A eine Teilmenge von B, so heißt die Abbildung i : A → B, x ↦ x Inklusionsabbildung (oder auch Einbettungsabbildung, Inklusion, Einbettung) von A in B. Gilt sogar A = B, so schreibt man I_A := Id_A := i und nennt I_A die Identität (auch identische Abbildung, Eins-Abbildung) auf A. Eine Abbildung f : A → B (A ⊆ B nicht länger vorausgesetzt) ist genau dann surjektiv, wenn es eine Abbildung g : B → A gibt, so daß f ∘ g = I_B; f ist genau dann injektiv, wenn es eine Abbildung g : B → A gibt, so daß g ∘ f = I_A. Ist f sogar bijektiv, so stimmen die durch Surjektivität und Injektivität gegebenen Abbildungen überein. Die so erhaltene Abbildung wird mit f⁻¹ : B → A bezeichnet und die Umkehrabbildung (bzw. Umkehrfunktion, inverse Abbildung) von f genannt.

Beispiele:

Die Abbildung s : {1, 2} → {4, 5, 6}, x ↦ x + 3 ist injektiv, jedoch nicht surjektiv. Für die Abbildung s_l : {4, 5, 6} → {1, 2}, s_l(4) = 1, s_l(5) = s_l(6) = 2 gilt s_l ∘ s = I_{1,2}. Jedoch gibt es keine Abbildung s_r : {4, 5, 6} → {1, 2} mit s ∘ s_r = I_{4,5,6}. Umgekehrt ist die Abbildung s_l surjektiv, jedoch nicht injektiv. Es gibt somit keine Abbildung s_ll : {1, 2} → {4, 5, 6} mit s_ll ∘ s_l = I_{4,5,6}.

Die Abbildung f : {1, 2, 3} → {4, 5, 6}, x ↦ x + 3 ist bijektiv und hat die Umkehrabbildung f⁻¹ : {4, 5, 6} → {1, 2, 3}, x ↦ x − 3.

Eine Abbildung mit der leeren Menge als Definitionsbereich heißt leere Abbildung. Der Graph einer solchen Abbildung ist ebenfalls die leere Menge. Eine Abbildung f : A → B heißt genau dann konstant, wenn das Bild von f aus genau einem Element des Wertebereichs besteht. Beispiel: \(f:{{\mathbb{R}}}_{0}^{+}\to {\mathbb{R}},x\mapsto -1\).

f : A → B heißt multivariate Abbildung, Abbildung von n Variablen, oder n-stellig, n ∈ ℕ, genau dann, wenn A Teilmenge des kartesischen Produktes M₁ × ⋯ × M_n der n Mengen M₁, … M_n ist. Man schreibt dann oft f(x₁, …, x_n) anstatt f((x₁, …, x_n)).

Ein Beispiel für eine n-stellige Abbildung ist die euklidische Norm \(N:{{\mathbb{R}}}^{n}\to {{\mathbb{R}}}_{0}^{+}\), \begin{eqnarray}N({x}_{1},\ldots ,{x}_{n})=\sqrt{{x}_{1}^{2}+\cdots +{x}_{n}^{2}}.\end{eqnarray}

Ist G eine Gruppe, so ist p : ℤ × G → G, (k, g) ↦ g^k ein Beispiel für eine zweistellige Abbildung. Ist F der Graph einer Abbildung f : A → B, so sind die Projektionen \begin{eqnarray}{\pi }_{1}:F\to A,{\pi }_{1}(x,f(x))=x\end{eqnarray}

und \begin{eqnarray}{\pi }_{2}:F\to B,{\pi }_{2}(x,f(x))=f(x)\end{eqnarray}

weitere Beispiele für zweistellige Abbildungen.

Die Abbildung g : C → B heißt Einschränkung der Abbildung f : A →B genau dann, wenn C eine Teilmenge von A ist und g(x) = f(x) für alle x ∈ C gilt. Man schreibt g = f|C (lies: f eingeschränkt auf C). Umgekehrt wird dann f als Fortsetzung der Abbildung g bezeichnet.

Beispiel: Die konstante Funktion h : ℝ⁺ → {−1, 0, 1}, x ↦ 1 ist eine Einschränkung der Signumfunktion sign : ℝ → {−1, 0, 1}.

Eine Abbildung f, deren Definitionsbereich aus den natürlichen Zahlen besteht, heißt Folge. Übliche Bezeichnungen sind f = (a_n)_n∈ℕ0 = (a₀, a₁, a₂, …). Auch Abbildungen, deren Definitionsbereich zwar abzählbar und linear geordnet, jedoch von den natürlichen Zahlen verschieden ist, werden gelegentlich als Folge bezeichnet. Ist der Definitionsbereich eine endliche Menge, so wird die Abbildung manchmal als endliche Folge bezeichnet.

Beispiele für Folgen sind

(3(n + 1) + 1)_n∈ℕ0 = (4, 7, 10, …),

\({({(\frac{1}{2})}^{n})}_{n\in {{\mathbb{N}}}_{0}}=(1,\frac{1}{2},\frac{1}{4},\ldots ),\)

(p^p)_{p∈{p: p ist Primzahl}} = (4, 27, 3125, …),

(2k)_k∈ℤ = (…, −2, 0, 2, …),

\((-1,-\frac{1}{2},0,\frac{1}{2},1)\).

Soll hervorgehoben werden, daß es sich beim Wertebereich der Abbildung ℱ : I → ℳ um eine Menge von Mengen handelt, so wird die Menge I häufig Indexmenge genannt und ℱ als eine Familie von Mengen bezeichnet. Man schreibt ℱ dann auch in der Form ℱ = (M_i)_i∈I, wobei M_i := ℱ(i) gesetzt wird.

Beispiel einer Familie von Mengen ist ({k ∈ ℤ : |k| ≤ n})_n∈ℕ.