Lexikon der Mathematik: Analysis
D. Hoffmann
Die Analysis (engl.: analysis, calculus; franz.: analyse) ist ein zentrales und außerordentlich anwendungsrelevantes Gebiet der Mathematik, das in engerem Sinne die Infinitesimalrechnung, d. h. Differential- und Integralrechnung, umfaßt und dazu all die Zweige der Mathematik, die wesentlich auf der Infinitesimalrechnung basieren, so etwa Differentialgleichungen (gewöhnliche und partielle), Integralgleichungen, Differenzengleichungen, Variationsrechnung, Spezielle Funktionen der mathematischen Physik, Vektoranalysis, Maß- und Integrationstheorie und Funktionalanalysis.
In weiterem Sinne können auch die Gebiete Approximationstheorie, Optimierungstheorie, Harmonische Analyse, Differentialgeometrie, Theorie der Minimalflächen und heute noch Globale Analysis, Analytische Zahlentheorie, Verallgemeinerte Funktionen (Distributionen und Hyperfunktionen) und Theorie der Pseudodifferentialoperatoren dazu gezählt werden, die sich aber alle mit eigenständigen Methoden und Fragestellungen unabhängig entwickelt haben.
Anwendungen findet die Analysis in der Wahrscheinlichkeitstheorie, sowie besonders in den Naturwissenschaften (vor allem der Physik), der Technik und Informatik (Ingenieurwissenschaften) und heute auch zunehmend in Wirtschafts-, Sozialund Finanzwissenschaften.
Im Schulbereich wird „Analysis“ auch enger als Synonym für Infinitesimalrechnung benutzt. Oft findet man die Abgrenzung zwischen klassischer Analysis und Funktionalanalysis, was aber heute nur noch schwer klar zu trennen ist; die Übergänge sind fließend.
Für das Universalgenie John von Neumann (1903–1957) war die Infinitesimalrechnung die herausragende Leistung der modernen Mathematik, ihre Bedeutung könne nur schwerlich überschätzt werden. Seiner Ansicht nach markiert sie unmißverständlicher als alles andere den Beginn der modernen Mathematik, und das System der mathematischen Analysis, welches ihre logische Weiterentwicklung ist, stelle den größten operativen Fortschritt im exakten Denken dar.
Grundlegende Begriffe und Aufgaben
Grundlegende Begriffe der Analysis sind – aufbauend auf den Begriffen Zahl und Funktion, speziell Folgen, dann Reihen und Potenzreihen – Stetigkeit und Grenzwert und damit Ableitung und Integral.
Der Grenzwertbegriff (Limes) präzisiert die intuitive vage Vorstellung, daß sich Funktionswerte einer Funktion f einem Wert s (beliebig) nähern, wenn sich die Argumente einem Punkt a nähern. Stetigkeit erfaßt mathematisch exakt die grobe Idee, daß sich die Funktionswerte nur wenig ändern, wenn sich die Argumente wenig verändern. Dieses ist keineswegs eine „akademische“ Fragestellung; denn in vielen Bereichen – auch des täglichen Lebens – möchte man sicher sein, daß sich kleine Veränderungen in irgendwelchen Eingabegrößen wenig – also gerade nicht „chaotisch“– auf das Ergebnis auswirken.
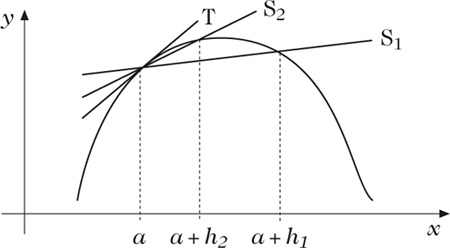
Die Grundaufgabe der Differentialrechnung ist die Berechnung der Ableitung f′(a) zu einer gegebenen Funktion f an einer Stelle a. Geometrisch gesprochen die Bestimmung der Steigung der Tangente an die durch f beschriebene Kurve im Punkt (a, f(a)).
Stetigkeit von f an der Stelle x0
Tangente als „Grenzlage“ der Sekanten
Beschreibt f die Länge eines Weges, den ein Massenpunkt bis zur Zeit t zurücklegt, dann ist f′(a) die Geschwindigkeit zur Zeit a. Bereits in den Arbeiten von Galileo Galilei (1564–1642) über den freien Fall steht implizit, daß (im dortigen Zusammenhang) Geschwindigkeit gleich Ableitung ist.
Die Grundaufgabe der Integralrechnung ist Flächenberechnung. Für Newton war dies das entscheidende Werkzeug, um aufbauend auf Keplers Planetengesetzen das Gravitationsgesetz und die Gleichungen der Mechanik per Abstraktion zu erhalten.
Der Fundamentalsatz der Analysis oder Hauptsatz der Differential- und Integralrechnung ist das entscheidende Bindeglied zwischen Integration und Differentiation und damit zentrales Hilfsmittel für die praktische Berechnung von Integralen. Erst dieses Zusammenspiel zwischen Differentiation und Integration macht die besondere Stärke der Analysis aus.
Flächenfunktion
Die Urprünge von Differentiation und Integration sind durchaus empirisch und irdisch: Keplers Integrationsversuch zur Volumenbestimmung von Weinfässern! Newtons „Fluxionsmethode“ ging von physikalischen Fragestellungen aus und wurde hauptsächlich für Zwecke der Mechanik entwickelt. Leibniz stellte das Tangentenproblem an den Anfang seiner Überlegungen. Für René Descartes (1596–1650) war es das „nützlichste und allgemeinste Problem“, das er kannte. Wesentliche Wurzeln für die Entstehung der Integralrechnung waren Probleme der allgemeinen Inhaltsmessung, insbesondere auch krummlinig begrenzter Bereiche. So dienen Integrale im einfachsten Fall zur Bestimmung von Längen, Flächen und Volumina. Dahinter verbergen sich in den verschiedenen Anwendungen Aufgaben wie zum Beispiel Berechnung von Arbeit, Weglängen, Potential, Kosten, Erlös und Gewinn.
Die Berechnung von Integralen über die Definition (etwa als Riemann-Integral) ist meist beschwerlich und viel zu aufwendig. Der Fundamentalsatz der Analysis zeigt, daß Stammfunktionen (Funktionen, die eine gegebene Funktion als Ableitung haben) ein sehr leistungsfähiges Hilfsmittel liefern, und dieses Vorgehen für stetige Integranden – prinzipiell – immer möglich ist. Die Bedeutung dieses – von Newton schon erahnten – Satzes für die Mathematik und ihre Anwendungen kann kaum überschätzt werden; er verbindet die beiden zentralen – ursprünglich und von der Fragestellung her völlig getrennten – Gebiete der Analysis Differential- und Integralrechnung. Eine wesentliche Aufgabe ist daher das kalkülmäßige Aufsuchen von Stammfunktionen für große Klassen von wichtigen Funktionen.
Pionierzeit – Bemühen um wissenschaftliche Strenge
Nach ersten Ansätzen in der Antike – etwa Zenon von Elea (ca. 495–435 v. Chr.; Achill und die Schildkröte), Eudoxos von Knidos (408–355 v. Chr.; Proportionenlehre und Exhaustionsmethode) und Archimedes von Syrakus (287–212 v. Chr.; Kompressionsverfahren und Exhaustionsmethode zur Flächen- und Volumenberechnung spezieller Flächen bzw. Körper) –, dann Wegbereitung und Lösung spezieller Fragestellungen durch Johannes Kepler (1571–1630), Bonaventura Cavalieri (1598–1647) und Pierre de Fermat (1601–1665) und vor allem nach der stürmischen Entwicklung der Mathematik im 17. und 18. Jahrhundert, begann ab etwa 1830 eine kritische Besinnung auf die Grundlagen, ein Bemühen um Strenge der mathematischen Deduktion; denn neben großartigen Erfolgen gab es in dieser Pionierzeit erhebliche Unklarheiten in Grundbegriffen und Beweismethodik und damit dann Widersprüche. Die damaligen Grundlagen stellten sich als inadäquat heraus, der Boden war schwankend. So in der Infinitesimalrechnung seit ihrer Begründung durch Gottfried Wilhelm von Leibniz (1646–1716) und Isaac Newton (1643–1727) etwa die nicht präzisierte Vorstellung von „unendlich kleinen Größen“. (Diese wurden erst 1961 in der Nichtstandard-Analysis von Abraham Robinson (1918–1974) zu wohldefinierten mathematischen Objekten.) Auch die durch Joseph Fourier (1768–1830) – ausgehend von Problemen der Wärmeleitung – begründete Theorie der nach ihm benannten Reihen erforderte eine Präzisierung der grundlegenden Begriffe.
Entscheidende Klärungen wurden durch Augustin Louis Cauchy (1789–1857), Johann Carl Friedrich Gauß (1777–1855) und Bernhard Bolzano (1781–1848) erreicht, fortgesetzt und ausgefeilt durch Karl Weierstraß (1815–1897) – bei der Einführung in die Analysis ist die „Weierstraßsche Strenge“ sprichwörtlich –, Georg Cantor (1845– 1918) und Richard Dedekind (1831–1916). Dadurch wurde die Entwicklung neu belebt und vehement vorangetrieben. Die von Cantor eingeführte Mengenlehre veränderte die Analysis grundlegend. Darauf bauten die Beiträge auf von René-Louis Baire (1874–1932), Émile Borel (1871–1956) und Henri Lebesgue (1875–1941), dessen Integral – das Lebesgue-Integral – heute den Integralbegriff für das analytische Arbeiten und viele Anwendungen darstellt.
Reelle Analysis – Komplexe Analysis
Die Theorie der Funktionen reeller Variabler wird abgrenzend auch als reelle Analysis bezeichnet, die der Funktionen komplexer Variabler, auf die an anderer Stelle eingegangen wird, als komplexe Analysis, speziell Funktionentheorie. Die Funktionentheorie hat sich von der reellen Analysis mit eigenständigen Methoden und andersartigen Themen abgesetzt; viele Phänomene im Reellen werden aber erst verständlich, wenn man den Übergang zum Komplexen macht. Die frühzeitige Einbeziehung komplexer Zahlen bringt aber auch in rein reellen Fragestellungen vielfach erstaunliche Vereinfachungen, so daß dies heute weitgehend Standard in der (Hochschul-) Lehre ist.
Eindimensionale reelle Analysis
Stichwortartig sei grob ein Aufbau der eindimensionalen reellen Analysis skizziert, wie er heute zumindest im Kern Standard in vielen Analysis-Vorlesungen ist:
Axiomatische Einführung der reellen Zahlen (ℝ), damit der natürlichen (ℕ), ganzen (ℤ), rationalen (ℚ) und dann der komplexen Zahlen (ℂ); Zusammenspiel von algebraischen (Körper) und topologischen Gesichtspunkten (hier über Ordnungsstruktur); Folgerungen aus dem Vollständigkeitsaxiom; Folgen, Reihen, Potenzreihen (Konvergenzbegriff); Stetigkeit (u. a. Zwischenwertsatz und Satz über die Annahme von Extremwerten), gleichmäßige Stetigkeit; Differentialrechnung: U.a. Satz von Rolle und Mittelwertsatz mit Folgerungen für lokales Verhalten und damit Extremwertbestimmung gewisser Funktionen; Differentiation von Potenzreihen und der Umkehrfunktion; Höhere Ableitungen mit Folgerungen über Krümmung (Konvexität, Konkavität); Stammfunktionen (unbestimmte Integrale); Bestimmtes Integral, Flächeninhalt; Funktionenfolgen, gleichmäßige Konvergenz; Taylor-Reihen; Uneigentliche Integrale.
Mehrdimensionaler Fall
Bei der Verallgemeinerung auf den mehrdimensionalen Fall ist die Betrachtung von Funktionen f : D → ℝn mit D ⊂ ℝ (und einer natürlichen Zahl n) durch Zurückführung auf Koordinatenfunktionen recht einfach. Aber schon die Betrachtung von Funktionen f : ℝ2 → ℝ ist etwas schwieriger. Dabei sind geometrische Vorstellung („Fläche“ im ℝ3) und dazu graphische Darstellungen wie etwa durch Niveauoder Höhenlinien und Vertikalschnitte hilfreich:
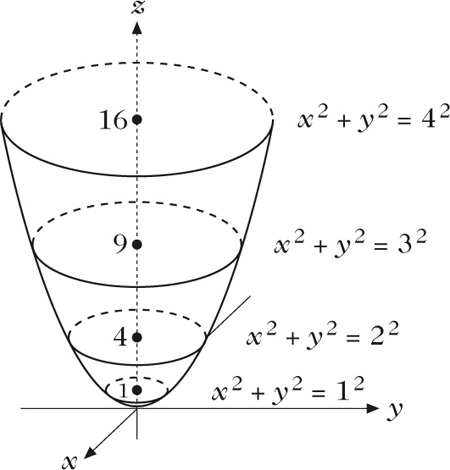
Bei der durch f(x, y) := x2 +y2 definierten Funktion f : ℝ2 → ℝ sind die nicht-trivialen Höhenlinien Kreise. Dreidimensional gezeichnet, sieht das ungefähr so aus:
Höhenlinien
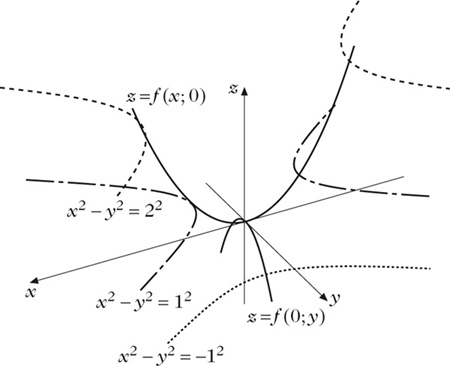
Für f : ℝ2 → ℝ, definiert durch f(x, y) := x2 −y2, sind die Niveaulinien Hyperbeln. Ergänzt man dies durch die beiden „Vertikalschnitte“ f(0, y) = −y2 und f(x, 0) = x2, so gewinnt man schon einen guten Überblick über den Graphen. Die anschließende dreidimensionale Zeichnung vermittelt mit den Höhenlinien und den angegebenen Vertikalschnitten einen ungefähren Eindruck.
Höhenlinien und Vertikalschnitte
Heute erhält man mit leistungsfähigen Computeralgebrasystemen, zum Beispiel Mathematica oder Maple, ganz einfach ansprechende Graphiken – mit zahlreichen Optionen für die Darstellung (Farben, Drehen, Stauchen, Schattierung, …).
Ein beliebtes Beispiel ist etwa der Affensattel.
Eine Einführung in die mehrdimensionale Analysis wird zumindest enthalten: Topologische Grundbegriffe für die Analysis im ℝn: Der ℝn als normierter Vektorraum, Konvergenz, Kompaktheit; Stetigkeit und Grenzwert; Zusammenhang; Differenzierbare Abbildungen: Totale und partielle Differenzierbarkeit; Mittelwertsatz; Fehlerabschätzungen; Höhere (partielle) Ableitungen, Satz von Schwarz; Satz von Taylor; Lokale Extremwerte; Lokale Umkehrbarkeit; Implizite Funktionen; Extrema mit Nebenbedingungen (Lagrange-Multiplikatoren); Umkehrung der Differentiation: Kurven und Kurvenintegrale; Hauptsätze (zum Umkehrproblem); Integral auf dem ℝn: Inhalt und Meßbarkeit; Iterierte Integration; Transformationssatz (Substitutionsregel); Integralsätze von Gauß und Stokes.
Absolute Analysis
Die moderne Analysis verdankt ihren Erfolg – neben ein- bzw. mehrdimensionaler reeller Analysis – wesentlich dem Einsatz von Techniken der Funktionalanalysis, der Maßtheorie und der Topologie.
Die Funktionalanalysis ist die wichtige Verallgemeinerung der klassischen Analysis, dabei heute kaum noch von ihr klar abzugrenzen. In der Entwicklung der Funktionalanalysis, angeregt durch die bahnbrechenden Überlegungen von David Hilbert (1862–1943), Erhard Schmidt (1876–1959) und Frigyes Riesz (1880–1956), brachte John von Neumann 1928 die entscheidende Idee: Die Theorie wurde von den Schranken Koordinatendarstellung und Matrizenkalkül befreit und zu einer koordinaten- und dimensionsfreien Theorie gestaltet. Eine moderne Analysis sollte sich heute daran orientieren! Die Elimination der Koordinaten bringt nicht nur formalen Gewinn. Sie führt zu Durchsichtigkeit und Einfachheit auch in der Theorie der Funktionen mehrerer Variabler. Allgemeiner als die bis dahin betrachteten Hilberträume führte 1920 Stefan Banach (1892–1945) die später nach ihm benannten Banachräume ein, die heute Standard für viele Theorien sind. Die Strukturen werden übersichtlich und deutlich, was Erlernen und Weiterentwicklung der Ideen entscheidend fördert. Ein solcher moderner Kalkül hat auch wesentliche Vorteile in den Anwendungen, so etwa in der theoretischen Physik.
Zudem ist die Beschäftigung damit (Spektraltheorie in abstrakten Hilbert-Räumen) ohnehin zwingend, wenn man die Quantentheorie mathematisch befriedigend behandeln will. Die Erweiterung ist naheliegend und eigentlich zwingend; sie drängt sich auch aus Fragestellungen der klassischen Analysis heraus auf, zum Beispiel: In der Variationsrechnung sind die unabhängigen Größen nicht Zahlen oder Vektoren im ℝn, sondern Funktionen. So untersuchte z. B. schon Leonhard Euler (1707–1783) das Problem, eine Funktion y zu finden, die ein Funktional \begin{eqnarray}\displaystyle \underset{a}{\overset{b}{\int }}F(x,y(x),{y}^{\prime}(x))dx\end{eqnarray}
extremal macht, wobei alle stückweise stetig differenzierbaren Funktionen y : [a, b] → ℝ mit y(a) = A, y(b) = B – bei vorgegebenen reellen Zahlen a, b, A, B mit a < b – zugelassen sind. Die resultierende Euler-Lagrange-Gleichung wurde wesentlich zunächst für die Mechanik und später auch für die Quantenmechanik.
Beziehung zu den Anwendungen
Die Analysis bezieht, wie vorne schon gesagt, viele ihrer Fragestellungen und wichtige Impulse aus den Naturwissenschaften (vor allem der Physik), der Technik und Informatik (Ingenieurwissenschaften) und heute auch aus Wirtschafts-, Sozialund Finanzwissenschaften. Dabei resultiert aus der Allgemeinheit und Abstraktheit der grundlegenden Begriffe und Methoden ihre universelle Anwendbarkeit in den sehr unterschiedlichen Anwendungsbereichen. Ganz wichtig ist dabei, jeweils die „richtige“ Übersetzung in die Sprache der Mathematik zu finden (Modellierung). Explizite Lösungsformeln sind bei vielen Fragestellungen, die Anwender an die Mathematik stellen, eher der Ausnahmefall. Deshalb sind abstrakte Existenz- und Eindeutigkeitssätze auch für Anwender durchaus wichtig.
Die Analysis erhält aus den genannten Fächern durch schwierige Aufgaben immer wieder entscheidende Impulse. Die Bedeutung der wechselseitigen Beziehungen zwischen der Analysis und den Naturwissenschaften und allgemeiner Wissenschaften, die die Erfahrung auf einer höheren Ebene als der rein beschreibenden interpretieren, kann kaum überschätzt werden. Die Theorie steht in andauerndem fruchtbaren Kontakt zu diesen Wissenschaften, wobei diese einerseits wertvolle Hilfe durch die Theorie erfahren, andererseits diese immer wieder mit konkreten Problemen neu beleben und fordern.
Dadurch ist die Analysis weniger als manche andere Bereiche in der Mathematik ausschließlich der Eigendynamik gefolgt, weniger in Gefahr, durch „mathematische Inzucht“ in Richtung „l’art pour l’art“ zu degenerieren.
Literatur
[1] Amann, H.: Analysis 1, 2. Birkhäuser Basel, 1998, 1999.
[2] Blatter, C.: Analysis I, II, III. Springer-Verlag Berlin, 1991, 1992, 1981.
[3] Bourbaki, N.: Fonctions d’une variable réelle. Hermann Paris, 1976.
[4] Cartan, H.: Differentialformen. B.I.-Wissenschaftsverlag Mannheim, 1974.
[5] Dedekind, R.: Was sind und was sollen die Zahlen., 1888.
[6] Dieudonné: Grundzüge der modernen Analysis 1–9. Vieweg-Verlag Braunschweig, 1975–1987.
[7] Heuser, H.: Lehrbuch der Analysis, Teil 1, 2. Teubner-Verlag Stuttgart, 1993.
[8] Hoffmann, D.: Analysis für Wirtschaftswissenschaftler und Ingenieure. Springer-Verlag Berlin, 1995.
[9] Kaballo, W.: Einführung in die Analysis I, II, III. Spektrum Akademischer Verlag Heidelberg, 1996, 1997, 1999.
[10] Lang, S.: Undergraduate Analysis. Springer-Verlag New York, 1983.
[11] Rudin, W.: Analysis. Oldenbourg Verlag, 1998.
[12] Walter, W.: Analysis 1, 2. Springer-Verlag Berlin, 1997, 1992.


Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.