das um 240 v. Chr. von Archimedes von Syrakus gefundene Verfahren zur beliebig genauen Annäherung der Zahl π.

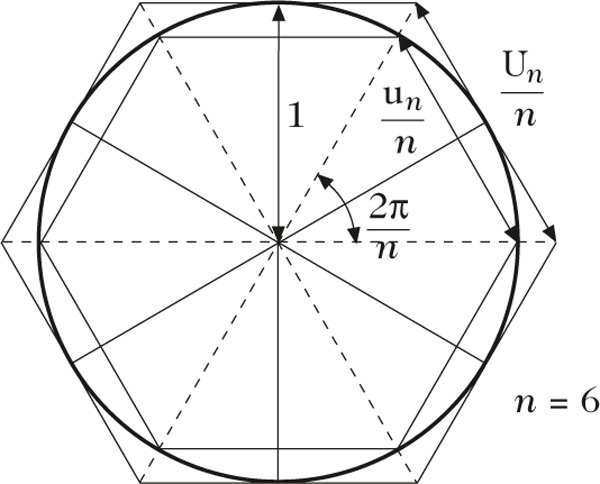
Archimedes betrachtete den Einheitskreis vom Umfang 2π und diesem ein- und umgeschriebene regelmäßige Vielecke: Für den Umfang u_n des einund den Umfang U_n des umgeschriebenen n-Ecks ist u_n< 2π < U_n, und es gilt u_n ↑ 2π und U_n ↓ 2π für n → ∞. Diese Einsichten gehen schon auf Antiphon von Rhamnus und Bryson von Heraclea um 430 v. Chr. zurück, doch entscheidend war Archimedes’ Übergang von n zu 2n Ecken, für den er mit Hilfe geometrischer Überlegungen die Beziehungen \begin{eqnarray}{U}_{2n}=\frac{2{U}_{n}{u}_{n}}{{U}_{n}+{u}_{n}} &, & {u}_{2n}=\sqrt{{U}_{2n}{u}_{n}}\end{eqnarray}

fand, die heute leicht aus \begin{eqnarray}{U}_{n}=2n\tan \frac{\pi }{n} &, & {u}_{n}=2n\sin \frac{\pi }{n}\end{eqnarray}

und den Halbierungsformeln der trigonometrischen Funktionen herzuleiten sind. Archimedes rechnete, beginnend mit einem regelmäßigen Sechseck (u₆ = 3, \begin{eqnarray}{U}_{6}=2\sqrt{3}\end{eqnarray}), mittels geschickter Approximation von Quadratwurzeln durch rationale Zahlen bis zum 96-Eck, was ihm die Abschätzung \begin{eqnarray}3.1408\ldots =3\frac{10}{71}\lt \pi \lt 3\frac{10}{70}=3.1428\ldots \end{eqnarray}

lieferte.

Der Archimedes-Algorithmus ist linear konvergent, und es gilt \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{n\to \infty }\frac{{U}_{2n}-\pi }{{U}_{n}-\pi }=\mathop{\mathrm{lim}}\limits_{n\to \infty }\frac{\pi -{u}_{2n}}{\pi -{u}_{n}}=\frac{1}{4}.\end{eqnarray}

Dieses Verfahren war das erste und, abgesehen vom dazu äquivalenten Cusanus-Algorithmus, etwa neunzehn Jahrhunderte lang das einzige zu einer beliebig genauen Annäherung an π. Es wird wegen seiner historischen Bedeutung und seiner Anschaulichkeit noch heute in der Schule gelehrt.