Lexikon der Mathematik: Arcuscosinusfunktion
Arcuscosinus, die aufgrund der strengen Antitonie und Surjektivität der Cosinusfunktion cos : [0, π] → [−1, 1] zu dieser existierende, streng antitone Umkehrfunktion
\begin{eqnarray}\arccos :[-1,1]\to [0,\pi ].\end{eqnarray}
Für x ∈ ℝ und y ∈ [−1, 1] gilt genau dann cos x = y, wenn
\begin{eqnarray}x=\pm \arccos y+2k\pi \end{eqnarray}
mit einem k ∈ ℤ. Der Graph von arccos ist punktsymmetrisch um (x = 0, \(y=\frac{\pi }{2}\)). Nach dem Satz über die Differentiation der Umkehrfunktion ist arccos differenzierbar in (−1, 1), und für y ∈ (−1, 1) gilt\begin{eqnarray}{\arccos }^{^{\prime} }\(y)=-\frac{1}{\sqrt{1-{y}^{2}}}.\end{eqnarray}
Mit \(\arccos y=\frac{\pi }{2}-\arcsin y\) erhält man aus Eigenschaften der Arcussinusfunktion leicht die Eigenschaften der Arcuscosinusfunktion. Wir erwähnen noch den folgenden Zusammenhang: Für y ∈ [−1, 1] gilt:\begin{eqnarray}\sin (\arccos y)=\sqrt{1-{y}^{2}},\\ \tan (\arccos y)=\frac{\sqrt{1-{y}^{2}}}{y},\end{eqnarray}
letzteres natürlich nur für у ≠ 0.
arccos© Springer-Verlag GmbH Deutschland 2017 Bild vergrößern
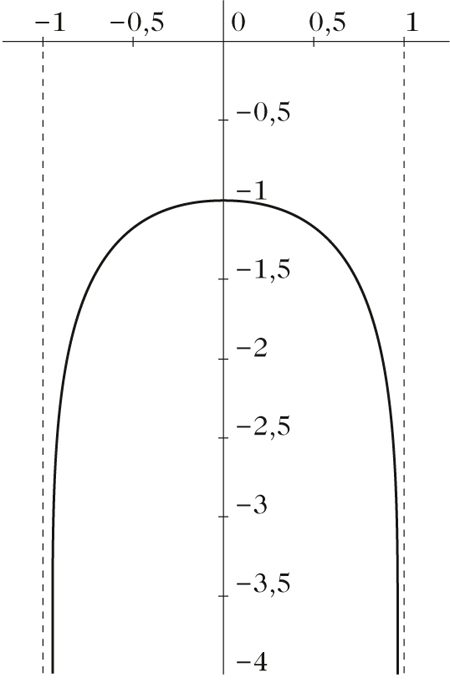
arccos’© Springer-Verlag GmbH Deutschland 2017 Bild vergrößern
Copyright Springer Verlag GmbH Deutschland 2017

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.