Lexikon der Mathematik: Arcustangensfunktion
Arcustangens, die aufgrund der strengen Isotonie und Surjektivität der Tangensfunktion \(\tan :(-\frac{\pi }{2},\frac{\pi }{2})\to {\rm{{\mathbb{R}}}}\) zu dieser existierende, streng isotone Umkehrfunktion
\begin{eqnarray}\arctan :{\rm{{\mathbb{R}}}}\to (-\frac{\pi }{2},\frac{\pi }{2}).\end{eqnarray}
Für \(x\in {\rm{{\mathbb{R}}}}\backslash \{k\pi +\frac{\pi }{2}|k\in {\rm{{\mathbb{Z}}}}\}\) und y ∈ ℝ gilt genau dann tan x = y, wenn\begin{eqnarray}x=\arctan y+k\pi \end{eqnarray}
mit einem k ∈ ℤ. Mit tan ist auch aretan eine ungerade Funktion. Nach dem Satz über die Differentiation der Umkehrfunktion ist aretan differenzierbar, und für y ∈ ℝ gilt\begin{eqnarray}{\arctan }^{^{\prime} }(y)=\frac{1}{1+{y}^{2}}.\end{eqnarray}
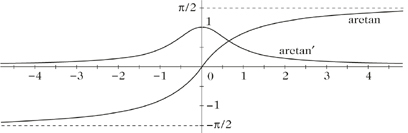
arctan und arctan’
Für y ∈ (−1, 1] hat man die Darstellung durch die Gregoiy-Reihe
\begin{eqnarray}\arctan y=\displaystyle \sum _{n=0}^{\infty }\frac{{(-1)}^{n}}{2n+1}{y}^{2n+1},\end{eqnarray}
was mit y = 1 die Leibniz-Reihe liefert, und woraus man mit\begin{eqnarray}\mathrm{arccot}y=\frac{\pi }{2}-\arctan y\end{eqnarray}
auch eine Darstellung der Arcuscotangensfunktion erhält. Ferner folgt daraus für у > 1 die Reihe\begin{eqnarray}\arctan y=\frac{\pi }{2}-\displaystyle \sum _{n=0}^{\infty }\frac{{(-1)}^{n}}{2n+1}\frac{1}{{y}^{2n+1}}.\end{eqnarray}
Wir erwähnen noch den folgenden Zusammenhang:Für y ∈ ℝ gilt:
\begin{eqnarray}\sin (\arctan y) & = & \frac{y}{\sqrt{1+{y}^{2}}},\\ \cos (\arctan y) & = & \frac{1}{\sqrt{1+{y}^{2}}}.\end{eqnarray}
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.