Lexikon der Mathematik: Assoziationsmaß
Maß zur Beschreibung des Zusammenhangs zwischen zwei Variablen, von denen mindestens eine nominalskaliert ist.
Da im Falle nominalskalierter Variablen die betreffenden Codierungen keiner Ordnungsrelation folgen, sind Korrelationskoeffizienten als Maß ungeeignet. Assoziationsmaße geben den Grad der Abhängigkeit bzw. Unabhängigkeit zwischen den Variablen im allg. durch einem Wert im Intervall [0, 1] an. Ein Wert um 0 bedeutet dabei völlige Unabhängigkeit, ein Wert um 1 größte Abhängigkeit. Assoziationsmaße sind auch für ordinalskalierte Variablen entwickelt worden.
Assoziationsmaße dienen zur Auswertung von Kontingenztafeln. Seien (X, Y) ein Paar diskreter Merkmale mit dem Wertebereich χ = {α1,…, αk} bzw. У = {b1, …, bm} und (xi, yi), i = 1, …, &Ngr; eine Stichprobe von (X, Y).
Typische Maße zur Bewertung der Assoziation von X und Y basieren auf dem χ2-Abstand zur Messung der Unabhängigkeit:
\begin{eqnarray}{\chi }^{2}=\displaystyle \sum _{j=1}^{m}\displaystyle \sum _{i=1}^{k}\frac{{({H}_{ij}^{B}-{H}_{ij}^{E})}^{2}}{{H}_{ij}^{E}},\end{eqnarray}
1. Der Kontingenzkoeffizient:
\begin{eqnarray}c=\sqrt{\frac{{\chi }^{2}}{{\chi }^{2}+N}}.\end{eqnarray}
Offensichtlich ist c < 1. Der maximale Wert von c ist von k und m, d.h, der Zeilen-und Spaltenzahl der Kontingenztafel abhängig. Für eine 3 × 2-Tafel gilt beispielsweise c ≤ 0, 762.Um Kontingenzkoeffizienten zwischen verschiedenen Kontingenztafeln mit unterschiedlichen Feldzahlen vergleichen zu können, wird der korrigierte Kontingenzkoeffizient
\begin{eqnarray}{c}_{korr}=\sqrt{\frac{q}{q-1}}\cdot \sqrt{\frac{{\chi }^{2}}{{\chi }^{2}+N}}\end{eqnarray}
mit q = min{k, m} verwendet, dessen Maximalwert ≈ 1 ist.2. Cramers V-Koeffizient
\begin{eqnarray}V=\sqrt{\frac{{\chi }^{2}}{N(q-1)}}.\end{eqnarray}
V liegt im Bereich zwischen Null und Eins, wobei V den Wert Eins erreichen kann. Für den Spezialfall k = m = 2 bezeichnet man V auch als Phi-Koeffizient ϕ.Andere Assoziationsmaße werden nach dem Konzept der sogenannten proportionalen Fehlerreduktion berechnet.
Assoziationsmaße werden auch für ordinalskalierte Variablen definiert. Alle diese Maße bauen auf der Anzahl der Fehlordnungen (Inversionen I) und richtigen Ordnungen (Proversionen P) auf, die sich ergeben, wenn man die Werte einer der beiden Variablen in aufsteigender Reihenfolge niederschreibt und die Werte der anderen Variablen entsprechend zuordnet. Diese Maße können Werte zwischen −1 und 1 annehmen. Ein typischer Vertreter ist „Kendalls Tau“.
Bei der Auswertung der Assoziationsmaße wendet man durchaus Faustregeln an, so z. B. die Regel, daß ein Wert < 0.2 auf Unabhängigkeit schließen läßt. Bei Werten ≥ 0.5 ist zu beachten, daß der Wert 1 nicht oder nur schwer erreicht wird. Im allgemeinen sollte man stets einen statistischen Test zum Prüfen der Unabhängigkeit von X und Y durchführen (χ2-Unabhängigkeitstest).
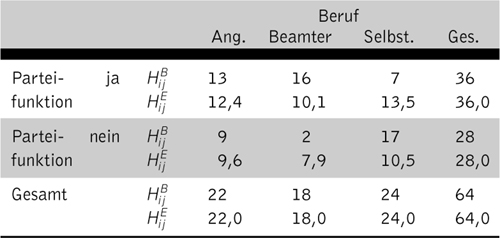
Beispiel. Es soll untersucht werden, ob es einen Zusammenhang zwischen dem Ausüben einer Parteifunktion und dem Beruf gibt. Dazu wurde eine Stichprobe an N = 64 Personen erhoben, die folgende Kontingenztafel ergibt:
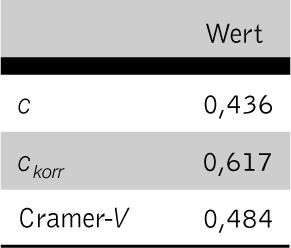
Es ergibt sich ein höchst signifikantes Ergebnis; die Parteifunktionen sind bei den Beamten über-und bei den Selbständigen unterrepräsentiert. Die folgende Tabelle zeigt die Werte einiger Kontingenzkoeffizienten:
Die Werte liegen bei allen Koeffizienten deutlich von der 0 entfernt (> 0.2). Das bedeutet, daß man nicht darauf schließen kann, daß die Ausübung einer Parteifunktion vom Beruf unabhängig ist.
Der χ2-Unabhängigkeitstest bestätigt das Ergebnis.
Schreiben Sie uns!