Kurve, oft eine Gerade, der die Punkte einer anderen Kurve, die durch eine auf ganz ℝ definierte Parametergleichung a(t) gegeben ist, für t → ±∞ beliebig nahe kommen. Die Asymptote kann auch zu einem Punkt entarten.

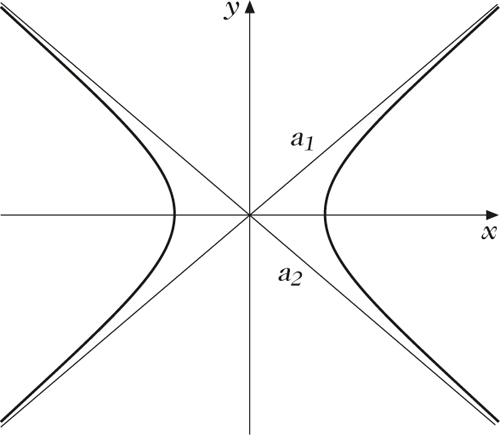
Als Beispiel betrachte man die Asymptoten der Hyperbel; dies sind zwei Geraden a₁ und a₂, denen sich eine Hyperbel für sehr weit vom Mittelpunkt entfernte Punkte beliebig weit annähert, ohne jedoch diese Geraden (im Endlichen) zu erreichen. Ist eine Hyperbel H durch die Gleichung

\begin{eqnarray}\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1\end{eqnarray}

\begin{eqnarray}{y}^{2}={b}^{2}(\frac{{x}^{2}}{{a}^{2}}-1)\end{eqnarray}

\begin{eqnarray}{f}_{1}(x)=b\sqrt{\frac{{x}^{2}}{{a}^{2}}-1}\text{\hspace{1em}}\text{und}\text{\hspace{1em}}{f}_{2}(x)=-b\sqrt{\frac{{x}^{2}}{{a}^{2}}-1}\end{eqnarray}

Die Asymptoten a₁ und a₂ an die Hyperbel H haben daher die Gleichungen

\begin{eqnarray}{a}_{1}:y=\frac{b}{a}\cdot x\text{\hspace{1em}}\text{und}\text{\hspace{1em}}{a}_{2}:y=-\frac{b}{a}\cdot x.\end{eqnarray}