Lexikon der Mathematik: Attraktor
nichtleere abgeschlossene invariante Teilmenge A ⊂ M für ein topologisches dynamisches System (&Mgr;, ℝ, Ф), falls eine Umgebung U von A existiert, für die gilt:
Ein Attraktor ist asymptotisch stabil. Für einen Attraktor A bezeichnet man die Vereinigung aller offenen Umgebungen von A, die (i) und (ii) erfüllen, als sein Bassin.
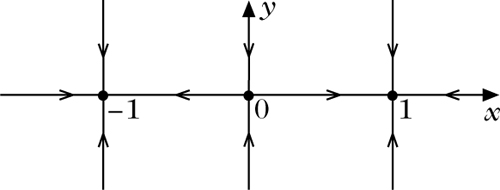
Ein Attraktor kann wegen der topologischen Transitivität nicht weiter in Teil-Attraktoren zerlegt werden. Eine solche Zerlegung ist bei anziehenden Mengen jedoch möglich. Dieser Unterschied wird an folgendem Beispiel deutlich:
Wir betrachten das Differentialgleichungssystem
\begin{eqnarray}{x}^{^{\prime} }=x-{x}^{3}\\ {y}^{^{\prime} }=-y.\end{eqnarray}
[1] Guckenheimer, J.; Holmes, Ph.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer-Verlag New York, 1983.
[2] Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and chaos. Springer-Verlag New York, 1990.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.