eine durch eine Punktemenge von n „Beobachtungen“ (x_i, y_i) mittels Ausgleichsrechnung gezogene Gerade y = ax + b.

Dabei wird die Gerade so gewählt, daß der Abstand der durch die Beobachtungen festgelegten Punkte im ℝ² von der durch die Gerade definierten Kurve im ℝ² für ein vorgegebenes Maß minimiert wird.

Hierzu verwendet man häufig die Methode der kleinsten Quadrate, es wird also die Quadratsumme

\begin{eqnarray}\displaystyle \sum _{i=1}^{n}{({y}_{i}-(a{x}_{i}+b))}^{2}\end{eqnarray}

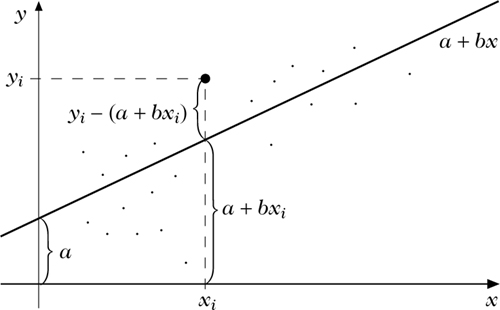
Anschaulich bedeutet dies, daß für jeden Beobachtungspunkt (x_i, y_i) der in vertikaler Richtung genommene Abstand zwischen dem beobachteten Wert y_i und dem auf der Gerade liegenden Wert ax_i + b betrachtet wird. Diese Abstände werden quadriert, aufsummiert und dann miminiert. Es folgt für

\begin{eqnarray}\tilde{x}=\frac{1}{n}\displaystyle \sum _{i=1}^{n}{x}_{i}\text{\hspace{1em}}\text{und}\text{\hspace{1em}}\bar{y}=\frac{1}{n}\displaystyle \sum _{i=1}^{n}{y}_{i},\end{eqnarray}

\begin{eqnarray}a=\frac{\displaystyle {\sum }_{i=1}^{n}({x}_{i}-\bar{x})({y}_{i}-\bar{y})}{\displaystyle {\sum }_{i=1}^{n}{({x}_{i}-\bar{x})}^{2}}\text{\hspace{1em}}\text{und}\text{\hspace{1em}}b=\bar{y}-a\bar{x}.\end{eqnarray}