Lexikon der Mathematik: Bachets Wägeproblem
lautet: Wieviele Gewichte braucht man mindestens, um mit einer Balkenwaage jedes ganzzahlige Gewicht von 1 bis 40 Pfund auswiegen zu können,
- wenn man die Gewichte nur auf eine Waagschale legen darf,
- wenn man beide Waagschalen benutzen darf?
Dieses Wägeproblem wurde schon im 13. Jahrhundert von Fibonacci erwähnt. Bachet beschrieb es in seinem 1612 erschienenen Buch „Problèmes plaisantes et delectables qui se font par les nombres“, weswegen es heute meist als Bachets Wägeproblem bezeichnet wird.
Im ersten Fall geht es darum, eine Menge G = {g1, …, gk}mit folgender Eigenschaft zu finden: Jede ganze Zahl N mit 1 ≤ N ≤ M = 40 läßt sich als Summe einer Auswahl von Gewichten aus G darstellen. Bachet gab die Lösung
Daß dies eine Lösung ist, sieht man wie folgt: Jede natürliche Zahl N ≤ 40 besitzt eine (eindeutig bestimmte) Binärdarstellung
Im zweiten Fall ist eine möglichst kleine Menge B = {b0, …, bk} derart gesucht, daß sich jede natürliche Zahl ≤ M = 40 in folgender Weise darstellen läßt:
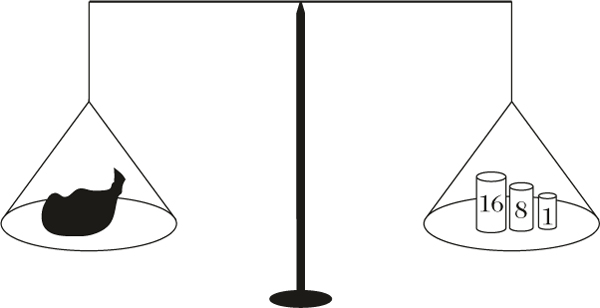
Auswiegen von N = 25 Pfund mit Gewichten zu 16, 8 und 1 Pfund
Dies ist eine Lösung, denn jede ganze Zahl n mit
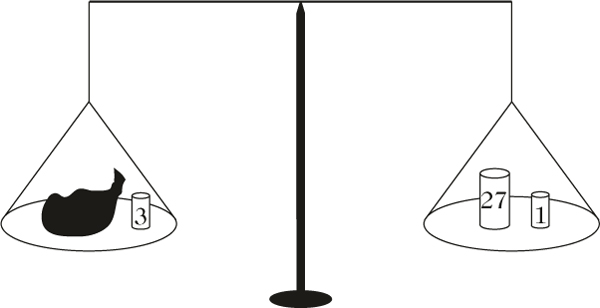
Auswiegen von N = 25 Pfund mit Gewichten zu 27, 3 und 1 Pfund
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.