findet statt an Stellen, wo die betrachteten Funktionen die gleichen Werte und die gleiche Steigung haben.

Genauer: Sind \(f,g:I\to {\rm{{\mathbb{R}}}}\) zwei auf einem Intervall \(I\subset {\rm{{\mathbb{R}}}}\) definierte Funktionen, und ist a ein innerer Punkt von I, in dem f und g differenzierbar sind, dann berühren sich f und g an der Stelle a genau dann, wenn \begin{eqnarray}f(a)=g(a)\,\,\,{\rm{und}}\,\,\,f^{\prime} (a)=g^{\prime} (a).\end{eqnarray}f und g überkreuzen sich in einem Berührungspunkt a genau dann, wenn f − g in a kein lokales Extremum hat. (Die Literatur ist hier nicht ganz einheitlich: Manche Autoren sprechen in einem solchen Fall, also wenn sich die Funktionen überkreuzen, nicht mehr von einer Berührung; die hier gegebene Definition scheint aber die verbreitete).

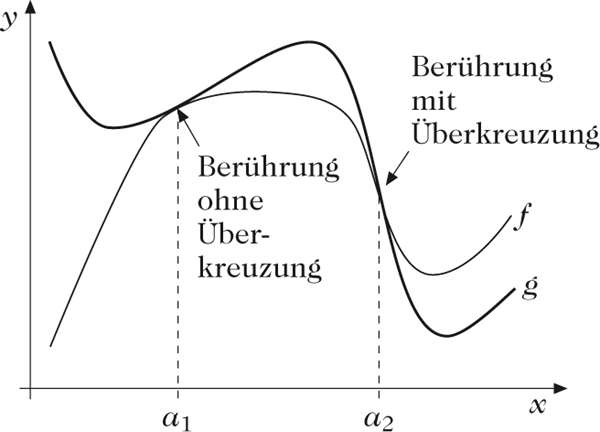
Berührung zweier Funktionen

Allgemeiner sagt man für n ∈ ℕ₀, daß f und g sich an der Stelle a „von n-ter Ordnung berühren“ oder einen Berührungspunkt n-ter Ordnung haben, wenn sie in a n-mal differenzierbar sind, und ihre Ableitungen in a bis zur Ordnung n übereinstimmen, wenn also gilt: \begin{eqnarray}{f}^{(k)}(a)={g}^{(k)}(a)\end{eqnarray} für k = 0, …, n.

Ein Berührungspunkt 0-ter Ordnung ist ein Schnittpunkt, ein Berührungspunkt erster Ordnung ein gewöhnlicher Berührungspunkt, und in einem Berührungspunkt zweiter Ordnung haben die beiden Funktionen auch die gleiche Krümmung.