Lexikon der Mathematik: bestimmtes Integral
liefert den Flächeninhalt der Fläche, die von der x-Achse, den Geraden x = a, x = b und dem Graphen einer Funktion f begrenzt wird. Dabei seien −∞ < a< b< ∞ und f : [a, b] → ℝ beschränkt.
Der unterhalb der x-Achse liegende Anteil wird jeweils mit negativem Vorzeichen versehen:
Vorzeichenverteilung
Die Funktion f heißt integrierbar (über [a, b]) genau dann, wenn es ein A ∈ ℝ gibt mit:
Zu jedem ϵ > 0 existieren eine natürliche Zahl n sowie
\begin{eqnarray}a={x}_{0}\lt {x}_{1}\lt \cdots \lt {x}_{n}=b,\end{eqnarray}
uν, oν ∈ ℝ mit uν ≤ f(x) ≤ oν für xv−1 ≤ x ≤ xν, ν = 1,…,n, und\begin{eqnarray}U:=\displaystyle \sum _{\nu =1}^{n}{u}_{\nu }({x}_{\nu }-{x}_{\nu -1})\le A\le \\ \le \displaystyle \sum _{\nu =1}^{n}{o}_{\nu }({x}_{\nu }-{x}_{\nu -1})=:O\end{eqnarray}
Ein solches U heißt Untersumme, O Obersumme. Das obige A ist eindeutig bestimmt, man schreibt
\begin{eqnarray}\displaystyle \underset{a}{\overset{b}{\int }}f(x)dx:=A.\end{eqnarray}
Diese Bezeichnungsweise – (bestimmtes) Integral von f über [a, b], genauer Riemann-Integral, auch eigentliches Riemann-Integral – geht auf Gottfried Wilhelm Leibniz (1675) zurück.Das Integralzeichen \(\int \) ist aus einem stilisierten S (für Summe) hervorgegangen. Für manche Dinge wäre beispielsweise die Notierung \(\displaystyle {\int }_{a}^{b}f\) sinnvoller, insbesondere da die,Variable‛ x keine Rolle spielt und somit durch irgendeine andere Variable ersetzt werden kann.
Die Funktion f bezeichnet man auch als Integrand, a und b als untere bzw. obere (Integrations-) Grenze und [a, b] als Integrationsintervall.
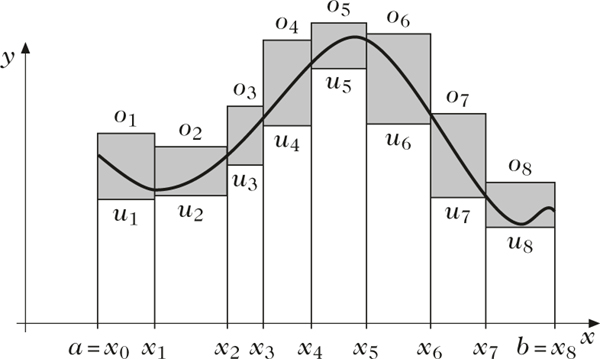
Ober- und Untersummen
Zur Veranschaulichung betrachte man die Abbildung. Der gesuchte Flächeninhalt ist in diesem Beispiel mindestens so groß wie die Summe der Flächen der acht nicht schraffierten Rechtecke
\begin{eqnarray}(\displaystyle \sum _{\nu =1}^{8}{u}_{\nu }({x}_{\nu }-{x}_{\nu -1})=U)\end{eqnarray}
\begin{eqnarray}(U+\displaystyle \sum _{\nu =1}^{8}({o}_{\nu }-{u}_{\nu })({x}_{\nu }-{x}_{\nu -1})=O).\end{eqnarray}
Durch die gegebene Unterteilung ist der gesuchte Flächeninhalt bis auf die O − U, die Summe der Flächeninhalte der acht schraffierten Rechtecke, bestimmt.Wichtigstes Hilfsmittel zur Berechnung bestimmter Integrale ist der Fundamentalsatz der Differential- und Integralrechnung, der die Möglichkeit der Auswertung über Stammfunktionen zeigt.
Damit sind beispielsweise die Substitutionsregeln und die Regel der partiellen Integration auch für das bestimmte Integral zugkräftige Hilfsmittel.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.