Lexikon der Mathematik: Bézier-Fläche
meist über einem dreieckigen Parametergebiet bezüglich einer Basis aus verallgemeinerten Bernstein-Polynomen definierte Fläche.
Zu jedem Tripel (i1, i2, i3) aus der Indexmenge
\begin{eqnarray}I=\{({i}_{1},{i}_{2},{i}_{3})\in {{\mathbb{N}}}_{0}^{3};{i}_{1}+{i}_{2}+{i}_{3}=n\}\end{eqnarray}
Dann ist die zugehörige Bézier-Fläche definiert als die Abbildung
\begin{eqnarray}B(P)=\displaystyle \sum _{({i}_{1},{i}_{2},{i}_{3})\in I}{b}_{({i}_{1},{i}_{2},{i}_{3})}{B}_{({i}_{1},{i}_{2},{i}_{3})}^{n}(P),\end{eqnarray}
wobei P das zugrundegelegte dreieckige Parametergebiet durchläuft.Diese Fläche besitzt die convex-hull-property, und kann mit einer Verallgemeinerung des de Casteljau-Algorithmus ausgewertet werden.
Bézierflâche über einem dreieckigen Parametergebiet mit ihrem Bézier-Netz
In manchen Fällen betrachtet man auch Bézier- Flächen über rechteckigen Parametergebieten. Diese Bézier-Tensorprodukt-Flächen mit Kontrollpunkten bij ∈ ℝ d, i = 0,…,n, j = 0,…,m, sind durch
\begin{eqnarray}B(u,\upsilon )=\displaystyle \sum _{i=0}^{n}\displaystyle \sum _{j=0}^{m}{b}_{ij}{B}_{i}^{n}(u){B}_{j}^{m}(\upsilon )\end{eqnarray}
definiert, wobei die Funktionen \({B}_{i}^{m}\) Bernstein-Polynome darstellen. Man spricht auch von einer Bézierfläche über einem rechteckigen Parametergebiet.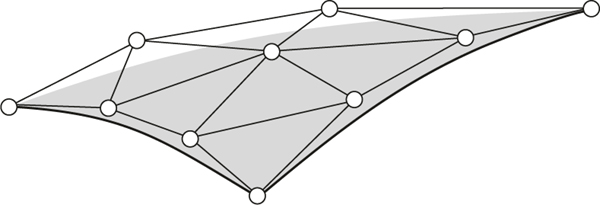
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.