Methode zur Lösung bestimmter Optimierungsprobleme.

Die Methode des branch-and-bound beruht auf dem Prinzip, ein großes Problem aufzuteilen in verschiedene Unterprobleme (Zweige = branches), und das in bestimmter Hinsicht günstigste dieser Unterprobleme zur weiteren Verarbeitung auszuwählen. Dazu ist es nötig, jeden Zweig bewerten zu können, um festzustellen, welcher der zur Auswahl stehenden Zweige der aktuell günstigste ist. Man schätzt dabei im allgemeinen eine Schranke (bound) für die Zielfunktion ab, sodaß man ein Maß für die Güte des aktuellen Zweiges erhält. Das Verfahren führt zu einem Baum, an dem man sowohl die einzelnen Unterprobleme als auch die optimale Lösung ablesen kann. Das Verfahren des branch-and-bound wird auch als Verzweigungsverfahren bezeichnet.

Eine Standardanwendung für branch-and-bound ist das sogenannte Problem des Handlungsreisenden. Man betrachtet dabei einen Handlungsreisenden, der in einer bestimmten Stadt eine Rundreise startet, die ihn durch n − 1 weitere Städte und zum Schluß wieder in die erste Stadt führt. In jeder Stadt will er genau einmal Station machen. Zu bestimmen ist die Reihenfolge der n − 1 anzulaufenden Städte mit dem Ziel, die zurückgelegte Distanz oder aber die Reisekosten oder ähnliches minimal zu halten. Bezeichnet man mit c_ij die Kosten von der i-ten zur j-ten Station, so kann man das Problem präziser mit Hilfe der Matrix

\begin{eqnarray}C=({C}_{11} & {c}_{12} & \cdots & {c}_{1n}\\ {C}_{21} & {c}_{22} & \cdots & {c}_{2n}\\ \vdots & \vdots & & \vdots \\ {C}_{m1} & {c}_{m2} & \cdots & {c}_{mn})\end{eqnarray}

formulieren. Gesucht ist nämlich eine Permutation (i₁, …, i_n) von (1, …, n), so daß \({c}_{{i}_{1},{i}_{2}}+{c}_{{i}_{2},{i}_{3}}+\cdots +{c}_{{i}_{n-1},{i}_{n}}+{c}_{{i}_{n},{i}_{1}}\) minimal wird. Die einfachste Möglichkeit, alle Wege durchzutesten und so den Weg mit dem minimalen Aufwand zu finden, führt zu einer Komplexität von n!, die im allgemeinen nicht akzeptabel ist. Daher kommt hier der branch-and-bound-Ansatz zum Tragen. Man definiert als Kostenabschätzung die Mindestkosten eines Problems P durch

\begin{eqnarray}M(P)=\displaystyle \sum _{i=1}^{n}(\mathop{\min }\limits_{j\ne i}{c}_{ij}+\mathop{\min }\limits_{j\ne i}{c}_{ij})/2,\end{eqnarray}

wobei durch zwei dividiert wird, weil ansonsten jede Kante doppelt gezählt wird. Anhand dieser Mindestkosten beurteilt man dann die verschiedenen Unterprobleme. Hat man beispielsweise das folgende konkrete Problem:

\begin{eqnarray}{P}_{1}=(\infty & 3 & 2 & 7\\ 4 & \infty & 3 & 6\\ 1 & 1 & \infty & 3\\ 1 & 6 & 6 & \infty ),\end{eqnarray}

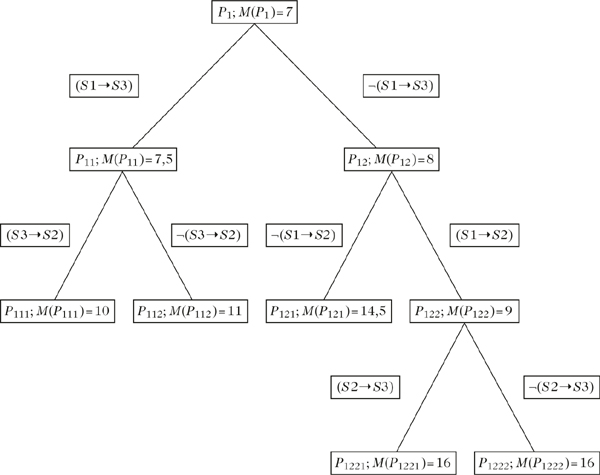
bei dem die Strecken von Station i nach Station i mit Unendlich bewertet werden, um sie von vornherein auszuschließen, so findet man die Mindestkosten \(M({P}_{1})=\frac{1}{2}(3+4+3+4)=7\). Nun kann man mit Station 1 beginnen und annehmen, daß von dort nach Station 3 gefahren wird. Das zugehörige Teilproblem P₁₁ läßt sich wieder mit einer Matrix darstellen und hat die Mindestkosten M(P₁₁) = 7, 5. Die Alternative P₁₂, daß man zwar in Station 1 startet, aber nicht nach Station 3 fährt, hat Mindestkosten von M(P₁₂) = 8. Folglich wird zunächst der Zweig P₁₁ weiterverfolgt. Auf diese Weise erhält man insgesamt den folgenden Baum von Unterproblemen, der schließlich zu den zwei möglichen optimalen Wegen Station 1 – Station 2 – Station 3 – Station 4 bzw. Station 1 – Station 3 – Station 2 – Station 4 führt. Allgemein führt der branch-and- bound-Ansatz beim Problem des Handlungsreisenden zu einer Komplexität von 2ⁿ, was eine deutliche Verbesserung gegenüber n! darstellt.