Lexikon der Mathematik: Carry-Look-Ahead Addierer
kombinatorischer logischer Schaltkreis zur Berechnung der Addition von zwei n-stelligen binären Zahlen α = (αn−1, …, α0) und β = (βn−1, …, β0). Die Idee, den Übertrag
\begin{eqnarray}{c}_{i}:=(\displaystyle \sum _{j=0}^{i}({\alpha }_{j}+{\beta }_{j})\cdot {2}^{j})\text{div}{2}^{i+1}\end{eqnarray}
an der i-ten Stelle effizient zu berechnen, besteht in diesem Verfahren darin, zu einem Block [u : v]\begin{eqnarray}{\alpha }_{u}\ldots {\alpha }_{v}\\ {\beta }_{u}\ldots {\beta }_{v}\end{eqnarray}
\begin{eqnarray}{c}_{i}=1\iff {\gamma }_{i,0}=G\end{eqnarray}
reicht es aus, die Attribute γi,0 für alle i ∈ {n − 1, …, 0} zu berechnen. Um die Attribute γi,0 effizient zu berechnen, nutzt man aus, daß das Attribut γu,v aus den Attributen γu,r+1 und γr,v für einen beliebigen Wert r mit u >r ≥ v mittels des Operators • berechnet werden kann, der durch\begin{eqnarray}\forall X\in \{A,P,G\}A\bullet X=A\\ \forall X\in \{A,P,G\}G\bullet X=G\\ \forall X\in \{A,P,G\}P\bullet X=X\end{eqnarray}
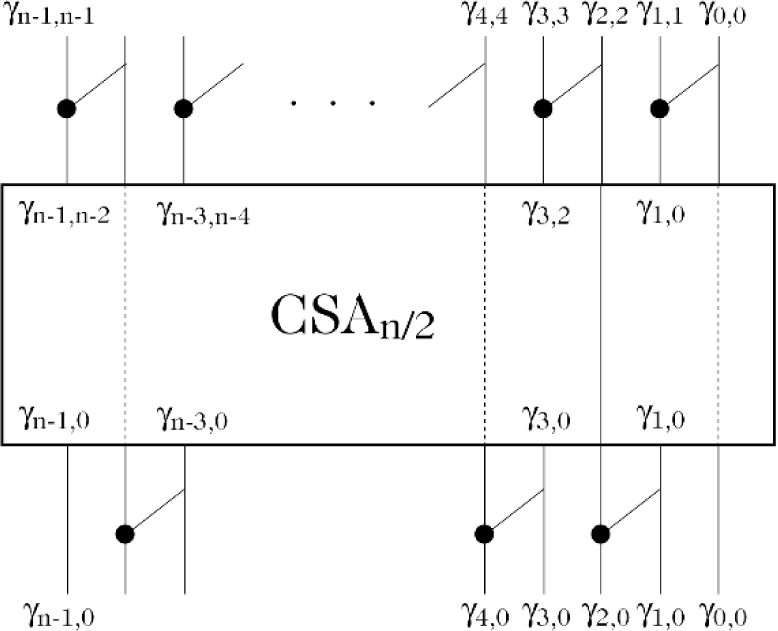
definiert und assoziativ ist. Der linke Operand steht hierbei für das Attribut des linken Blockes [u : r + 1], der rechte Operand für das Attribut des rechten Blockes [r : v]. Die Attribute λi,i der Blöcke der Breite 1 erhält man durch die Überlegung, daß der Block [i : i] genau dann generierend ist, wenn αi = β1 = 1 gilt, genau dann absorbierend ist, wenn αi = βi = 0 gilt, und genau dann propagierend ist, wenn αi ≠ βi ist.Die effiziente Berechnung der Attribute λi,0 (für alle i ∈ {0,…,n − 1} und n = 2k für ein geeignetes k ∈ ℕ) erfolgt durch einen logischen Schaltkreis CLAn. CLAn besitzt n Eingänge und n Ausgänge. Am j-ten Eingang wird ein Attribut aj−1 angelegt. Am j-ten Ausgang wird das Attribut aj−1 • aj−2 • … • a0 berechnet. CLAn kann rekursiv über die folgenden drei Schritte beschrieben werden:
- Berechne γ2j+1,2j = γ2j+1,2j+1 • γ2j,2j für alle \(j\in \{0,\cdots, \frac{n}{2}-1\}\)
- Berechne rekursiv durch Aufruf von \(CL{A}_{\frac{n}{2}}({\gamma }_{n-1,n-2},{\gamma }_{n-3,n-4},\ldots, {\gamma }_{3,2},{\gamma }_{1,0})\) den Vektor \(({\gamma }_{n-1,0},{\gamma }_{n-3,0},\ldots, {\gamma }_{3,0},{\gamma }_{1,0})\)
- Berechne γ2j,0 = γ2j,2j • γ2j−1,0 für alle \(j\in \{0,\cdots, \frac{n}{2}-1\}\).
Berechnung der Attribute beim Carry-Look-Ahead Addierer
Freiheiten bei der Realisierung eines Carry-Look-Ahead Addierers gibt es bei der Codierung der Attribute A, P und G. Wird A durch (0, 0), P durch (0, 1) und G durch (1, 0) codiert, d. h. wird ein Attribut durch zwei Bit g und p codiert, wobei das Bit g das Generate-Bit darstellt, also genau dann 1 ist, wenn das Attribut gleich G ist, und das Bit p das Propagate-Bit darstellt, also genau dann 1 ist, wenn das Attribut gleich P ist, so spricht man von dem Addierer von Brent-Kung. Der Operator • läßt sich in diesem Falle realisieren durch
\begin{eqnarray}({g}_{1},{p}_{1})\bullet ({g}_{2},{p}_{2})=({g}_{1}\vee ({p}_{1}\wedge {g}_{2}),{p}_{1}\wedge {p}_{2}).\end{eqnarray}
Die Laufzeit dieses Addierers verhält sich asymptotisch wie log n, die Fläche wie n log n.
Carry-Ripple Addierer

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.