Lexikon der Mathematik: Chaikin, Algorithmus von
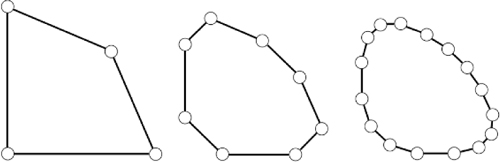
ein affiner stationärer diskreter Unterteilungsalgorithmus für Polygone der folgenden Art. Ist
\begin{eqnarray}{p}_{0},{p}_{1},\ldots {p}_{k},{p}_{k+1}={p}_{0}\in {{\mathbb{R}}}^{n}\end{eqnarray}
ein geschlossenes Polygon, so ist das Polygon \({p}_{0}^{^{\prime} },{p}_{1}^{^{\prime} },\ldots {p}_{2k}^{^{\prime} }\) durchDurch Iteration erhält man eine Folge von Polygonen, die gegen die geschlossene quadratische B-Splinekurve mit Kontrollpunktenp0, p1,… konvergiert.
Für Polygone mit Anfangs- und Endpunkt wird der Algorithmus dort geringfügig modifiziert.
Algorithmus von Chaikin © Springer-Verlag GmbH Deutschland 2017 Bild vergrößern
Copyright Springer Verlag GmbH Deutschland 2017
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.