Allgemeines. Das Simplexverfahren, auch Simplexalgorithmus, 1951 eingeführt von Georg B. Dantzig, ist ein Verfahren zur Minimierung einer linearen Funktion \(x\to {c}^{T}\). x auf einem Polyeder \(M\subseteq {{\mathbb{R}}}^{n}.\)

Es sei M kompakt oder im nicht-negativen Orthanten von \({{\mathbb{R}}}^{n}\) enthalten. Dann besagt der Eckensatz, daß der Minimalwert von \(x\to {c}^{T}.\,\,x\)(falls existent) in einer Ecke von M angenommen wird. Die Idee des Simplexverfahrens besteht darin, von einer Ecke über eine Kante zu einer solchen benachbarten Ecke zu laufen, in der der Zielfunktionswert echt kleiner als in der Ausgangsecke ist. Man setzt dann das Verfahren iterativ fort, diesmal mit der neuen Ecke als Ausgangspunkt. Die Verbindungslinie der beiden beteiligten Ecken nennt man auch eine Abstiegskante.

Falls das lineare Optimierungsproblem lösbar ist, gelangt man nach endlich vielen solcher Ecken- austauschschritte zur optimalen Ecke. Die Bestimmung einer Abstiegskante zu einer (einfachheitshalber nichtentarteten) Ecke läßt sich folgendermaßen realisieren. In einer Umgebung der Ecke wird das Polyeder M in neuen (affin linearen) Koordinaten beschrieben und dadurch in einen nichtnegativen Orthanten transformiert. Dabei gehe die Ecke in den Ursprung sowie die mit ihr inzidierenden Kanten in die jeweiligen Koordinatenachsen des neuen Koordinatensystems über. Man betrachtet jetzt die partiellen Ableitungen der transformierten Zielfunktion im Ursprung. Jede Koordinatenachse, die eine negative partielle Ableitung liefert, entspricht einer Kante, über die die Zielfunktion streng monoton fällt.

Algorithmische Beschreibung

Zur algorithmischen Beschreibung betrachten wir das folgende Standard Lineare Optimierungsproblem (SLO), wobei A eine reelle (m − n)-Matrix vom Rang m sei: \begin{eqnarray}(SOL)\left\{\begin{array}{c}\text{minimiere}\,{c}^{T}\cdot x,x\in M\\ \text{mit}\,M:=\{x\in {{\mathbb{R}}}^{n}|A\cdot x=b,x\ge 0\}.\end{array}\right.\end{eqnarray} Für M in dieser speziellen Form gilt, daß ein zulässiges x genau dann eine Ecke ist, wenn die Spalten von A zu positiven Komponenten von x linear unabhängig sind.

Nichtentartete Ecken

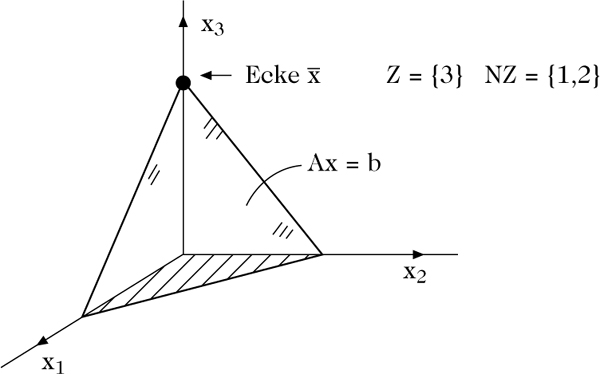
Zunächst beschreiben wir den Eckenaustausch für den Fall einer nichtentarteten Ecke \(\bar{x}\) Es sind dann genau m Komponenten von \(\bar{x}\) positiv. Setze \(Z:=\{i|\bar{{x}_{i}}\gt 0\}\) und \(NZ:=\{1, 2,\mathrm{\ldots},n\}\backslash Z.\) Die Menge Z heißt Basis zur Ecke \(\bar{x}\) und die entsprechenden Komponenten von \(\bar{x}\) Basisvariablen. Ein Vektor \(x\in {{\mathbb{R}}}^{n}\) wird in den Basisanteil x_Z und den Nichtbasisanteil x_NZ aufgeteilt. Analog werden der Zielvektor c und die Matrix A partitioniert. Die Gleichung A · x = b geht dabei in die Gleichung \begin{eqnarray}{A}_{Z}\cdot {x}_{Z}+{A}_{NZ}\cdot {x}_{NZ}=b\end{eqnarray} über. Man beachte, daß die Spalten der quadratischen Matrix A_Z linear unabhängig sind. 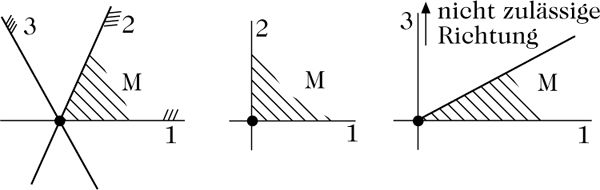Somit kann man x_Z nach x_NZ auflösen (lokale Transformation von M in den nichtnegativen Orthanten von \({{\mathbb{R}}}^{n-m}):\)\begin{eqnarray}{x}_{Z}={A}_{Z}^{-1}\cdot b-{A}_{Z}^{-1}\cdot {A}_{NZ}\cdot {x}_{NZ},\end{eqnarray} wobei \({A}_{Z}^{-1}\cdot b=\bar{{x}_{Z}}.\) Für die Zielfunktion erhält man: \begin{eqnarray}{c}^{T}.x={c}_{Z}^{T}\cdot{x}_{Z}+{c}_{NZ}^{T}\cdot{x}_{NZ}={c}_{Z}^{T}\cdot {A}_{Z}^{-1}\cdot b+{p}^{T}\cdot{x}_{NZ},\end{eqnarray} wobei \begin{eqnarray}p={({p}_{j})}_{j\in NZ}={c}_{NZ}-{A}_{NZ}^{T}\cdot {({A}_{Z}^{-1})}^{T}\cdot c.\end{eqnarray}

Die Komponenten des Vektors p sind gerade die partiellen Ableitungen der transformierten Zielfunktion im Ursprung. Wegen der Konvexität des Optimierungsproblems (SLO) ist die Ecke \(\bar{x}={({\bar{x}}_{Z}^{T},0)}^{T}\) genau dann optimal, wenn p ≥ 0 ist.

Zur numerischen Bestimmung von p (vgl. (4)) muß man im wesentlichen das folgende lineare Gleichungssystem lösen: \begin{eqnarray}{A}_{Z}^{T}\cdot y={c}_{z}.\end{eqnarray} Falls \(\bar{x}\) nicht optimal ist, dann gibt es folglich einen Index \(j\in NZ\,\,\text{mit}\,\,{p}_{j}\lt 0.\) Für die Auswahl eines solchen j kann man mit der Lösung y von (5) nach und nach Spalten der (i. allg. großen) Matrix A_NZ ins Spiel bringen und mit (4) die jeweilige Komponente von p berechnen. Derartige Techniken sind unter den Bezeichnungen column generation technique, revised Simplex method oder Modifizierung des Simplexverfahrens bekannt.

Nachdem der Index j gewählt ist, laufen wir in positiver Richtung der j-ten Koordinate und setzen \begin{eqnarray}{x}_{j}(t):=t\,(t\ge 0),\,{x}_{i}(t):=0,i\in NZ\backslash \{i\}.\end{eqnarray}Mit (2) erhalten wir \begin{eqnarray}{x}_{k}(t)={\bar{x}_{k}\,\,}-t\,\cdot {q}_{k}^{j}\,,\,k\in Z,\,\end{eqnarray} wobei \({q}^{j}:={A}_{Z}^{-1}\cdot \)aⁱ und a^j die entsprechende Spalte von A_NZ ist. Zur numerischen Bestimmung von q^j löst man das folgende lineare Gleichungssystem: \begin{eqnarray}{A}_{Z}\cdot y={a}^{j}.\end{eqnarray}

Falls \({q}^{j}\le 0,\) dann bleiben die Komponenten x_k(t) nichtnegativ für alle t ≥ 0; somit ist ein Halbstrahl in der zulässigen Menge M enthalten, auf dem die Zielfunktion c^T · x nicht nach unten beschränkt ist. Folglich ist (SLO) in diesem Fall nicht lösbar. Sonst ist eine Komponente \({q}_{k}^{j}\gt 0\) für ein k ∈ Z. Es wird nun das maximale t bestimmt, für das alle Basisvariablen nichtnegativ sind: \begin{eqnarray}{t}_{max}:=\mathop{\min}\limits_{k\in Z,{q}_{k}^{j}\gt 0}\left\{\frac{{\bar{x}}_{k}}{{q}_{k}^{j}}\right\}.\end{eqnarray} Das obige Minimum werde etwa in ℓ ∈ Z angenommen. Setze \begin{eqnarray}{Z}{^{\prime}}:=(Z\backslash \{\ell \})\cup \{j\}.\end{eqnarray}

Beachte, daß \({\bar{x}}_{j}\gt 0\) und \({\bar{x}}_{\ell}=0.\) Es zeigt sich, daß die Spaltenvektoren \({a}^{k},k\in {Z}{^{\prime}}\) von A linear unabhängig sind; somit definiert die Indexmenge Z^’ eine neue Ecke. Hiermit ist der Eckenaustausch beschrieben.

Wir bemerken noch, daß in der obigen Durchführung des Eckenaustauschs im wesentlichen zwei Gleichungssysteme ((5) und (6)) gelöst werden müssen. In beiden Systemen tritt die Matrix A_z auf. Die neue Basismatrix A_Z′ unterscheidet sich von A_z nur in einer Spalte. Somit ist \({A}_{{Z}{^{\prime}}}={A}_{Z}+u\cdot {v}^{T},\)wobei u und v Vektoren aus \({{\mathbb{R}}}^{m}\) sind (Rang-1 Update). Es kann nun prinzipiell \({A}_{{Z}{^{\prime}}}^{-1}\) mit Hilfe der sogenannten Sherman-Morrison Formel berechnet werden, sofern \({A}_{Z}^{-1}\) bekannt ist.

Entartete Ecken

Im Falle einer entarteten Ecke \(\bar{x}\) sind r< m Komponenten des Vektors \(\bar{x}\) positiv. Zu den entsprechenden r linear unabhängigen Spalten von A nimmt man dann noch m-r zusätzliche Spalten dazu und formt so eine Basis Z von m linear unabhängigen Vektoren. Jetzt ist allerdings die Basis Z nicht mehr eindeutig bestimmbar. Es ist \(\bar{x}\) genau dann eine optimale Ecke, wenn es dazu eine Basis Z so gibt, daß der entsprechende Vektor p der partiellen Ableitungen (vgl. (4)) nichtnegativ ist. Falls der zu der aktuellen Basis Z gehörende Vektor p negative Komponenten hat, gelangt man wie oben beschrieben an die Stelle, wo t_max zu bestimmen ist (vgl. (7)). Es kann jetzt aber vorkommen, daß t_max = 0 ist (weil nicht alle \({\bar{x}}_{k}\gt 0\) sind). Man führt dann zwar einen Basisaustausch \(Z\to {Z}{^{\prime}}\) aus, bleibt aber in der Ecke x stehen.

So könnte es geschehen, daß man nach einigen solchen Schritten, bei denen man die Ecke \(\bar{x}\) nicht verläßt, zu einer Basis gelangt, die man bereits früher behandelt hat; man läuft dann in einen Zyklus. Mittels einer Zusatzvorschrift läßt sich das Auftreten solcher Zyklen vermeiden. Zum Beispiel könnte man bei der Auswahl der zwei entscheidenden Pivotindizes j und \(\ell \) (vgl. (8)) immer die kleinstmöglichen wählen. Dies ist die sogenannte Strategie von Bland.

Bestimmung einer Startecke

Zur Bestimmung einer Startecke betrachten wir zu (SLO) das folgende höherdimensionale Hilfsproblem (HP) : \begin{eqnarray}(HP)\left\{\begin{array}{l}{\text{Minimiere}\,{y}}_{\text{1}}{{+y}}_{\text{2}}{+}\cdots {{y}}_{{m}}\\ \text{unter den Nebenbedingungen}\\ A\cdot x+y=b,x\ge 0,y\ge 0.\end{array}\right.\end{eqnarray}

Ohne Einschränkung der Allgemeinheit sei b ≥ 0. Man überlegt sich, daß (x, y) := (0, b) eine Ecke für (HP) ist. Ferner kann man zeigen, daß eine nach unten beschränkte lineare Funktion auf einem Polyeder ihr Minimum annimmt. Somit ist (HP) lösbar. Der Simplexalgorithmus, angewandt auf (HP), liefert somit eine optimale Ecke (\(\bar{x}\), \(\bar{y}\)). Falls \(\bar{y}\ne 0\) ist, so ist die zulässige Menge M für (SLO) leer. Falls \(\bar{y}=0\) ist, so ist \(\bar{x}\) eine Ecke für M. Falls in dieser Situation \(\bar{x}\) nichtentartet ist, dann ist die Ausgangsbasis Z für das Simplexverfahren eindeutig bestimmt, ansonsten muß man zur Bestimmung einer solchen Ausgangsbasis so vorgehen, wie es oben bereits im Falle entarteter Ecken beschrieben wurde.

Zur Komplexität des Simplexverfahrens

Im schlechtesten Falle (sogenannte worst-case Analyse) hat der Simplexalgorithmus einen exponentiellen Aufwand. Allerdings zeigte K.H. Borgwardt 1982, daß im Mittel (sogenannte average-case Analyse) ein polynomialer Aufwand erwartet werden kann. Bezüglich auch im schlechtesten Fall polynomialer Algorithmen zur Lösung linearer Optimierungsprobleme vergleiche die Beiträge zu Ellipsoidmethoden und zu Innere-Punkte Methoden.