Lexikon der Mathematik: Dendrit
abgeschlossene zusammenhängende Menge \(E\subset \hat{{\rm{{\mathbb{C}}}}}\) ohne innere Punkte derart, daß auch \(\hat{{\rm{{\mathbb{C}}}}}\backslash E\) zusammenhängend ist.
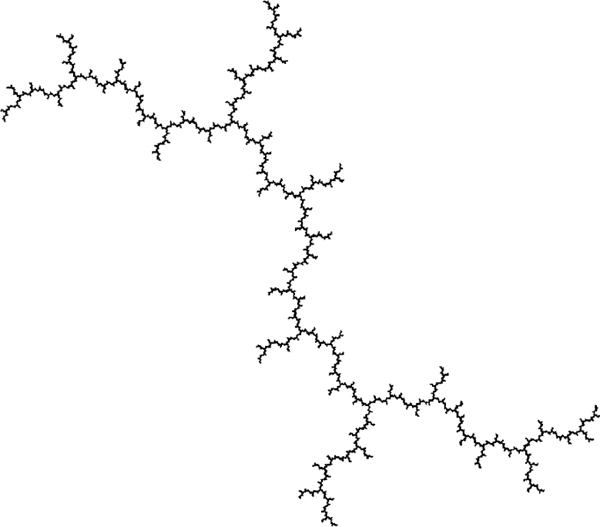
Dendriten treten als Julia-Mengen bei der Iteration rationaler Funktionen auf. Ein einfaches Beispiel ist das Intervall E = [−1, +1]. In der Regel ist die Struktur von Dendriten aber wesentlich komplizierter (s. Abb.).
Ein Dendrit© Springer-Verlag GmbH Deutschland 2017 Bild vergrößern
Copyright Springer Verlag GmbH Deutschland 2017
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.