Eine bestimmte geometrische Teilung einer Strecke, bei der sich die größere Teilstrecke zur kleineren so verhält wie die Gesamtstrecke zum größeren Teil, wird seit etwa dem 19. Jahrhundert als „Goldener Schnitt“ bezeichnet.

Den Zahlenwert dieses Verhältnisses bezeichnet man meist mit dem Buchstaben φ. Die reelle Zahl φ ist die einzige positive Lösung der Gleichung\begin{eqnarray}\phi =1+\frac{1}{\phi },\end{eqnarray} hat also den Wert\begin{eqnarray}\phi =\frac{1}{2}+\frac{1}{2}\sqrt{5}.\end{eqnarray} Die Zahl φ spielt in verschiedenen Teilgebieten der Mathematik eine Rolle, z. B. in der Spieltheorie, in der Graphentheorie, bei dynamischen Systemen, in der Zahlentheorie, und in vielen geometrischen Figuren und Konstruktionen. Daneben findet man den Goldenen Schnitt in zahlreichen biologischen Formationen sowie in Architektur, bildender Kunst, Musik und Poesie.

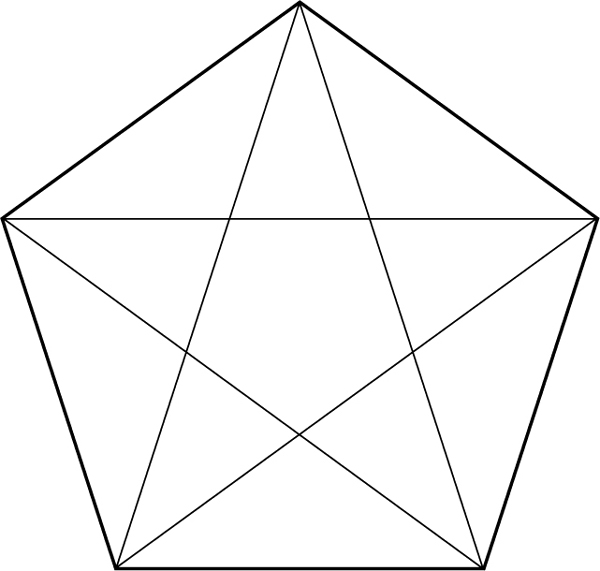
Die Bedeutung dieser Proportion in der Geschichte der Mathematik ist insofern überragend, als anhand des Goldenen Schnitts erstmals die Inkommensurabilität zweier geometrisch konstruierbarer Strecken entdeckt wurde. Dies war eine der überraschendsten und weitreichendsten Entdeckungen der frühen griechischen Mathematik. Der Ursprung liegt darin, daß sich pythagoräische Philosophen sehr stark für regelmäßige Körper, regelmäßige Flächen und Zahlenverhältnisse interessierten. Z.B. ist das Fünfeck wichtig, denn die Oberfläche des Dodekaeders, der „Sphäre aus 12 regelmäßigen Fünfecken”, ist aus diesen Bestandteilen aufgebaut. Man findet nun mit einfachen geometrischen Überlegungen, daß der Schnittpunkt zweier benachbarter Diagonalen im regelmäßigen Fünfeck jede der Diagonalen im Goldenen Schnitt teilt (vgl. Abbildung).

Zeichnet man in das regelmäßige Fünfeck alle fünf Diagonalen ein, so erhält man das sogenannte Pentagramm. Dieses war nicht nur bei den Pythagoräern als Erkennungszeichen in Gebrauch, es hat auch als Drudenfuß eine magische Bedeutung, auf die z. B. in Goethes „Faust“ bei der Einführung des Mephistopheles angespielt wird. Das Pentagramm auf der Schwelle einer Tür schützt vor Dämonen und anderen bösen Kräften, deshalb hatte Mephistopheles als „ein Teil von jener Kraft, die stets das Böse will, und stets das Gute schafft”, gewisse Schwierigkeiten bei der Überwindung des Drudenfußes. (Mephistopheles löste bekanntlich das Problem, indem er einer Ratte befahl, eine Ecke vom Pentagramm abzunagen und so den Zauber unwirksam zu machen.)

In einem Aufsatz, der 1945 in den Annals of Math. erschien, weist der Altphilologe und Mathematikhistoriker Kurt von Fritz unter Anführung zahlreicher Details nach, daß die Inkommensurabilität in der ersten Hälfte des 5. Jahrhunderts v.Chr. entdeckt wurde, und zwar aller Wahrscheinlichkeit nach durch den pythagoräischen Philosophen Hippasos von Metapont anhand des Pentagramms. Hippasos war sehr daran interessiert, die im Pentagramm verborgenen Zahlenverhältnisse zu untersuchen. Er berechnete aufgrund rein geometrischer Überlegungen den Kettenbruch des Verhältnisses φ der Länge einer der Diagonalen zur Länge einer der Seiten des Pentagramms; in heutiger Schreibweise lautet sein Ergebnis:\begin{eqnarray}\phi =1+\frac{1}{1+\frac{1}{1+\ldots }}.\end{eqnarray}

Eine Kettenbruchentwicklung dient dazu, eine Proportion möglichst genau als Verhältnis ganzer Zahlen auszudrücken. Ist die zu untersuchende Proportion rational, so erhält man einen endlichen Kettenbruch. Aber der durch (2) gegebene Kettenbruch ist offenbar nicht endlich, daher ist φ irrational. Geometrisch bedeutet das, daß Diagonale und Seite eines regelmäßigen Fünfecks inkommensurabel sind. Die Zahl φ in (2) ist tatsächlich der Goldene Schnitt, denn die Gleichung (1) folgt sofort aus (2).

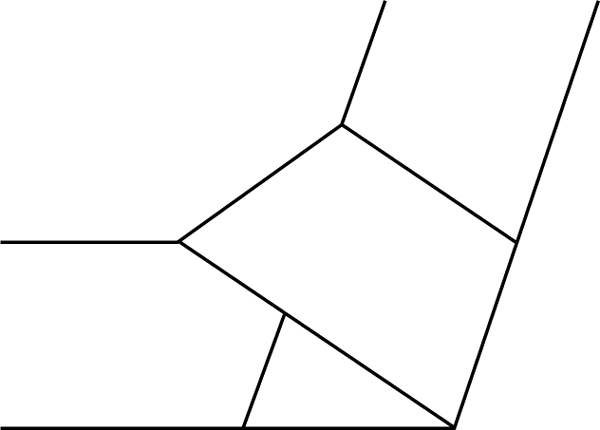
Aufgrund dieser Beziehungen zum Pentagramm läßt sich der Goldene Schnitt recht einfach durch folgende Papierfaltung darstellen: Man nehme einen langen, schmalen Streifen Papier mit gleichmäßiger Breite, mache einen einfachen Knoten, ziehe ihn fest und drücke ihn platt. Man erhält so ein regelmäßiges Fünfeck, von dem eine Diagonale und vier Seiten sichtbar sind [1].

Eine geometrische Konstruktion der Proportion φ mit Zirkel und Lineal findet man bei Euklid. Die lateinischen Übersetzer der Bücher Euklids nannten den Goldenen Schnitt „proportio habens medium et duo extrema”, also „eine Proportion, die eine Mitte und zwei Enden hat”. Bei Kepler findet man die etwas präzisere Bezeichnung „Teilung im äußeren und mittleren Verhältnis”. Zu Beginn des 16. Jahrhunderts benutzte der Venezianer Pacioli, vermutlich als erster, den Namen „divina proportio“ (göttliche Proportion), der in der Folgezeit vielfach verwendet wurde. Daneben gab es auch die profanere Bezeichnung „sectio proportionalis“ (proportionale Teilung) für den Goldenen Schnitt.

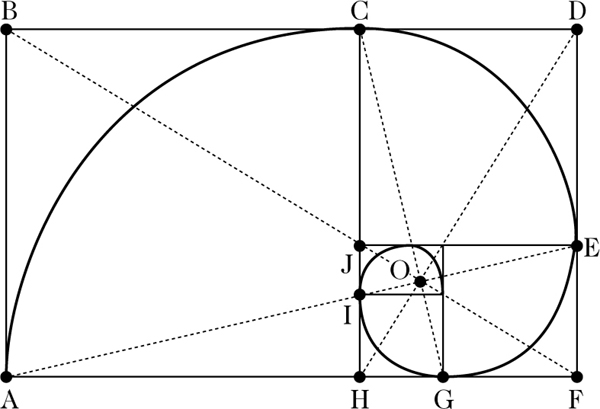
Ein Goldenes Rechteck ist, per definitionem, ein Rechteck mit der Eigenschaft, daß das Verhältnis der größeren zur kleiner Seite gerade der Goldene Schnitt ist. Schneidet man aus einem Goldenen Rechteck R₀ ein Quadrat heraus, so ist das verbleibende Rechteck R₁ wieder golden: das ist gerade die Relation\begin{eqnarray}\phi =\frac{1}{\phi -1},\end{eqnarray} die aus Gleichung (1) herleitbar ist.

Die Goldene Spirale ist eine spezielle logarithmische Spirale. Sie entsteht, indem man zunächst eine (komplexe) Bahnkurve z(t) = e^(a+ib)t ansetzt und dann die reellen Parameter a, b so einstellt, daß nach einer Vierteldrehung t = π/2 aus dem Goldenen Rechteck R₁ gerade das große Goldene Rechteck R₀ wird. Dadurch sind sowohl der Ursprung des Koordinatensystems als auch die Parameter\begin{eqnarray}a=\frac{2\,\mathrm{log}\,\phi }{\pi },\qquad b=1\end{eqnarray} eindeutig festgelegt, und man kommt auf die Gleichung der Goldenen Spirale in Polarkoordinaten (r, ϑ):\begin{eqnarray}r={\phi }^{2\vartheta /\pi }.\end{eqnarray} Bei Kepler findet man eine Approximation der Goldenen Spirale durch Viertelkreise, die den sukzessive aus Goldenen Rechtecken herausgenommenen Quadraten einbeschrieben sind.

Ein Goldenes Dreieck ist ein gleichschenkliges Dreieck mit der Eigenschaft, daß das Verhältnis eines Schenkels zur Basis der Goldene Schnitt ist. Ähnlich wie man aus dem Goldenen Rechteck die Goldene Spirale gewinnt, gewinnt man aus dem Goldenen Dreieck die sogenannte spira mirabilis. Solche logarithmischen Spiralen findet man häufig in der Natur, etwa in Schneckenhäusern oder bei Muscheln. Dies liegt hauptsächlich daran, daß jede logarithmische Spirale eine gewisse Selbstähnlichkeit besitzt: Unter geeigneten Drehstreckungen bleibt sie invariant. Es ist nicht klar, ob ausgerechnet die Goldene Spirale oder die spira mirabilis besonders häufig in der Natur vorkommen.

Ein nachweisbarer Zusammenhang zwischen dem Goldenen Schnitt und biologischen Phänomenen ist durch die Fibonacci-Zahlen\begin{eqnarray}1,1,2,3,5,8,13,21,34,55,89,\ldots \end{eqnarray} gegeben. Diese hängen zusammen mit der Anordnung von Blättern (oder Zweigen, Sprossen, usw.) an einem Stamm oder Stengel.

Beispielsweise zeigen Ulme und Linde eine 1/2-Phyllotaxis („Blattanordnung“), da Zweige und Blätter jeweils abwechselnd an gegenüberliegenden Seiten sprießen. Die Buche etwa zeigt eine 1/3-Phyllotaxis, da man den Blattstand des nächsten Blattes durch eine Drehung um 1/3 einer ganzen Drehung im Uhrzeigersinn erhält; dies entspricht einer Drehung um 2/3 gegen den Uhrzeigersinn. Entsprechend gibt es etwa bei der Eiche eine 2/5-Phyllotaxis, bei der Pappel eine 3/8-Phyllotaxis und bei der Weide eine 5/13-Phyllotaxis. Rechnet man in Drehungen gegen den Uhrzeigersinn, so scheinen bei der Phyllotaxis die Brüche zwischen aufeinanderfolgenden Fibonacci-Zahlen eine Rolle zu spielen:\begin{eqnarray}\frac{1}{2},\frac{2}{3},\frac{3}{5},\frac{5}{8},\frac{8}{13},\ldots \end{eqnarray} Man rechnet nun leicht nach (und kann auch durch vollständige Induktion allgemein beweisen), daß dies gerade die Kehrwerte der Näherungsbrüche der Kettenbruchentwicklung aus Gleichung (2) sind. Daher konvergiert die Folge dieser Brüche gegen φ⁻¹. Was den Zusammenhang zur Botanik betrifft, so gibt es bei manchen Pflanzen(teilen) (z. B. Sonnenblumen, Ananas, Tannenzapfen) ein mathematisches Modell, das das Auftreten der Fibonacci-Zahlen erklärt. Andererseits ist kein allgemeines Naturgesetz bekannt, das dieses Phänomen für jede Pflanzenart wirklich plausibel macht.

Innerhalb verschiedener Teilgebiete der Mathematik taucht der Goldene Schnitt manchmal ziemlich überraschend auf. Ein Beispiel ist das „Einsiedlerspiel“ des britischen Mathematikers Conway: Das Spielfeld ist in kleine quadratische Felder aufgeteilt, und auf jedem Feld steht entweder eine Spielfigur oder nichts. Eine Spielfigur kann eine benachbarte überspringen, wenn das dahinterliegende Feld leer ist, danach wird die übersprungene Figur aus dem Spiel genommen. Zunächst befinden sich alle Spielfiguren unterhalb einer vorher festgelegten horizontalen Linie, dem Rand der „Wüste“. Die Aufgabe ist nun, durch geschicktes Ziehen möglichst weit in die Wüste vorzudringen. Überraschenderweise kann man mit Hilfe des Goldenen Schnitts (und insbesondere unter Verwendung der sofort aus (1) ableitbaren Gleichung φ² = φ+1) beweisen, daß es mit keiner aus endlich vielen Spielfiguren bestehenden Anfangskonfiguration möglich ist, die fünfte Reihe der Wüste zu erreichen.

Ein anderes Beispiel aus der Spieltheorie ist das Zweipersonenspiel von Wythoff [1], in dem man aus dem Goldenen Schnitt eine Gewinnstrategie entwickeln kann.

Ein anderes Teilgebiet der Mathematik, in dem der Goldene Schnitt unvermutet auftaucht, ist die Graphentheorie. Im Zusammenhang mit dem Studium von Färbungen eines Graphen assoziiert man zu jedem Graphen G sein chromatisches Polynom p(G; λ) (ein Polynom in der Unbestimmten λ). Berman und Tutte entdeckten 1969 das Phänomen, daß für jedes chromatische Polynom einerseits\begin{eqnarray}p(G;\phi +1)\ne 0\end{eqnarray} gilt, daß aber andererseits in der Nähe von φ+1 eine Nullstelle von p(G; λ) liegt, falls G eine sog. Triangulierung ist. 1970 konnte Tutte einen Grund dafür finden: er bewies die Abschätzung\begin{eqnarray}|p(G;\phi +1)|\le {\phi }^{5-v}\end{eqnarray} wobei v die Anzahl der Ecken der Triangulierung G bezeichnet. Damit ist für große Eckenzahlen p(G; φ + 1) schon nahe bei 0, also liegt auch in der Nähe eine Nullstelle.

In der Chaos-Theorie findet man beim Studium des Übergangs von Ordnung zum Chaos immer wieder die Fibonacci-Zahlen oder den Goldenen Schnitt. Das liegt in vielen Fällen daran, daß die irrationale Zahl φ besonders schlecht durch rationale Zahlen approximierbar ist. Dieser Sachverhalt läßt sich präzise formulieren und beweisen:

Sei φ der Goldene Schnitt. Dann gilt:

1. Ist ε < 1/\(\sqrt{5}\), so gibt es nur endlich viele Brüche p/q, die die Ungleichung\begin{eqnarray}\left|\phi -\frac{p}{q}\right|\lt \epsilon \cdot \frac{1}{{q}^{2}}\end{eqnarray}erfüllen.
2. Zu jeder irrationalen reellen Zahl x gibt es unendlich viele Brüche p/q mit\begin{eqnarray}\left|x-\frac{p}{q}\right|\lt \frac{1}{\sqrt{5}\cdot {q}^{2}}\cdot \end{eqnarray}
3. Unterscheidet sich die Kettenbruchentwicklung von x in unendlich vielen Gliedern von der Kettenbruchentwicklung (2) des Goldenen Schnitts, so gibt es unendlich viele Brüche p/q mit der Eigenschaft\begin{eqnarray}\left|x-\frac{p}{q}\right|\lt \frac{1}{\sqrt{8}\cdot {q}^{2}}\cdot \end{eqnarray}

In der Architektur wurde der Goldene Schnitt vor allem im antiken Griechenland und in der Renaissance verwendet, Beispiele hierzu findet man in [1]. In der bildenden Kunst ist ebenfalls eine Verwendung des Goldenen Schnitts als Kompositionsprinzip bei manchen Malern sehr wahrscheinlich. Z.B. ist es durchaus plausibel, daß Leonardo da Vinci den Goldenen Schnitt in vielfacher Weise in seinem Gemälde Mona Lisa verwendete. Im allgemeinen zeigt aber das Auffinden der Proportion „Goldener Schnitt“ an einem Gebäude oder in einem Gemälde noch nicht, daß diese Proportion tatsächlich als Konstruktionsprinzip zugrunde lag.

Was die Verwendung des Goldenen Schnitts als Kompositionsprinzip in der Musik betrifft, ist dies wohl in den meisten Fällen im nachhinein hineininterpretiert. Andererseits hat Lendvai in [2] eine sehr detaillierte Analyse der Musik von Béla Bartók vorgelegt, die es nahelegt, daß Bartók bei der Komposition tatsächlich den Goldenen Schnitt als Kompositionsprinzip verwendete.