I. Der Satz des Pythagoras beinhaltet einen grundlegenden Zusammenhang zwischen den Seiten rechtwinkliger Dreiecke:

In jedem rechtwinkligen Dreieck ist der Flächeninhalt des Quadrates über der Hypotenuse gleich der Summe der Flächeninhalte der Quadrate über den Katheten.

Dabei sind die Katheten die dem rechten Winkel benachbarten Seiten und die Hypotenuse die dem rechten Winkel gegenüberliegende Seite des gegebenen rechtwinkligen Dreiecks. Werden die Katheten mit a und b sowie die Hypotenuse mit c bezeichnet, so läßt sich der Satz des Pythagoras durch die Gleichung \begin{eqnarray}{a}^{2}+{b}^{2}={c}^{2}\end{eqnarray}

angeben.

Obwohl der Name des Lehrsatzes auf Pythagoras von Samos zurückgeht, waren diesem Satz vergleichbare Aussagen schon lange vor der Antike, nämlich nachgewiesenermaßen bereits im Babylonischen Reich, bekannt. Nach einer Hypothese B.L. van der Waerdens gab es sogar schon um 3000 v.Chr. wesentliche Bestandteile einer mathematischen Theorie, in denen die Aussage des Satzes des Pythagoras enthalten war (siehe [4]).

II. Beweise für den Satz des Pythagoras

Wegen der großen Bedeutung des Satzes des Pythagoras sind etwa 400 verschiedene Beweise für ihn bekannt (in [1] findet sich eine umfangreiche Zusammenstellung unterschiedlicher Beweismöglichkeiten). Die Idee eines elementaren Beweises ist in Abbildung 2 dargestellt. Die beiden großen Quadrate haben jeweils die Seitenlänge a + b und deshalb gleiche Flächeninhalte (a + b)². Außer den grau eingefärbten Quadraten enthalten diese beiden Quadrate jeweils viermal das Dreieck △ABC. Die weißen Flächen haben also in beiden Quadraten jeweils den gleichen Flächeninhalt. Deshalb muß der Flächeninhalt der grauen Flächen in den beiden großen Quadraten ebenfalls gleich sein. Im linken Bild beträgt der Inhalt der beiden grau eingefärbten Quadrate a² + b² ; der Flächeninhalt des eingefärbten Quadrates im rechten Bild ist c², es gilt also a² + b² = c².

Ein anderer Beweis kann mit Hilfe der Flächeninhaltsformel für rechtwinklige Dreiecke und der binomischen Formeln geführt werden. Im rechten Bild von Abbildung 2 gilt, da der Flächeninhalt der vier Dreiecke jeweils \(\frac{ab}{2}\) beträgt, nämlich \begin{eqnarray}\begin{array}{lll}{c}^{2} & = & {(a+b)}^{2}-4\cdot \frac{ab}{2}\\ & = & {(a+b)}^{2}-2ab={a}^{2}+{b}^{2}.\end{array}\end{eqnarray}

In der analytischen Geometrie kann unter Nutzung des Skalarproduktes ein sehr einfacher vektorieller Beweis für den Satz des Pythagoras geführt werden. Da in einem bei C rechtwinkligen Dreieck ABC die Vektoren \(\overrightarrow{a}=\overrightarrow{CB}\) und \(\overrightarrow{b}=\overrightarrow{CA}\) orthogonal zueinander sind, ist ihr Skalarprodukt Null und es gilt \begin{eqnarray}\begin{array}{ll}{c}^{2} & =\overrightarrow{c}\cdot \overrightarrow{c}=\overrightarrow{AB}\cdot \overrightarrow{AB}={(\overrightarrow{AC}+\overrightarrow{CB})}^{2}={(\overrightarrow{a}-\overrightarrow{b})}^{2}\\ & =\overrightarrow{a}\cdot \overrightarrow{a}+\overrightarrow{b}\cdot \overrightarrow{b}-2\overrightarrow{a}\cdot \overrightarrow{b}=\overrightarrow{a}\cdot \overrightarrow{b}=\overrightarrow{a}\cdot \overrightarrow{a}+\overrightarrow{b}\cdot \overrightarrow{b}={a}^{2}+{b}^{2}\end{array}.\end{eqnarray}

III. Die Satzgruppe des Pythagoras

Eng verwandt mit dem Satz des Pythagoras sind der Höhensatz des Euklid (Euklid, Höhensatz des) und der Kathetensatz:

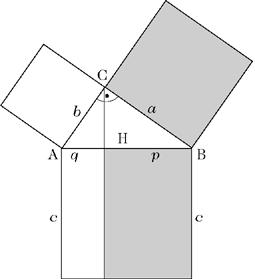
In jedem rechtwinkligen Dreieck hat das Quadrat über einer Kathete den gleichen Flächeninhalt wie das Rechteck, das aus der Hypotenuse und dem der Kathete zugehörigen Hypotenusenabschnitt gebildet wird.

Mit den Bezeichnungen aus Abbildung 3 gilt also a² = p · c und b² = q · c. Der Satz des Pythagoras sowie der Höhen- und der Kathetensatz werden oft zusammenfassend als Satzgruppe des Pythagoras bezeichnet. Der Satz des Pythagoras kann dabei mit Hilfe des (zuvor z. B. unter Ausnutzung von Ähnlichkeitsverhältnissen in zwei rechtwinkligen Teildreiecken zu beweisenden) Kathetensatzes nachgewiesen werden. Aus a² = p · c und b² = q · c folgt nämlich \begin{eqnarray}{a}^{2}\text{}+\text{}{b}^{2}\text{}=\text{}p\text{}\cdot \text{}c\text{}+\text{}q\text{}\cdot \text{}c\text{}=\text{}(p\text{}+\text{}q)\text{}\cdot \text{}c\text{}=\text{}{c}^{2}\text{}.\end{eqnarray}

IV. Anwendungen des Satzes des Pythagoras

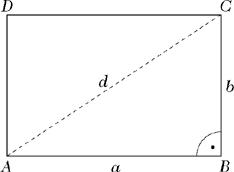
Viele Anwendungen des Satzes des Pythagoras in der Elementargeometrie basieren auf der Zerlegung geometrischer Figuren in rechtwinklige Dreiecke. So läßt sich z. B. die Länge der Diagonalen eines Rechtecks berechnen. Durch Anwendung des Satzes des Pythagoras auf eines der rechtwinkligen Teildreiecke des gegebenen Rechtecks (mit einer Diagonalen als Hypotenuse, siehe Abb. 4) ergibt sich für die Länge d der Diagonale unmittelbar d² = a² + b² bzw. \begin{eqnarray}d=\sqrt{{a}^{2}+{b}^{2}}.\end{eqnarray}

Berechnungen von Rechtecksdiagonalen mit Hilfe einer dem Satz des Pythagoras vergleichbaren Vorschrift wurden bereits im alten Babylon durchgeführt (ca. 1700 v.Chr.). Vielfach wurde der Satz selbst auch nicht als Zusammenhang zwischen Seitenlängen rechtwinkliger Dreiecke, sondern als Zusammenhang zwischen Rechtecksseiten und -diagonalen formuliert.

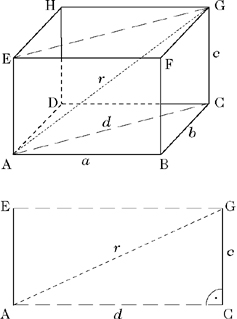
Auch die Länge der Raumdiagonalen eines Quaders kann mit Hilfe des Satzes des Pythagoras bestimmt werden. Für die Länge der Diagonale d eines der begrenzenden Rechtecke des Quaders (Rechteck ABCD in Abb. 5) gilt d² = a² + b². Wird nun der Quader entlang dieser Diagonalen „ zerschnitten“, so entsteht das Rechteck ACGE, dessen Seiten die Höhe c des Quaders und die Diagonale d sind. Die Diagonale dieses Rechtecks ist gerade die Raumdiagonale r des Quaders, für die deshalb nach dem Satz des Pythagoras gilt: \begin{eqnarray}\begin{array}{lll}{r}^{2} & = & {d}^{2}+{c}^{2}={a}^{2}+{b}^{2}+{c}^{2}\text{bzw}\text{.}\\ r & = & \sqrt{{a}^{2}+{b}^{2}+{c}^{2}}.\end{array}\end{eqnarray}

Nach demselben Verfahren wie bei der Berechnung der Diagonalen in Rechtecken und Quadern kann mit Hilfe des Satzes des Pythagoras der Abstand zweier Punkte der Ebene oder des Raumes berechnet werden, deren Koordinaten bezüglich eines kartesischen Koordinatensystems gegeben sind. Die Verbindungsstrecke zweier Punkte P₁ und P₂ kann nämlich als Diagonale eines Rechtecks (in der Ebene) bzw. als Raumdiagonale eines Quaders (im Raum) aufgefaßt werden, dessen Kantenlängen die Differenzen x₂ − x₁, y₂ − y₁ und (nur im Raum)

z₂ − z₁ der Koordinaten der Punkte sind. Für den Abstand zweier Punkte P₁ (x₁ ; y₁) und P₂ (x₂ ; y₂) der Ebene gilt daher \begin{eqnarray}|{P}_{1}{P}_{2}|=\sqrt{{({x}_{2}-{x}_{1})}^{2}+{({y}_{2}-{y}_{1})}^{2}},\end{eqnarray}

und für den Abstand zweier Punkte P₁ (x₁ ; y₁ ; z₁) und P₂ (x₂ ; y₂ ; z₂) des Raumes \begin{eqnarray}|{P}_{1}{P}_{2}|=\sqrt{{({x}_{2}-{x}_{1})}^{2}+{({y}_{2}-{y}_{1})}^{2}+{({z}_{2}-{z}_{1})}^{2}}.\end{eqnarray}

V. Die Umkehrung des Satzes des Pythagoras

Die Umkehrung des Satzes des Pythagoras besagt, daß der durch diesen Satz gegebene Zusammenhang zwischen den Seitenlängen nur in rechtwinkligen Dreiecken besteht:

Wenn für die Seitenlängen a, b und c eines Dreiecks △ABC die Gleichung a² + b² = c²erfüllt ist, so ist dieses Dreieck rechtwinklig, und c ist seine Hypotenuse.

Mit Hilfe der Umkehrung des Pythagoräischen Lehrsatzes läßt sich also anhand der Seitenlängen eines gegebenen Dreiecks ermitteln, ob dieses rechtwinklig ist. Dies ist oft sinnvoll, da sich, beispielsweise bei großen Flächen im Gelände, Abstände leichter und genauer messen lassen als Winkel. Bereits um 2300 v. Chr. wendeten im alten Ägypten die sogenannten Harpedonapten (Seilspanner) pythagoräische Dreiecke an, um nach den zweimal jährlich stattfindenden Überschwemmungen des Nil die Ländereien wieder rechtwinklig abzustecken. Dazu benutzten sie Seile mit zwölf gleich langen Abschnitten, die durch Knoten markiert waren, und spannten daraus Dreiecke mit Seitenlängen von 3, 4 und 5 Seilabschnitten. Da = 3² + 4² = 5² gilt, sind derartige Dreiecke rechtwinklig.

VI. Verallgemeinerungen des Satzes des Pythagoras

Die bekannteste Verallgemeinerung des Satzes des Pythagoras ist der Cosinussatz, der für beliebige (schiefwinklige) Dreiecke gilt. Dieser Satz beinhaltet sowohl die Aussage des Satzes des Pythagoras als auch dessen Umkehrung: Ist ein Dreieck rechtwinklig, so ist der Cosinus eines der Winkel (der hier als γ bezeichnet sei) Null, und die Gleichung \begin{eqnarray}{c}^{2}={a}^{2}+{b}^{2}-2ab\cdot \cos \gamma \end{eqnarray}

des Cosinussatzes nimmt die Gestalt des Satzes des Pythagoras an; gilt umgekehrt z. B. a² + b² = c², so muß der Cosinus des der Seite c gegenüberliegenden Winkels Null, der Winkel selbst also ein Rechter sein.

Eine weitere Verallgemeinerung des Satzes des Pythagoras auf beliebige (nicht notwendig rechtwinklige) Dreiecke ist der Satz von Pappos:

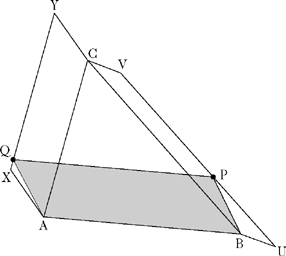
Es sei △ABC ein beliebiges Dreieck und ABPQ ein beliebiges Parallelogramm über der Dreieckseite \(\overline{AB}\)AB, das von der Geraden AB aus auf derselben Seite liegt wie der Punkt C.

Dann ist der Flächinhalt des Parallelogramms ABPQ gleich der Summe der Flächeninhalte zweier Parallelogramme BCUV und ACXY, die über den anderen beiden Dreieckseiten liegen, und deren BC bzw. AC gegenüberliegende Seiten durch die Eckpunkte P bzw. Q des Parallelogramms ABPQ verlaufen.

Ist das Dreieck △ABC bei C rechtwinklig und werden, als spezielle Parallelogramme, Quadrate betrachtet, so geht der Satz von Pappos in den Satz des Pythagoras über.

VII. Pythagoräische Zahlentripel

Rechtwinklige Dreiecke mit ganzzahligen Längen aller drei Seiten werden als pythagoräische Dreiecke, die Zahlenwerte der Seitenlängen solcher Dreiecke als pythagoräische Zahlentripel bezeichnet. Ein pythagoräisches Zahlentripel ist also ein Tripel (a; b; c) dreier natürlicher Zahlen a, b und c, für die a² +b² = c² gilt. Die bekanntesten pythagoräischen Zahlentripel sind (3; 4; 5), (6; 8; 10) und (5; 12; 13). Werden alle drei Zahlen eines pythagoräischen Zahlentripels mit derselben (beliebigen) natürlichen Zahl k multipliziert, so entsteht wieder ein pythagoräisches Zahlentripel, denn es gilt \begin{eqnarray}{(ka)}^{2}\text{}+\text{}{(kb)}^{2}\text{}=\text{}{k}^{2}({a}^{2}\text{}+\text{}{b}^{2})\text{}=\text{}{(kc)}^{2}\text{}.\end{eqnarray}

Allein daraus ergibt sich bereits, daß es unendlich viele pythagoräische Zahlentripel gibt.

Bei der Existenz unendlich vieler pythagoräischer Zahlentripel liegt natürlich die Frage nahe, ob auch Tripel natürlicher Zahlen (a; b; c) existieren, für die aⁿ + bⁿ = cⁿ mit n > 2 gilt. Erstaunlicherweise gibt es für keine natürliche Zahl n, die größer als 2 ist, ein solches Zahlentripel. Der Beweis dieser bereits um 1637 von Fermat behaupteten Tatsache war sehr lange eines der größten Probleme der Mathematik und gelang vollständig erst 1995 dem britischen Mathematiker Andrew Wiles. Siehe hierzu den Artikel zur Fermatschen Vermutung.

[2] Lietzmann, W.: Der pythagoreische Lehrsatz. 9. Auflage, B. G. Teubner Verlagsgesellschaft Leipzig, 1968.

[3] Lietzmann, W.: Von der pythagoreischen Gleichung zum Fermatschen Problem. B.G. Teubner Verlagsgesellschaft Leipzig und Berlin, 1937.

[4] Waerden, B. L. van der: Geometry and Algebra in Ancient Civilizations. Springer Berlin, 1983