das Problem, die Determinante einer Matrix auf effiziente Weise zu berechnen.

Dies löst man meist mittels des Entwicklungssatzes von Laplace. Für eine (n × n)-Matrix A gilt für jedes i ∈ {1, …, n} \begin{eqnarray}\det A=\displaystyle \sum _{j=1}^{n}{(-1)}^{i+j}{a}_{ij}\det {A}_{ij}^{^{\prime} }.\end{eqnarray}

Man nennt dies die Entwicklung nach der i-ten Zeile. Entsprechend gilt für jedes j ∈ {1, …, n} \begin{eqnarray}\det A=\displaystyle \sum _{i=1}^{n}{(-1)}^{i+j}{a}_{ij}\det {A}_{ij}^{^{\prime} },\end{eqnarray}

dies nennt man die Entwicklung nach der j-ten Spalte. Dabei bezeichnet \({A}_{ij}^{^{\prime} }\) die Matrix, welche man aus A durch Streichen der i-ten Zeile und der j-ten Spalte aus A enthält.

Wir illustrieren die Vorgehensweise anhand eines Beispiels: Die Berechnung einer Determinante nach dieser Formel erfolgt für eine (4 × 4)-Matrix z. B. bei Entwicklung nach der zweiten Spalte wie folgt: \begin{eqnarray}\det & \left(\begin{array}{cccc}{a}_{11} & {a}_{12} & {a}_{13} & {a}_{14}\\ {a}_{21} & {a}_{22} & {a}_{23} & {a}_{24}\\ {a}_{31} & {a}_{32} & {a}_{33} & {a}_{34}\\ {a}_{41} & {a}_{42} & {a}_{43} & {a}_{44}\end{array}\right)=\\ & -{a}_{12}\det \left(\begin{array}{ccc}{a}_{21} & {a}_{23} & {a}_{24}\\ {a}_{31} & {a}_{33} & {a}_{34}\\ {a}_{41} & {a}_{43} & {a}_{44}\end{array}\right)\\ & -{a}_{22}\det \left(\begin{array}{ccc}{a}_{11} & {a}_{13} & {a}_{14}\\ {a}_{31} & {a}_{33} & {a}_{34}\\ {a}_{41} & {a}_{43} & {a}_{44}\end{array}\right)\\ & -{a}_{32}\det \left(\begin{array}{ccc}{a}_{11} & {a}_{13} & {a}_{14}\\ {a}_{21} & {a}_{23} & {a}_{24}\\ {a}_{41} & {a}_{43} & {a}_{44}\end{array}\right)\\ & +{a}_{42}\det \left(\begin{array}{ccc}{a}_{11} & {a}_{13} & {a}_{14}\\ {a}_{21} & {a}_{23} & {a}_{24}\\ {a}_{31} & {a}_{33} & {a}_{34}\end{array}\right)\end{eqnarray}

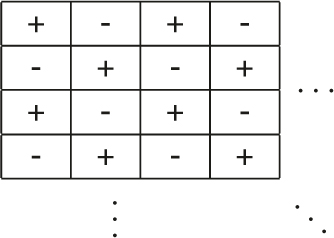
Die durch den Faktor (−1)^i+j bewirkte Vorzeichenverteilung kann man sich als Schachbrettmuster vorstellen:

Im folgenden sind die Determinanten der (3 × 3)-Matrizen zu berechnen. Dies kann entweder wieder mit Hilfe des Entwicklungsatzes von Laplace oder mittels der Regel von Sarrus geschehen. Diese Regel gilt nur zur Berechnung der Determinante einer (3 × 3)-Matrix A.

Dazu schreibt man den ersten und zweiten Spaltenvektor noch einmal „hinter“ die Matrix: \begin{array}{a}_{11} & {a}_{12} & {a}_{13} & {a}_{11} & {a}_{12}\\ {a}_{21} & {a}_{22} & {a}_{23} & {a}_{21} & {a}_{22}\\ {a}_{31} & {a}_{32} & {a}_{33} & {a}_{31} & {a}_{32}.\end{array} Nun bildet man die Summe der Produkte aller längs der „Hauptdiagonalen“ und ihrer Parallelen stehenden Elemente und subtrahiert die Summe der Produkte aller längs der „Antidiagonalen“ und ihrer Parallelen stehenden Elemente: \begin{eqnarray}\det A & = & {a}_{11}{a}_{22}{a}_{33}+{a}_{12}{a}_{23}{a}_{31}+{a}_{13}{a}_{21}{a}_{32}\\ & & -({a}_{31}{a}_{22}{a}_{13}+{a}_{32}{a}_{23}{a}_{11}+{a}_{33}{a}_{21}{a}_{12}).\end{eqnarray}

Der Wert der Determinante einer (2 × 2)-Matrix läßt sich leicht ablesen \begin{eqnarray}\det \left(\begin{array}{cc}{a}_{11} & {a}_{12}\\ {a}_{21} & {a}_{22}\end{array}\right)={a}_{11}{a}_{22}-{a}_{12}{a}_{21}.\end{eqnarray}

Zweckmäßigerweise werden die zu berechnenden Determinanten mit Hilfe der im folgenden noch einmal zusammengestellten Rechenregeln für Determinanten so umgeformt, daß möglichst viele Elemente zu Null werden.

• Für die Multiplikation der Determinante mit einer Zahl λ gilt det(λA) = λⁿ\begin{eqnarray}\det (\lambda A)={\lambda }^{n}\det A.\end{eqnarray}
• Entsteht B durch eine Zeilenvertauschung aus A, dann gilt \begin{eqnarray}\det B=-\det A.\end{eqnarray}
• Entsteht B aus A mittels Addition oder Subtraktion (eines Vielfachen) irgendeiner Zeile zu/von einer anderen oder mittels Addition oder Subtraktion einer Linearkombination einiger Zeilen zu/von einer anderen Zeile, dann gilt \begin{eqnarray}\det B=\det A.\end{eqnarray}
• Für die Multiplikation zweier Determinanten gilt \begin{eqnarray}\det (AB)=(\det A)(\det B).\end{eqnarray}
• Für die Determinante der Inversen von A gilt \begin{eqnarray}\det {A}^{-1}={(\det A)}^{-1}.\end{eqnarray}
• Die Determinante der Summe zweier Matrizen ist im allgemeinen nicht gleich der Summe der Determinaten, d. h. im allgemeinen gilt \begin{eqnarray}\det (A+B)\ne \det A+\det B.\end{eqnarray}
• det A = 0 gilt genau dann, wenn der Rang von A kleiner als n ist; d. h. wenn die Zeilenvektoren von A linear abhängig sind. In diesem Fall besteht eine Zeile von A aus Nullen, zwei Zeilen sind einander gleich, oder eine Zeile ist eine Linearkombination anderer Zeilen.
• Die Determinante einer Dreiecksmatrix ist gerade das Produkt der Diagonalelemente \begin{eqnarray}\det \left(\begin{array}{cccc}{a}_{11} & {a}_{12} & \ldots & {a}_{1n}\\ 0 & {a}_{22} & \ldots & {a}_{2n}\\ \vdots & \ddots & \ddots & \vdots \\ 0 & \ldots & 0 & {a}_{nn}\end{array}\right)={a}_{11}{a}_{22}\ldots {a}_{nn}.\end{eqnarray}

Die Determinantenberechnung für Matrizen höherer Dimension sollte numerisch nicht wie beschrieben erfolgen. Ein gutes Verfahren hier besteht aus den folgenden zwei Schritten. Zunächst berechnet man die LR-Zerlegung der Matrix A\begin{eqnarray}PA=LR,\end{eqnarray} wobei L eine untere, R eine obere Dreiecksmatrix und P eine Permutationsmatrix ist.

Für die Determinante von A gilt dann \begin{eqnarray}\det A & = & {(\det P)}^{-1}(\det L)(\det R)\\ & = & {(-1)}^{r}{l}_{11}{l}_{22}\cdots {l}_{nn}{r}_{11}{r}_{22}\cdots {r}_{nn},\end{eqnarray} wobei die l_ii und r_ii die Diagonalelemente von L bzw. R sind. Da L und R Dreiecksmatrizen sind, lassen sich ihre Determinanten sofort ablesen.

Für det P gilt hier gerade det P = (−1)^r, wobei r die Anzahl der bei der Berechnung der LR-Zerlegung verwendeten Zeilenvertauschungen ist.