in abstrakter Definition die Punktmenge \begin{eqnarray}B=\{p\in {{\mathbb{R}}}^{2}|\Vert p\Vert \lt 1\},\end{eqnarray} also der Spezialfall n = 2 der Einheitskugel.

Zumeist nimmt man jedoch auch noch den Spezialfall der euklidischen Norm an; der Einheitskreis ist also die Menge \({\mathbb{E}}\) der Punkte des ℝ² mit einem euklidischen Abstand kleiner als 1 vom Nullpunkt, also die offene Einheitskreisscheibe \begin{eqnarray}{\mathbb{E}}=\{(x,y)\in {{\mathbb{R}}}^{2}|{x}^{2}+{y}^{2}\lt 1\}.\end{eqnarray}

Die Menge \begin{eqnarray}\bar{{\mathbb{E}}}=\{(x,y)\in {{\mathbb{R}}}^{2}|{x}^{2}+{y}^{2}\le 1\}\end{eqnarray} ist die abgeschlossene Einheitskreisscheibe, und der Einheitskreisrand \begin{eqnarray}\partial {\mathbb{E}}=\{(x,y)\in {{\mathbb{R}}}^{2}|{x}^{2}+{y}^{2}=1\}\end{eqnarray} ist gerade die zweidimensionale Einheitssphäre S¹. Identifiziert man ℝ², versehen mit dem euklidischen Abstand, mit (ℂ, | |), so gilt: \begin{eqnarray}\begin{array}{rll}{\mathbb{E}} & = & \{z\in {\mathbb{C}}||z|\lt 1\},\\ \bar{{\mathbb{E}}} & = & \{z\in {\mathbb{C}}||z|\le 1\},\\ {S}^{1} & = & \{z\in {\mathbb{C}}||z|=1\}.\end{array}\end{eqnarray}

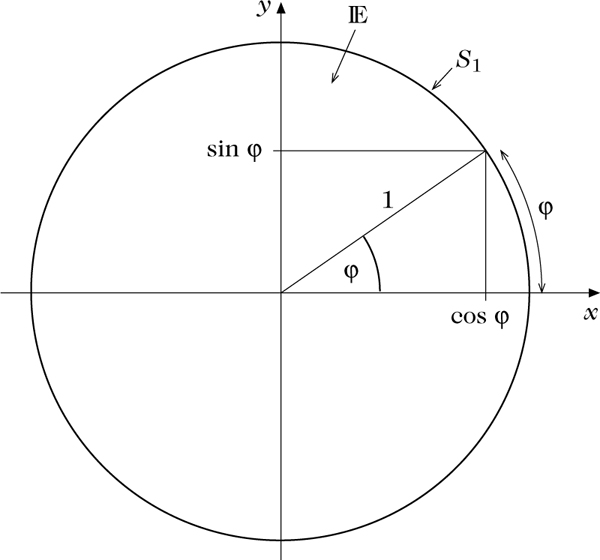
Für einen Punkt (x, y) ∈ S¹ gilt für den Winkel (ϕ ∈ [0, 2π) der Strecke {t(x, y) : t ∈ [0, 1]} zur positiven x-Achse: \begin{eqnarray}\cos \varphi =x \quad,\quad\sin \varphi =y\end{eqnarray}

ϕ ist gleich der Länge des Einheitskreisbogens zwischen (1, 0) und (cos ϕ, sin ϕ).

Wenn ϕ den Bereich [0, 2π) durchläuft, durchläuft (cos ϕ, sin ϕ) den Einheitskreis genau einmal im mathematisch positiven Sinn, also gegen den Uhrzeigersinn, beginnend im Punkt (1, 0).

Insbesondere hat der Einheitskreis den Umfang 2π, und es gilt \begin{eqnarray}{S}^{1}=\{(\cos \varphi, \sin \varphi )|\varphi \in [0,2\pi )\}.\end{eqnarray}

Sieht man S¹ wieder als Teilmenge von ℂ, so zeigt die Eulersche Formel exp(iϕ) = cos ϕ + i sin ϕ: \begin{eqnarray}{S}^{1}=\{\exp (i\varphi )|\varphi \in [0,2\pi )\}\end{eqnarray}

Mit Hilfe der Identität exp(0) = 1, des Additions-theorems der Exponentialfunktion und der 2πi-Periodizität der Exponentialfunktion folgt, daß die Abbildung \begin{eqnarray}f:{\mathbb{R}}\to {S}^{1}\quad,\quad\varphi \mapsto \exp (i\varphi )\end{eqnarray} ein 2π-periodischer Epimorphismus der Gruppe (ℝ, +) auf die Gruppe (S¹, ·) ist.

Es sei abschließend noch darauf hingewiesen, daß die Notation in der Literatur zuweilen nicht ganz einheitlich ist; so versteht man unter dem Einheitskreis manchmal auch gerade das, was wir hier als den Rand des Kreises bezeichnet haben, also die Menge S¹.

Um vor solchen Unsicherheiten geschützt zu sein, findet man manchmal auch die präziseren Bezeichnungen Einheitskreisscheibe (für \({\mathbb{E}}\)) und Einheitskreislinie (für S¹). Ähnliches empfiehlt sich bei der Einheitskugel.