Direkt zum Inhalt

Lexikon der Mathematik: Ellipsoidmethoden

Die Ellipsoidmethoden bilden eine Klasse von Verfahren zur Lösung linearer (und konvexer) Optimierungsprobleme. Grundidee ist dabei die folgende: Zunächst wird das Optimierungsproblem umformuliert als Entscheidungsproblem, ob ein Polyeder \begin{eqnarray}P=\{x|A\cdot x\le b\}\end{eqnarray} nicht-leer ist. Dies geschieht durch Anwendung des Dualitätssatzes der linearen Optimierung.

Dabei werden ein primales Problem \begin{eqnarray}{c}^{T}\cdot v\to \min \,,\,\,E\cdot v\ge f,\,\,v\ge 0\end{eqnarray} und das zugehörige duale Problem \begin{eqnarray}{d}^{T}\cdot y\to \max \,,\,\,{E}^{T}\cdot y\le c,\,\,y\ge 0\end{eqnarray} zum System \begin{eqnarray}-E\cdot v\le -f,-v\le 0,\\ {E}^{T}\cdot y\le c,-y\le 0,\\ {c}^{T}\cdot v-{d}^{T}\cdot y\le 0\end{eqnarray} zusammengefaßt. Dies liefert dasP definierende System A · x ≤ b (mit x := (v, y) und entsprechender Festsetzung von A und b).

Die Äquivalenz der Aufgabe, für dieses Problem einen zulässigen Punkt zu finden, zur ursprünglichen Optimierungsaufgabe folgt daraus, daß die DualitätslückecT · x − bT · y nur in Extremalpunkten verschwindet, aber sonst positiv ist.

Das eigentliche Verfahren beginnt nun mit der Konstruktion eines speziellen Ellipsoids E0 = (z0, B0). Dabei heißt eine Teilmenge E(z, B) des ℝn ein (spezielles) Ellipsoid mit Mittelpunkt z ∈ ℝn, falls sie in der Form \begin{eqnarray}\{x\in {{\mathbb{R}}}^{n}|{(x-z)}^{T}\cdot {B}^{-1}\cdot (x-z)\le 1\}\end{eqnarray} schreibbar ist. Hierbei sei B eine positiv definite (n, n)-Matrix. Das erste Ellipsoid E0 wird dabei so gewählt, daß es im Fall P ≠ ∅ einen Lösungspunkt von P enthält (s. unten).

Nun wird schrittweise eine Familie {Ei(zi, Bi)}i, 1 ≤ i ≤ s von Ellipsoiden konstruiert, die folgende Eigenschaften erfüllt:

  • Ei(zi, Bi) ∩ P ⊆ Ei+1(zi+1, Bi+1) ∩ P; diese Bedingung besagt, daß man beim Übergang von Ei zu Ei+1 keinen der bereits eingefangenen Punkte von P verliert.
  • Falls P ≠ ∅, so gilt P ∩ Es(zs, Bs) ≠ ∅; im Falle der Lösbarkeit enthält also Es eine Lösung.
  • Das Verhältnis der Volumina \begin{eqnarray}\frac{\text{vol}({E}_{i+1})}{\text{vol}({E}_{i})}\end{eqnarray} zweier aufeinanderfolgender Ellipsoide ist kleiner einer festen Konstanten λ < 1, die lediglich von der Raumdimension n, aber nicht von den Daten des Ausgangsproblems abhängt. (Man beachte, daß λ asymptotisch für wachsendes n gegen 1 strebt.)

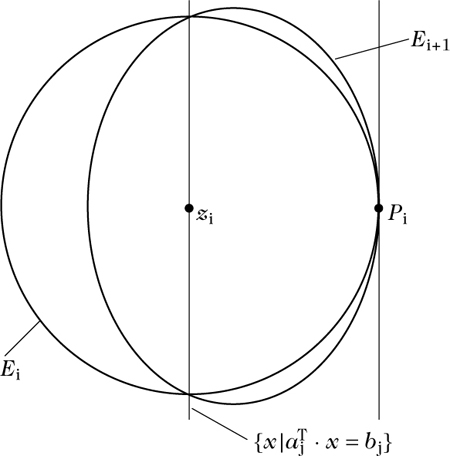
    Zur Konstruktion von Ei+1 aus Ei betrachtet man den Mittelpunkt zi von Ei und prüft, ob zi ∈ P. Falls dies zutrifft, so ist das Entscheidungsproblem positiv beantwortet. Andernfalls findet man eine Ungleichung \({a}_{j}^{T}\cdot x\le {b}_{j}\) von P, die von zi verletzt wird. Nun wird die Hyperebene \(\{x|{a}_{j}^{T}\cdot x={b}_{j}\}\) in Richtung des Halbraums \(\{x|{a}_{j}^{T}\cdot x\ge {b}_{j}\}\) parallel verschoben, bis sie Ei noch in einem Punkt Pi tangiert. Man wählt dann z. B. Ei+1 als dasjenige Ellipsoid minimalen Volumens, das \begin{eqnarray}{E}_{i}\cap \{x|{a}_{j}^{T}\cdot x\ge {a}_{j}^{T}\cdot {z}_{i}\}\end{eqnarray} ganz enthält und Pi ebenfalls als Randpunkt mit derselben Tangentialebene wie Ei besitzt. Es läßt sich zeigen, daß Ei+1 durch diese Forderungen eindeutig bestimmt ist. Die neue Matrix Bi+1, die das nächste Ellipsoid festlegt, entsteht dabei durch Störung von Bi mit einer Matrix vom Rang 1.

    • Abbildung 1 zum Lexikonartikel Ellipsoidmethoden
    © Springer-Verlag GmbH Deutschland 2017
     Bild vergrößern

    Konstruktion des neuen Ellipsoids

    Das Verfahren wird fortgesetzt, bis man entweder einen Mittelpunkt z ∈ P findet oder garantieren kann, daß P = ∅ ist. Letzteres gelingt durch einen Vergleich des Volumens der Ellipsoide Ei mit einer Abschätzung des Mindestvolumens von P ∩ E0.

    Wesentliche historische Bedeutung kommt den Ellipsoidverfahren deswegen zu, weil sie die ersten Polynomzeitverfahren für die lineare Programmierung im Turingmodell waren. Dabei betrachtet man solche Probleme, die nur aus rationalen Eingabedaten bestehen. Ohne Einschränkung nimmt man hier an, das Ausgangssystem bestehe sogar nur aus ganzzahligen Daten (was nach Multiplikation des Systems mit dem gemeinsamen Hauptnenner aller rationalen Daten erreicht werden kann).

    Nun betrachtet man statt A ⋅ x ≤ b ein System strikter Ungleichungen \begin{eqnarray}A\cdot x\lt b+{2}^{-L}\cdot e,\end{eqnarray} wobei e = (1, …, 1)T ist und L die Bitgröße des Ausgangsproblems bezeichnet. Das neue System ist genau dann lösbar, wenn es das alte war. Diese Beziehung zwischen den beiden Systemen basiert wesentlich auf der Ganzzahligkeit der Eingangsdaten und einer dadurch möglichen Abschätzung (nach oben) von der Bitgröße gewisser Lösungen mittels der Cramerschen Regel. Damit läßt sich aus den Ausgangsdaten zum einen ein geeignetes Startellipsoid E0 mit (P ≠ ∅ ⇒ E0 ∩ P ≠ ∅) finden; zum anderen kann man eine untere Schranke für das Volumen V der Schnittmenge von E0 mit der Lösungsmenge \(\mathop{P}\limits^{\sim }\) von A ⋅ x< b + 2−L · e bestimmen. Man wendet jetzt das Verfahren auf \(\mathop{P}\limits^{\sim }\) an und iteriert solange, bis \begin{eqnarray}\text{vol}({E}_{s})\le {\lambda }^{s}\cdot \text{vol}({E}_{0})\lt V\end{eqnarray} ist (was wegen λ < 1 eintreten muß). In dieser Situation gilt \(\mathop{P}\limits^{\sim }\ne \emptyset\) genau dann, wenn der Mittelpunkt zs von Es in \(\mathop{P}\limits^{\sim }\) liegt. Nach dem entsprechenden Test bricht das Verfahren ab. Die speziellen Werte für E0 und λ beweisen dann die Polynomialität des Verfahrens in Abhängigkeit der Bitgröße der Eingabedaten. Dieser Nachweis der Polynomialität gelang erstmals Khachiyan 1979. Ellipsoidmethoden wurden bereits vorher von Nemirovskiǐ-Yudin und Shor verwendet.

    Trotz seiner Überlegenheit gegenüber der Simplexmethode im worst-case-Verhalten zeigten praktische Versuche, daß die Ellipsoidmethode i. allg. nicht effizienter als die Simplexmethode ist und numerische Instabilitäten zeigt. Dies hat die Suche nach weiteren Verfahren initiiert, die sowohl theoretisch mit polynomialem Aufwand (im Turingmodell) arbeiten, als auch praktisch schnell ausführbar sind. Als Ergebnis dieser Suche stehen heute innerePunkte Methoden im Zentrum des Interesses.

    Abschließend sei bemerkt, daß es keine Funktion nur in der geometrischen Dimension n · m eines linearen Optimierungsproblems {x|A · x ≤ b, A ∈ ℝm×n} gibt, die die Anzahl der arithmetischen Operation der bekannten Ellipsoidmethoden nach oben beschränkt. Ellipsoidverfahren sind daher nicht polynomial in algebraischen Rechenmodellen (Ergebnis von Traub und Wozniakowski (1982)).

    [1] Grötschel, M.; Lovasz, L.; Schrijver, A.: Geometrie Algorithms and combinatorial optimization. Springer-Verlag Heidelberg, 1988.
    [2] Khachiyan, L.G.: A polynomial algorithm in linear programming. Soviet Mathematics Doklady 20, 1979.

    Copyright Springer Verlag GmbH Deutschland 2017
    • Die Autoren
    - Prof. Dr. Guido Walz

    Schreiben Sie uns!

    Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.

    Artikel zum Thema

    Themenkanäle

    Partnerinhalte

    Bitte erlauben Sie Javascript, um die volle Funktionalität von Spektrum.de zu erhalten.