Eine endliche Inzidenzstruktur ist ein Tripel \(({\mathscr{P}},{\mathscr{B}},I)\), wobei

• \({\mathscr{P}}\) eine endliche Menge ist, deren Elemente Punkte genannt werden,

• \({\mathscr{B}}\) eine endliche Menge ist, deren Elemente Blöcke genannt werden,

• \(I\subseteq {\mathscr{P}}\times {\mathscr{B}}\) eine Relation ist, die sog. Inzidenzrelation.

Ist (P, B) ∈ I, so sagt man, der Punkt P ist mit dem BlockB inzident. Man kannden Block \(B\in {\mathscr{B}}\) auch mit der Punktmenge \({\mathscr{P}}\) die Menge der Mädchen, und sei \({\mathscr{B}}\) die Menge der Dreierreihen, die im Laufe der Woche vorkommen. Die Inzidenz wird so definiert, daß der „Punkt“ \(P\in {\mathscr{P}}\) genau dann auf dem „Block“ \(B\in {\mathscr{B}}\) liegt, wenn das Mädchen P in der Reihe B ist. Dann hat die Inzidenzstruktur \(({\mathscr{P}},{\mathscr{B}},I)\) folgende Eigenschaften:

• Es gibt genau v = 15 Punkte.
• Jeder Block enthält genau k = 3 Punkte.
• Je zwei Punkte sind in genau einem Block enthalten.
• Es gibt einen Parallelismus von \({\mathscr{B}}\), d. h. eine Partition \({\mathscr{B}}={\cup }_{i}{{\mathscr{B}}}_{i}\) der Menge der Blöcke, so daß jedes \({{\mathscr{B}}}_{i}\) eine Partition der Menge der Punkte ist. (\({{\mathscr{B}}}_{i}\) entspricht den Reihen des i-ten Tages.)

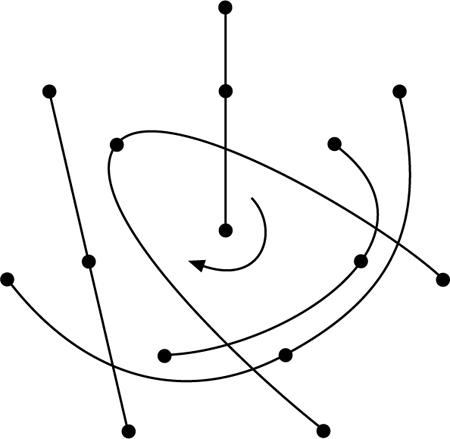
Dies besagt, daß \(({\mathscr{P}},{\mathscr{B}},I)\) ein auflösbarer Blockplan mit Parametern 2-(15,3,1) ist. Das Kirkmansche Schulmädchenproblem ist also ein Problem der endlichen Geometrie, das lautet: Gibt es einen auflösbaren 2-(15,3,1)-Blockplan? Die Antwort lautet: Ja (siehe Abbildung; die anderen Tage erhält man durch Rotation um den Mittelpukt).

Mit diesem Problem ist auch ein zentrales Gebiet der endlichen Geometrie angesprochen: die Theorie der Blockpläne (Designs). Eine elementare Einführung in dieses Gebiet bietet [3]; ein Standardwerk ist [2].

Ein anderes klassisches Problem ist das Eulersche Problem der 36 Offiziere: Aus sechs Regimentern werden je sechs Offiziere derart ausgewählt, daß jeder von sechs Dienstgraden vertreten ist. Diese 36 Offiziere sollen nun derart in einem Quadrat aufgestellt werden, daß in jeder Reihe und in jeder Spalte (=Kolonne) jeder Dienstgrad und jedes Regiment genau einmal vertreten ist. Ist dies möglich?

Bei diesem Problem geht es darum, zwei orthogonale lateinische Quadrate der Ordnung 6 zu finden. Man kann es aber auch folgendermaßen umformulieren: Sei \({\mathscr{P}}\) die Menge der 36 Positionen im Quadrat, in dem die Offiziere aufgestellt werden. Die Menge \({\mathscr{B}}\) setzt sich aus vier Arten von Blöcken zusammen, die alle jeweils sechs Elemente haben: \({{\mathscr{B}}}_{1}\) enthält als Blöcke die sechs Zeilen des Quadrates. \({{\mathscr{B}}}_{2}\) enthält als Blöcke die sechs Spalten des Quadrates. \({{\mathscr{B}}}_{3}\) enthält sechs Blöcke, die jeweils den Offizieren eines Regimentes entsprechen. \({{\mathscr{B}}}_{4}\) enthält sechs Blöcke, die jeweils den Offizieren eines Dienstgrades entsprechen. Zusammen ergibt dies eine Inzidenzstruktur mit folgenden Eigenschaften:

• Durch je zwei Punkte geht höchstens ein Block.
• Ist B ein Block und P ein Punkt, der nicht in B enthalten ist, dann gibt es genau einen Block durch P, der mit B keinen Punkt gemeinsam hat.
• Jeder Block enthält genau sechs Punkte. Jeder Punkt liegt auf vier Geraden.

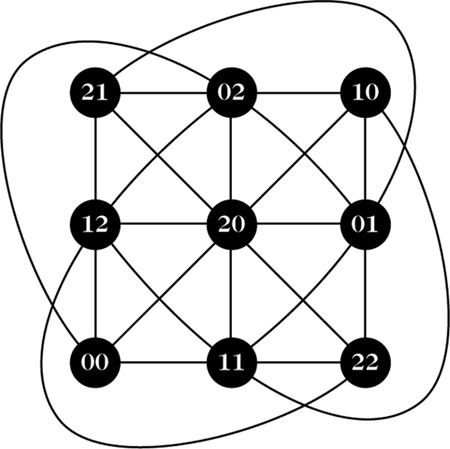
Eine geometrische Struktur mit den ersten beiden Eigenschaften ist ein Netz. Man kann zeigen, daß es kein Netz gibt, das auch die dritte Eigenschaft hat. Wenn man dagegen nur drei Punkte pro Block haben will (was drei Regimentern und drei Dienstgraden entspricht), dann existiert ein solches Netz – die affine Ebene der Ordnung 3.

Sind die Mengen der Punkte und Geraden endlich, so spricht man von einer endlichen projektiven Ebene bzw. einem endlichen projektiven Raum.

Man kann endliche projektive Räume folgendermaßen konstruieren: sei n ≥ 3, und sei V ein n-dimensionaler Vektorraum über einem endlichen Körper K. Sei \({\mathcal{P}}\) die Menge der eindimensionalen Unterräume von V, und sei \({\mathcal{L}}\) die Menge der zweidimensionalen Unterräume von V. Ein Punkt \(P\in {\mathcal{P}}\) sei mit einer Geraden \(l\in {\mathcal{L}}\) inzident, wenn \(P\subset l\) gilt. Dann ist (\({\mathcal{P}}\), \({\mathcal{L}}\), I) ein endlicher projektiver Raum. Falls n = 3 ist, so handelt es sich um eine projektive Ebene. Jeder endliche projektive Raum, der keine projektive Ebene ist, geht auf diese Konstruktion zurück.

Jede Gerade eines endlichen projektiven Raumes enthält die gleiche Anzahl q + 1 von Punkten. Die Zahl q heißt Ordnung des projektiven Raumes. Obige Konstruktion liefert projektive Räume für alle Ordnungen q, die Potenzen von Primzahlen sind. Ein zentrales Problem der endlichen Geometrie ist die Frage, ob es eine endliche projektive Ebene gibt, deren Ordnung keine Potenz einer Primzahl ist. Der Satz von Bruck und Ryser lautet:

Ist q ≡ 1 oder 2 (mod 4), und ist q nicht die Summe zweier Quadratzahlen, so gibt es keine projektive Ebene der Ordnung q.

Ferner ist bekannt, daß keine projektive Ebene der Ordnung 10 existiert. Alle anderen Fälle sind offen.

In endlichen projektiven Räumen gibt es viele interessante Strukturen. Zentrale Bedeutung haben die Quadriken, die die wichtigsten Beispiele der Polarräume sind. Weitere Untersuchungsgegenstände sind z. B. Bögen, Kappen, Unitale, blockierende Mengen und Faserungen.

Anwendungen der endlichen projektiven Geometrie gibt es u. a. in der Codierungstheorie und der Kryptologie. Eine elementare Einführung findet sich in [4]. Ein grundlegendes Werk über projektive Ebenen ist [11]. Ein umfassendes Werk über projektive Geometrie über endlichen Körpern bilden die Bände [8], [9], [10].

Eine gemeinsame Verallgemeinerung von projektiven Räumen und Polarräumen sind Gebäude. Die Theorie der Gebäude wurde von Jacques Tits [12] entwickelt, um den einfachen Lie-Gruppen, später den Chevalley-Gruppen, eine geometrische Interpretation zu geben. Es handelt sich um Geometrien, auf denen diese Gruppen als Automorphismengruppen operieren. Die Theorie der Gebäude stellt einen Verbindungspunkt zwischen der endlichen Geometrie und der Gruppentheorie dar. Eine Einführung in die Theorie der Gebäude findet sich in [5] und in [6].

Eine weitere Verallgemeinerung stellt die Diagrammgeometrie dar. Diese dient der allgemeinen Untersuchung geometrischer Strukturen, die sich aus mehr als zwei Arten von Objekten (etwa Punkten, Geraden und Ebenen) zusammensetzen. Auch hier spielen gruppentheoretische Aspekte eine zentrale Rolle.

Eine Zusammenstellung der wichtigsten Gebiete der endlichen Geometrie findet sich in [6].