eine Methode, alle Primzahlen unterhalb einer gegebenen Schranke N zu finden.

Man schreibt zunächst die natürlichen Zahlen von 2 bis N auf. Von diesen markiert (oder streicht) man alle Vielfachen von 2, die größer als 2 sind. Sodann markiert man alle Vielfachen von 3, die größer als 3 sind. Anschließend sucht man die nächste nichtmarkierte Zahl, das ist jetzt 5, und markiert alle Vielfachen davon, die größer als 5 sind. So fährt man fort, indem man bei jedem Schritt die nächstgrößere nichtmarkierte Zahl p sucht, und alle Vielfachen von p, die größer als p sind, markiert. Ist die nächstgrößere nichtmarkierte Zahl \(p\gt \sqrt{N}\), so kann man aufhören, denn alle Vielfachen kp mit \begin{eqnarray}p\lt kp\le N\end{eqnarray} waren bereits in den vorangegangenen Schritten markiert worden.

Die am Ende übrig gebliebenen (nichtmarkierten) Zahlen sind genau die Primzahlen p ≤ N.

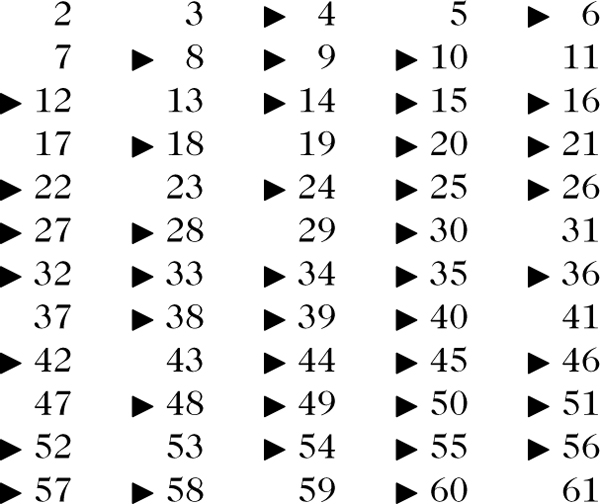
Wir illustrieren das Verfahren für N = 61. Man erhält:

Die Primzahlen bis 61 sind also 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61. Übrigens folgt aus dem Dirichletschen Primzahlsatz, daß jede der Spalten in obiger Liste – außer der vorletzten – unendlich viele Primzahlen enthält!

Diese Methode läßt sich recht einfach auf einem Computer programmieren, sie ist für große Werte von N jedoch nicht sehr effizient. Durch einige kleinere Tricks (z. B. indem man sich von vorne herein auf Restklassen ±1 mod 6 beschränkt) kann man den Algorithmus ein bißchen effizienter machen.

Will man jedoch große Primzahlen konstruieren, wie sie etwa beim RSA-Verfahren zur Codierung benötigt werden, so ist es sinnvoller, auf andere Primzahltests zurückzugreifen.