Lexikon der Mathematik: Euler-Poincarésche Formel
stellt eine Beziehung zwischen dem Geschlecht einer Fläche und der Ordnung n, Kantenzahl m und der Anzahl l der Länder einer kreuzungsfreien Einbettung eines GraphenG in diese Fläche her, für die alle Länder homöomorph zur Ebene ℝ2 sind. Eine solche Einbettung nennt man 2-Zellen Einbettung.
Die Länder einer kreuzungsfreien Einbettung eines Graphen in eine orientierbare oder nichtorientierbare Fläche beliebigen Geschlechts werden dabei analog zu den Ländern eines ebenen Graphen definiert.
Für die orientierbare Fläche Sh vom Geschlecht h gilt nach der Euler-Poincaréschen Formel unter den gegebenen Voraussetzungen
Im speziellen Fall einer Einbettung in die Kugel, d. h. die orientierbare Fläche S0 vom Geschlecht Null, heißt die Euler-Poincarésche Formel auch Eulersche Polyederformel und wurde bereits 1750 von L. Euler für die Ecken, Kanten und Seitenflächen eines konvexen Polyeders bewiesen.
Eine einfache und nützliche Folgerung aus der Euler-Poincaréschen Formel ist die Aussage, daß jeder planare Graph mit Taillenweite g und der Ordnung n höchstens
Insbesondere besitzt jeder planare Graph der Ordnung n also höchstens 3n − 6 Kanten.
Weiterhin kann man schließen, daß es in jedem planaren Graphen mindestens eine Ecke vom Grad kleiner oder gleich fünf gibt.
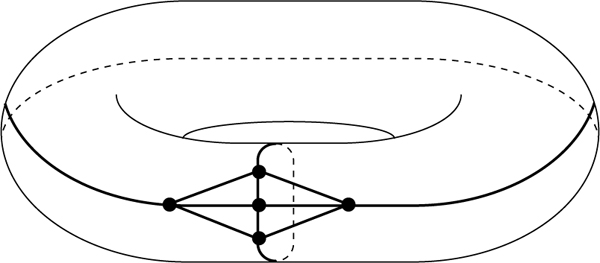
Eine 2-Zellen Einbettung des vollständigen Graphen K5 mit 5 Ecken, 10 Kanten und 5 Ländern in den Torus (Geschlecht 1). Die Euler-Poincarésche Formel liefert 5 − 10 + 5 = 2 − 2 · 1.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.