L. Volkmann

Ein Graph (oder auch Pseudograph) G, der einen geschlossenen Kantenzug W besitzt, welcher alle Kanten des Graphen enthält, für den also K(W) = K(G) gilt, heißt Eulerscher Graph, und W wird dann Eulersche Tour genannt. Ein (nicht notwendig geschlossener) Kantenzug W von G mit K(W) = K(G) heißt Eulerscher Kantenzug.

Angeregt durch das bekannte Königsberger Brückenproblem (Graphentheorie) hat L.Euler 1736 folgende verblüffend einfache Charakterisierung der nach ihm benannten Graphen entdeckt.

Ein zusammenhängender Graph ist genau dann Eulersch, wenn jede Ecke geraden Grad hat.

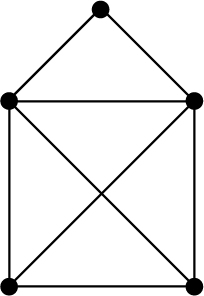
Da der erste vollständige Beweis dieser Charakterisierung erst 1873 von C.Hierholzer gegeben wurde, wird er auch Satz von Euler-Hierholzer genannt. Aus diesem Satz ergibt sich leicht, daß ein zusammenhängender Graph genau dann einen Eulerschen Kantenzug besitzt, wenn er zwei Ecken oder keine Ecke ungeraden Grades hat. Im Fall, daß der Graph genau zwei Ecken ungeraden Grades aufweist, muß der Eulersche Kantenzug in einer dieser Ecken beginnen und in der anderen enden. Diese Folgerung zeigt nun unmittelbar, daß es in dem Multigraphen KBP des Königsberger Brückenproblems keinen Eulerschen Kantenzug geben kann, da alle seine vier Ecken von ungeradem Grad sind. Jedoch, der weltweit bekannteste aller Graphen, der skizzierte Graph HVN mit fünf Ecken, das sogenannte „Haus vom Nikolaus“, besitzt, wie jedes Kind weiß, einen Eulerschen Kantenzug.

Der oben erwähnte Beweis von Hierholzer führt zu einem nach ihm benannten Algorithmus der Komplexität O(|K(G)|), der in einem Eulerschen Graphen G eine Eulersche Tour liefert. Ist G ein Eulerscher Graph, so verläuft der Algorithmus von Hierholzer wie folgt.

Man wähle eine beliebige Ecke x₁ des Graphen und konstruiere von x₁ ausgehend einen beliebigen Kantenzug Z₁ von G, den man nicht mehr fortsetzen kann. Da nach dem Satz von Euler-Hierholzer jede Ecke geraden Grad hat, endet Z₁ notwendig in der Ecke x₁. Ist Z₁ noch keine Eulersche Tour von G, so betrachte man den Faktor \begin{eqnarray}{G}_{1}=G-K({Z}_{1})\end{eqnarray}

und wähle eine Ecke x₂ ∈ E(Z₁), die mit einer Kante von G₁ inzidiert. Von x₂ ausgehend konstruiere man einen beliebigen Kantenzug Z₂ in G₁, den man nicht mehr fortsetzen kann.

Da Z₂ in x₂ endet, kann man Z₁ und Z₂ zu einem geschlossenen Kantenzug von G wie folgt zusammensetzen. Man beginne in x₁, laufe entlang Z₁ bis x₂, durchlaufe nun ganz Z₂ bis x₂, und durchlaufe danach die verbliebenen Kanten von Z₁ bis x₁. Durch Fortsetzung dieses Verfahrens erhält man nach endlich vielen Schritten schließlich eine Eulersche Tour des Graphen G.

Die nächste interessante notwendige und hinreichende Bedingung für Eulersche Graphen wurde 1912 von O.Veblen gegeben.

Ein zusammenhängender Graph ist genau dann Eulersch, wenn er sich als Vereinigung von kantendisjunkten Kreisen darstellen läßt.

Ausgehend von diesem Ergebnis bewiesen J.A. Bondy und F.Y. Halberstam 1986, daß ein zusammenhängender Graph genau dann Eulersch ist, wenn die Anzahl solcher Kreiszerlegungen ungerade ist.

Man nennt eine Familie von nicht notwendig verschiedenen Kreisen in einem beliebigen Graphen H eine doppelte Kreisüberdeckung von H, wenn jede Kante von H zu genau zwei dieser Kreise gehört. Nach dem Satz von Veblen hat jeder Eulersche Graph natürlich eine doppelte Kreisüberdeckung. Eine bis heute ungelöste Vermutung von G.Szekeres aus dem Jahre 1973, die sogenannte „cycle-double-cover“-Vermutung, besagt, daß jeder Graph ohne Brücken eine doppelte Kreisüberdeckung besitzt.

Eine weitere neuere Charakterisierung der Eulerschen Graphen geht auf S.Toida (1973) und T.A.McKee (1984) zurück. Ein zusammenhängender Graph ist genau dann Eulersch, wenn jede Kante des Graphen zu einer ungeraden Anzahl von Kreisen gehört.

Eng verbunden mit den Eulerschen Graphen ist das äußerst wichtige „chinesischer Postmann-Problem“, kurz CP-Problem, das darin besteht, daß z. B. ein Postbote nach der kürzesten Route in seinem Zustellbereich sucht. Graphentheoretisch kann dieses Problem wie folgt formuliert werden. In einem zusammenhängenden bewerteten GraphenG mit positiver Bewertung ϱ(k) ≥ 0 für alle k ∈ K(G) wird eine geschlossene Kantenfolge W von minimaler Gesamtlänge mit K(W) = K(G) gesucht. Eine solche Kantenfolge nennen wir optimal. Der Name dieses Problems weist auf den chinesischen Mathematiker M.-K.Kwan hin, der 1962 die erste Arbeit zu diesem Problem veröffentlicht hat. Wenn G ein Eulerscher Graph ist, dann liefert jede Eulersche Tour eine optimale Lösung. Ist der Graph G jedoch nicht Eulersch, so müssen einige Kanten zweimal durchlaufen werden. Aber welche? Im Jahre 1973 haben J. Edmonds und E.L. Johnson ganz überraschend einen polynomialen Algorithmus zur Lösung des CP-Problems entdeckt, bei dem sie etwa wie folgt vorgegangen sind.

Es sei U die Menge der Ecken ungeraden Grades von G. Da |U| nach dem Handschlaglemma gerade ist, setzen wir im folgenden |U|= 2p.

1. Für alle Paare u, v ∈ U berechne man (z. B. mit den Algorithmen von Dijkstra oder Floyd-Warshall) die Länge d_ϱ(u, v) eines kürzesten Weges von u nach v in G.

2. Man betrachte den vollständigen bewerteten Graphen K_2p mit der Eckenmenge U und der Bewertung σ (uv) = d_ϱ(u, v). In diesem vollständigen Graphen bestimme man dann ein perfektes Matching M ={u₁v₁, u₂v₂,…, u_pv_p} von minimaler Bewertung. Man kann ein solches Matching mit der Komplexität O(p³) berechnen. Allerdings würde die Beschreibung dieses schwierigen Verfahrens die Grenzen des vorliegenden Lexikons überschreiten, und daher sei der Leser z. B. auf das ausführliche Lehrbuch [3] verwiesen.

3. Verdoppelt man nun in G die Kanten der kürzesten Wege von u_i nach v_i (mit gleicher Bewertung) für i = 1, 2,…, p, so entsteht ein bewerteter Eulerscher Multigraph G^∗, dessen Eulersche Tour eine optimale Kantenfolge in G induziert (Verdopplung von Kanten bedeutet für den Briefträger, daß er diese Kanten (Straßen) zweimal durchlaufen muß).

Vertiefte Informationen zur Theorie der Eulerschen Graphen findet man in den umfassenden Monographien von H.Fleischner [1], [2].

[2] Fleischner, H.: Eulerian Graphs and Related Topics, Part 1, Vol 2. Ann. Discrete Math. 50, North-Holland Amsterdam, 1991.

[3] Lovász, L.; Plummer, M.D.: Matching Theory. Ann. Discrete Math. 29, North-Holland Amsterdam, 1986.