der geometrische Ort der Krümmungsmittelpunkte einer ebenen Kurve α(s).

Eine parametrische Gleichung der Evolute ist die folgende: Es sei α(s) = (ξ(s), η(s)), s der Bogenlängenparameter von α, und κ(s) ihre Krümmung. Dann hat die Evolute die parametrische Gleichung \begin{eqnarray}\xi^* (s)=\xi (s)-\frac{{n}{^{\prime\prime} }(s)}{\kappa (s)},\,\,\eta^*(s)=\eta (s)+\frac{{\xi }{^{\prime\prime} }(s)}{\kappa (s)}.\end{eqnarray}

Eine gleichwertige Charakterisierung gibt der folgende Satz:

Die Evolute einer Kurve ist dieEinhüllende der Schar aller ihrer Normalen.

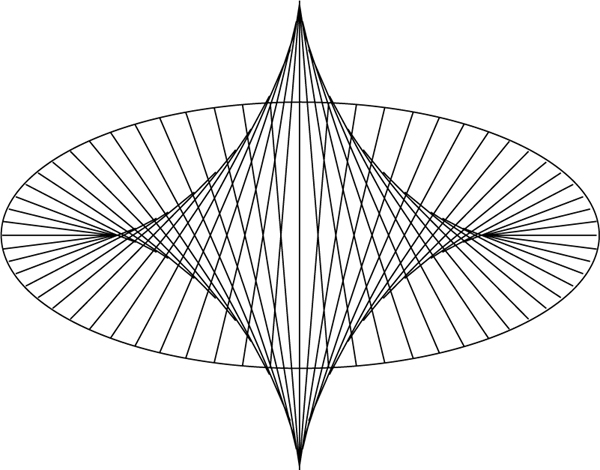
Als Beispiel geben wir die Evolute einer Ellipse mit den Halbachsen a und b; sie hat die Parametergleichung \begin{eqnarray}\begin{array}{ccc}\xi^* (t) & = & \displaystyle \frac{({a}^{2}-{b}^{2})\,{\cos }^{3}t}{a},\\ \eta^* (t) & = & \displaystyle \frac{({a}^{2}-{b}^{2})\,{\sin }^{3}t}{b}\end{array}\end{eqnarray}

und stellt eine Astroide dar, die in Richtung der Koordinatenachsen um die Faktoren a bzw. b gestaucht worden ist.

Die beiden Operationen, die einer ebenen Kurve die Evolute bzw. die Evolvente zuordnen, stehen zueinander in einem ähnlichen Verhältnis wie Differentiation und Integration reeller Funktionen:

Die Evolute der Evolvente einer ebenen Kurve α ist wieder α. Für die umgekehrte Reihenfolge gilt: Bei geeigneter Wahl eines Anfangspunktes (Evolvente) stimmt die Evolvente der Evolute von α mit α überein.