Extremalwert, Extremwert, Maximum oder Minimum einer reellwertigen Funktion.

Es sei f eine auf einer beliebigen Menge D (oft D ⊂ ℝⁿ, speziell D ⊂ ℝ ) definierte reellwertige Funktion: Für a ∈ D heißt f(a) Maximum, genauer globales Maximum (oder auch absolutes Maximum) genau dann, wenn f(x) ≤ f(a) für alle x ∈ D gilt. Andere Sprechweisen dafür sind: f hat in a ein globales Maximum oder f nimmt an der Stelle a ein globales Maximum (mit Wert f(a)) an.

Entsprechend sind die Begriffe Minimum, globales Minimum, absolutes Minimum und damit dann (globale oder absolute) Extremwerte definiert. Statt Zielbereich ℝ können allgemeiner Funktionen mit Werten in einer Menge mit geeigneter Ordnungsstruktur betrachtet werden.

Neben der Frage nach absoluten Extremwerten ist auch die Frage nach lokalen – Vergleich nur in einer geeigneten Umgebung von a – und die Betrachtung von Extrema unter Nebenbedingungen wichtig.

Anstelle von Minimum und Maximum sagt man gelegentlich auch Tiefpunkt bzw. Hochpunkt, statt von lokalen spricht man auch von relativen Extremwerten.

Die Suche nach Extremwerten hat von der Fragestellung her zunächst nichts mit Ableitungen zu tun. Wer sucht denn schon das schnellste Auto oder den leckersten Nachtisch über Differentiation! Doch wenn die zu untersuchende Funktion – bei geeignetem D – differenzierbar ist, liefern die Nullstellen der Ableitung Kandidaten für lokale Extrema und damit auch für globale.

Drei Beispiele dazu:

• Die Funktion f(x) :=|x| (x ∈ ℝ) hat im Punkt 0 offenbar ein absolutes Minimum mit Wert 0; denn alle anderen Funktionswerte sind größer als 0. f ist jedoch in 0 nicht differenzierbar!
• Die Ableitung der Funktion f(x) := x³ (x ∈ ℝ) ist 0 im Punkte 0. Die Funktion f hat jedoch in 0 kein Extremum (nicht relativ und erst recht nicht absolut), denn sie ist auf ganz ℝ streng isoton.
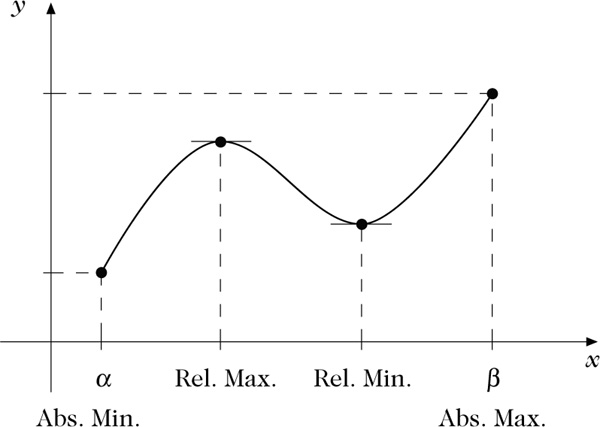
• Die Funktion der nachfolgenden Abbildung hat relative Extrema im „Innern“ des Bereichs – mit waagerechter Tangente, also über Nullstellen der Ableitung auffindbar. Die absoluten Extremwerte liegen jedoch am „Rande“.