Lexikon der Mathematik: F-Verteilung
Fisher-Verteilung, Verteilung aus der Gruppe der theoretisch hergeleiteten Verteilungen für Stichprobenfunktionen.
Die F-Verteilung, gelegentlich auch Fishersche F-Verteilung oder Snedecor-Verteilung genannt, ist das für n1, n2 ∈ ℕ durch die Wahrscheinlichkeitsdichte
\begin{eqnarray}{{f}_{{{n}_{1}},{{n}_{2}}}}:{{\mathbb{R}}^{+}}\backepsilon x\to \frac{{{\left( \frac{{{n}_{1}}}{{{n}_{2}}} \right)}^{\frac{{{n}_{1}}}{2}}}}{B\left( \frac{{{n}_{1}}}{2},\frac{{{n}_{2}}}{2} \right)}\frac{{{x}^{\frac{{{n}_{1}}}{2}-1}}}{{{\left( 1+\frac{{{n}_{1}}}{{{n}_{2}}}x \right)}^{\frac{{{n}_{1}}+{{n}_{2}}}{2}}}}\in {{\mathbb{R}}^{+}}\end{eqnarray}
\begin{eqnarray}B\left( p,q \right):=\underset{0}{\overset{1}{\mathop \int }}\,{{t}^{p-1}}{{\left( 1-t \right)}^{q-1}}dt\end{eqnarray}
definierte Wahrscheinlichkeitsmaß.Noch genauer heißt diese Verteilung F-Verteilung mit n1, n2 Freiheitsgraden und wird mit \({{F}_{{{n}_{1}},{{n}_{2}}}}\) bezeichnet. Für x gegen Unendlich strebt \({{f}_{{{n}_{1}},{{n}_{2}}}}\) gegen Null. Für n1 > 2 gilt dies auch für x gegen Null. In diesem Fall besitzt \({{f}_{{{n}_{1}},{{n}_{2}}}}\) einen eindeutig bestimmten Modalwert an der Stelle
\begin{eqnarray}x=\frac{{{n}_{2}}\left( {{n}_{1}}-2 \right)}{{{n}_{1}}\left( {{n}_{2}}+2 \right)}.\end{eqnarray}
Für n1 = 2 existiert ein Modalwert an der Stelle x = 0 und für n1 = 1 strebt \({{f}_{{{n}_{1}},{{n}_{2}}}}\) für x gegen Null gegen Unendlich. Die Freiheitsgrade bestimmen die Gestalt der nicht symmetrischen Dichtefunktion.
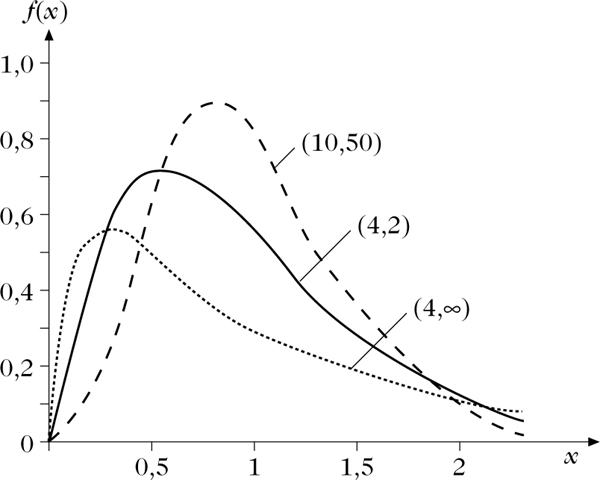
Dichtefunktion der F-Verteilung für die Freiheitsgrade (n1, n2) = (4, ∞), (4, 2), (10, 50)
Eine Zufallsvariable X besitzt genau dann eine \({{F}_{{{n}_{1}},{{n}_{2}}}}\)-Verteilung, wenn sie wie der Quotient \(\frac{{{X}_{1}}/{{n}_{1}}}{{{X}_{2}}/{{n}_{2}}}\) verteilt ist, in dem X1 und X2 zwei unabhängige Zufallsvariablen bezeichnen, von denen X1 eine χ2-Verteilung mit n1 und X2 eine χ2-Verteilung mit n2 Freiheitsgraden besitzt.
Für n2 ≤ 2 besitzt die \({{F}_{{{n}_{1}},{{n}_{2}}}}\)-verteilte Zufallsvariable X keinen endlichen Erwartungswert und für n2 ≤ 4 keine endliche Varianz. Ansonsten gilt
\begin{eqnarray}E\left( X \right)=\frac{{{n}_{2}}}{{{n}_{2}}-2}\end{eqnarray}
und\begin{eqnarray}Var\left( X \right)=\frac{2n_{2}^{2}\left( {{n}_{1}}+{{n}_{2}}-2 \right)}{{{n}_{1}}{{\left( {{n}_{2}}-2 \right)}^{2}}\left( {{n}_{2}}-4 \right)}.\end{eqnarray}
<?PageNum _226Die F-Verteilung ist von großer Bedeutung für die Statistik. In der Praxis wird nur mit den Quantilen der F-Verteilung gearbeitet, die tabelliert vorliegen. Für die Benutzung dieser Tabellen ist folgende Beziehung zu beachten, die unmittelbar aus der Definition der F-Verteilung folgt:
\begin{eqnarray}X\tilde{\ }{{F}_{{{n}_{1}},{{n}_{2}}}}\,\text{genau}\,\text{dann,}\,\text{wenn}\,\frac{1}{X}\tilde{\ }{{F}_{{{n}_{2}},{{n}_{1}}}}.\end{eqnarray}
\begin{eqnarray}{{F}_{{{n}_{1}},{{n}_{2}}}}\left( \alpha \right)=\frac{1}{{{F}_{{{n}_{2,}}{{n}_{1}}}}\left( 1-\alpha \right)}.\end{eqnarray}
Seien \(S_{1}^{2}\) und \(S_{2}^{2}\) die Stichprobenvarianzen (empirische Streuungen) zweier unabhängiger Stichproben vom Umfang n1 und n2 aus zwei normalverteilten Grundgesamtheiten mit den Varianzen \(\sigma _{1}^{2}\) und \(\sigma _{2}^{2}\). Man kann zeigen, daß für j = 1, 2 die Zufallsgrößen\begin{eqnarray}\frac{\left( {{n}_{j}}-1 \right)S_{j}^{2}}{\sigma _{j}^{2}}\end{eqnarray}
eine χ2-Verteilung mit (nj −1) Freiheitsgraden besitzen. Daraus folgt, daß die Stichprobenfunktion\begin{eqnarray}F=\frac{S_{1}^{2}/\sigma _{1}^{2}}{S_{2}^{2}/\sigma _{2}^{2}}\end{eqnarray}
eine F-Verteilung mit (n1 — 1) und (n2 − 1) Freiheitsgraden besitzt. Diese Stichprobenfunktion liegt dem F-Test zum Prüfen der Gleichheit zweier Varianzen zugrunde. Unter der Annahme, daß die Hypothese\begin{eqnarray}H:\sigma _{1}^{2}=\sigma _{2}^{2}\end{eqnarray}
F-verteilte Stichprobenfunktionen werden auch in der Regressionsanalyse als Testgrößen zur Bestimmungder Ordnung von Regressionspolynomen mittels Hypothesentests verwendet.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.