Die Faktorenanalyse ist eine Methode zur Analyse von Beziehungen von untereinander abhängigen zufälligen Merkmalen.

Dabei versucht man, diese Merkmale auf gemeinsame wenige Ursachenkomplexe, die sogenannten Faktoren zurückzuführen. Die Methode wurde von Hotelling (1933), Lawley (1940) und Thurstone (1947) im Rahmen der mathematischen Statistik begründet und findet insbesondere in der Psychologie und Soziologie breite Anwendung.

Mathematisch formuliert ist die Faktorenanalyse eine Methode zur Untersuchung der Kovarianzmatrix eines reellen zufälligen Vektors \(\overrightarrow{X}=(X_{1},\ldots,X_{m})\) dessen Komponenten X_i, i = 1, …, m die zufälligen Merkmale beschreiben. Hierbei legt man das folgende Modell zugrunde: \begin{eqnarray}{X}_{i}=\displaystyle \sum _{j=1}^{s}{a}_{ij}{F}_{j}+{\varepsilon }_{i},i=1,\ldots,m(s\le m);\end{eqnarray}

<?PageNum _121X_i – sind die vorher standardisierten zufälligen Merkmale, d. h., es gilt EX_i = 0 und V(X_i) = 1,i = 1, …, m; (diese Standardisierung erreicht man immer durch die lineare Transformation \({X}_{i}:=\frac{{X}_{i}-E{X}_{i}}{\sqrt{V({X}_{i})}}\))

F_j – sind die sogenannten zufälligen Faktoren mit EF_j = 0 und V(F_j) = 1, j = 1, …, s;

a_ij – sind reelle Koeffizienten, die den Einfluß des Faktors F_j auf das Merkmal X_i wiedergeben und als Ladungen bzw. Faktorladungen bezeichnet werden, i = 1, …, m; j = 1, …, s;

ϵ_i – sind untereinander und mit F_j, j = 1, …, s, unkorrelierte Zufallsgrößen mit Eϵ_i = 0 und \(V({\varepsilon }_{i})={\sigma }_{i}^{2}\), i = 1, …, m; diese werden häufig als die durch die s Faktoren nicht erklärbaren Reste bezeichnet.

Für die Kovarianzmatrix \({\Sigma }_{\overrightarrow{X}}=Cov (\overrightarrow{X})\) des Merkmalsvektors \(\overrightarrow{X}\) ergibt sich unter diesen Modell-Annahmen: \begin{eqnarray}\begin{array}{cc}{\Sigma }_{\overrightarrow{X}}:=A{C}_{\overrightarrow{F}}{A}^{T}+{D}_{\overrightarrow{\varepsilon }},\end{array}\end{eqnarray}

wobei \begin{eqnarray}A=\left(\begin{array}{cccc}{a}_{11} & {a}_{12} & \ldots & {a}_{1s}\\ {a}_{21} & {a}_{22} & \ldots & {a}_{2s}\\ \vdots & \vdots & \ddots & \vdots \\ {a}_{m1} & {a}_{m2} & \ldots & {a}_{ms}\end{array}\right)\end{eqnarray}

die Matrix der Faktorladungen, \begin{eqnarray}{D}_{\overrightarrow{\varepsilon }}=\left(\begin{array}{cccc}{\sigma }_{1}^{2} & 0 & \ldots & 0\\ 0 & {\sigma }_{2}^{2} & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & {\sigma }_{m}^{2}\end{array}\right)\end{eqnarray}

die Kovarianzmatrix von \(\overrightarrow{\varepsilon }\), und \begin{eqnarray}{C}_{\overrightarrow{F}}=Cov(\overrightarrow{F})\end{eqnarray}

die Kovarianzmatrix des Vektors der zufälligen Faktoren \(\overrightarrow{F}=({F}_{1},\ldots,{F}_{s})\) sind.

Die Gleichung (1) wird als Hauptgleichung der Faktorenanalyse bezeichnet. Häufig fordert man (aus Gründen der Vereinfachung des Problems), daß die Faktoren unkorreliert sind, daß also \({C}_{\overrightarrow{F}}\) gleich der Einheitsmatrix ist; die Hauptgleichung der Faktorenanalyse lautet dann: \begin{eqnarray}\begin{array}{cc}{\sum }_{\overrightarrow{X}}:=A{A}^{T}+{D}_{\overrightarrow{\varepsilon }}\end{array}\end{eqnarray}

Dies bedeutet, daß die Kovarianzen \({\sigma }_{{X}_{i}{X}_{j}}\) von X_i und X_j und die Varianzen von X_i sich wie folgt beschreiben lassen: \begin{eqnarray}\begin{array}{llll}{\sigma }_{{X}_{i}{X}_{j}} & = & E{X}_{i}{X}_{j} & \\ & = & \displaystyle \sum _{l=1}^{s}{a}_{il}{a}_{jl}\ \mathrm{f}\mathrm{\ddot{u}}\mathrm{r}\ i\ne j\end{array}\end{eqnarray}

und \begin{eqnarray}\begin{array}{cc}1=\displaystyle \sum _{l=1}^{s}{a}_{il}^{2}+{\sigma }_{i}^{2}.\end{array}\end{eqnarray}

Man bezeichnet \begin{eqnarray}{h}_{i}^{2}:=\displaystyle \sum _{l=1}^{s}{a}_{il}^{2}\end{eqnarray}

als Kommunalität von X_i bzgl. der s Faktoren. \({h}_{i}^{2}\) ist der durch die Faktoren erklärte Anteil an der Varianz von X_i. Die Aufgabenstellung der Faktorenanalyse besteht nun darin, eine derartige Zerlegung der Kovarianzmatrix \({\Sigma }_{\overrightarrow{X}}\) zu finden. Da die Matrix \({\Sigma }_{\overrightarrow{X}}\) unbekannt ist wird sie durch die empirische Kovarianzmatrix\begin{eqnarray}{S}_{\overrightarrow{X}}={({s}_{ij})}_{i=1,\ldots,m}^{j=1,\ldots,m},\text{}{s}_{ij}=\frac{1}{n-1}\displaystyle \sum _{k=1}^{n}{x}_{ik}{x}_{jk}\end{eqnarray}

der standardisierten Merkmale X_i ersetzt, die auf der Basis einer konkreten Stichprobe \({\overrightarrow{x}}_{k}=({x}_{1k},\ldots,{x}_{mk})\), k = 1, …, n von \(\overrightarrow{X}\) vom Umfang n berechnet werden. (Im allgemeinen sind die Merkmale X_i nicht von vorneherein standardisiert. In diesem Fall werden die Beobachtungen x_ik von X_i zunächst gemäß der Transformation \begin{eqnarray}{x}_{ik}:=\frac{{x}_{ik}-{\bar{x}}_{i}}{{s}_{i}}\end{eqnarray}

standardisiert, wobei \({\bar{x}}_{i}\) und s_i der empirische Mittelwert und die empirische Streuung der Beobachtungen von X_i sind.)

Die Aufgabe der Faktorenanalyse lautet damit: Finde die Zahl s der Faktoren, A und \({\sigma }_{i}^{2}\) so, daß gilt \begin{eqnarray}\begin{array}{cc}{S}_{\overrightarrow{X}}:=A{A}^{T}+{D}_{\overrightarrow{\varepsilon }},\end{array}\end{eqnarray}

bzw. finde s und A so, daß gilt: \begin{eqnarray}\begin{array}{ccc}{s}_{ij}=\displaystyle \sum _{l=1}^{s}{a}_{il}{a}_{jl} &\ \mathrm{f}\mathrm{\ddot{u}}\mathrm{r}\ i\ne j,i,j=1,\ldots,m.\end{array}\end{eqnarray}

Gemäß (4) ergibt sich dann als Schätzung für \({\sigma }_{i}^{2}\) : \begin{eqnarray}\begin{array}{ccc}{\sigma }_{i}^{2}:=1-{h}_{i}^{2} & \text{mit} & {h}_{i}^{2}:=\displaystyle \sum _{l=1}^{s}{a}_{il}^{2}.\end{array}\end{eqnarray}

Die Aufgabe ist so, wie sie gestellt ist, nicht eindeutig lösbar, auch dann nicht, wenn die Zahl s der Faktoren gegeben ist. Es gibt zur Lösung der Aufgabe verschiedene Verfahren, die unterschiedliche Nebenbedingungen fordern, um die Lösung eindeutig zu machen.

Die am häufigsten verwendeten Methoden der Faktorenanalyse sind die Maximum-Likelihood-Methode, die Hauptkomponentenmethode und die Zentroidmethode.

Bei dem durch Lawley und Maxwell [1] in die Faktorenanalyse eingeführten Maximum-Likelihood-Schätzprinzip <?PageNum _122wird vorausgesetzt, daß sowohl der zufällige Merkmalsvektor \(\overrightarrow{X}\) als auch der Vektor der Reste \(\overrightarrow{\varepsilon }\) einer m-dimensionalen Standardnormalverteilung genügen und voneinander unabhängig sind. Die Anzahl s der Faktoren wird fest vorgegeben. Aufgrund der Kenntnis der Verteilung der Kovarianzmatrix \({S}_{\overrightarrow{X}}\) (Wishart-Verteilung) erhält man für eine mathematische Stichprobe \({\overrightarrow{X}}_{k}=({X}_{1k},\ldots,{X}_{mk})\), k =1, …, n vom Umfang n die folgende Likelihoodfunktion: \begin{eqnarray}\begin{array}{l}L({\sum }_{\overrightarrow{X}};{a}_{ij},{\varepsilon }_{i},i=1,\ldots,m,j=1,\ldots,s)=\\ K|{\sum }_{\overrightarrow{X}}{|}^{-{\scriptstyle \frac{m}{2}}}|{S}_{\overrightarrow{X}}{|}^{{\scriptstyle \frac{n-m-1}{2}}}\exp (-\frac{n}{2}Sp({S}_{\overrightarrow{X}}{\sum }_{\overrightarrow{X}}^{-1})).\end{array}\end{eqnarray}

Dabei sind K eine (nur von m und n abhängige) Konstante, Sp der Spuroperator (Summe der Hauptdiagonalelemente), und |·| bezeichnet die Determinante. Man erhält durch Maximierung der Likelihoodfunktion (Ableitung nach a_ij) und Berücksichtigung der Beziehung (4) folgende Schätzgleichungen: \begin{eqnarray}{A}^{T}({A}^{T}{D}_{\overrightarrow{\varepsilon }}^{-1}A) & = & {A}^{T}{D}_{\overrightarrow{\varepsilon }}^{-1}{S}_{\overrightarrow{X}}-{A}^{T},\end{eqnarray}\begin{eqnarray}{\sigma }_{i}^{2} & = & 1-\displaystyle \sum _{l=1}^{s}{a}_{il}^{2}.\end{eqnarray}

Um die Eindeutigkeit der Schätzungen a_ij und \({\sigma }_{i}^{2}\) zu sichern, fordern Lawley und Maxwell, daß die Matrix \({A}^{T}{D}_{\overrightarrow{\varepsilon }}^{-1}A\) diagonal ist. Die Schätzwerte für a_ij erhält man dann mit geeigneten numerischen Verfahren zur Lösung des nichtlinearen Gleichungssystems (7), (8).

Zur Bestimmung der Anzahl s der Faktoren wird dieses Verfahren in der Regel mehrmals für s = 2, 3,… angewendet. Der Vektor der Faktorladungen \({\overrightarrow{a}}_{j}=({a}_{1j},\ldots,{a}_{mj})\) zu einem neu hinzukommenden Faktor F_j soll dabei wenigstens in zwei Elementen stark von 0 verschieden sein, d. h. der Faktor F_j soll wenigstens zwei Merkmale beeinflussen, andernfalls bricht das Verfahren ab. Ansonsten bricht das Verfahren mit dem kleinsten s ab, ab dem sich die Kommunalitäten nicht mehr wesentlich voneinander unterscheiden, d. h. man wählt die kleinste Anzahl s von Faktoren, durch die die Varianz der Merkmale erklärt werden kann und die wenigstens zwei Merkmale beeinflussen. Unter der obigen Voraussetzung der Normalverteilungen ist auch ein χ²-Test zum Testen der Anzahl s entwickelt worden (siehe auch [1]).

Bei der Hauptkomponentenmethode wird schrittweise ein orthogonales Koordinatensystem von Faktoren konstruiert. Dabei wird in jedem Schritt versucht, die verbliebene Reststreuung maximal auszuschöpfen, d. h. zu verringern. Numerisch führt dieses auf die schrittweise Lösung eines Eigenwertproblems.

Bei der Zentroidmethode handelt es sich eben-falls um ein iteratives, geometrisch motiviertes Extraktionsverfahren der Faktoren auf der Basis der Kovarianzmatrix der Merkmale, dessen Ergebnisse (Ladungen) nicht eindeutig sind. Dabei wird versucht, durch schrittweise Konstruktion eines orthogonalen Koordinatensystems der Faktoren die Kommunalitäten zu maximieren.

Bei der Anwendung der Faktorenanalyse in der Praxis erweist sich häufig die Vorgabe der Anzahl s der Faktoren als auch deren Interpretation als kompliziert. Deshalb wird oft wie oben beschrieben durch schrittweise Erhöhung der Faktorenzahl – dem entspricht eine Änderung des Modells – versucht, interpretierbare Lösungen zu erhalten.

Beispiel. Es ist zu untersuchen, ob sich die Leistung (erreichte Punktzahl X_i, i = 1, …, 5) in den 5 Fächern Mechanik (Me), Analytische Geometrie (AG), Lineare Algebra (LA), Analysis (An) und elementare Statistik (St) auf wenige gemein-same Faktoren zurückführen läßt. Von n = 88 Studenten wurden die jeweils erreichten Punktzahlen bei den 5 Klausuren Me, AG, LA, An und St erfaßt. Auf die Angabe der Datenmatrix x_il, i = 1, …, 5, l = 1, …, 88 sei hier verzichtet. Bei der Durchführung der Faktorenanalyse werden zunächst für jedes Merkmal X_i, i = 1, …, 5 aus den beobachteten Daten x_il, l = 1, …, 88 der empirische Mittelwert \({\overrightarrow{x}}_{i}\) und die empirische Streuung \({s}_{i}^{2}\) des Merkmals berechnet. Anschließend werden alle Beobachtungen gemäß \begin{eqnarray}{x}^{\prime}_{il}:=\frac{{x}_{il}-{\bar{x}}_{i}}{{s}_{i}}\end{eqnarray}

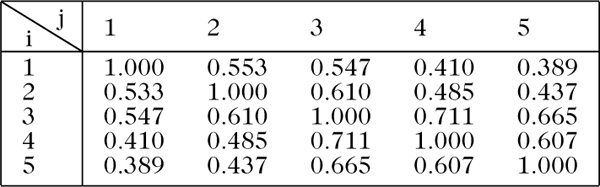
standardisiert und mit den standardisierten Daten die empirische Kovarianzmatrix \({S}_{\overrightarrow{X}}\) berechnet: \begin{eqnarray}{s}_{ij}:=\frac{1}{87}\displaystyle \sum _{l=1}^{88}{x}^{\prime}_{il}{x}^{\prime}_{jl}\end{eqnarray}

In unserem Beispiel erhalten wir als Ergebnis für \({S}_{\overrightarrow{X}}\) die Matrix:

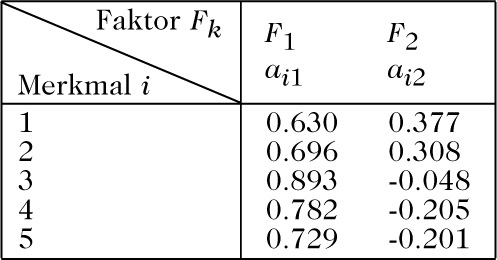
Werden s = 2 Faktoren angesetzt, so ergibt sich als geschätzte Ladungsmatrix nach der Maximum-Likelihood-Methode die in folgender Tabelle angegebene Matrix:

<?PageNum _123

Aus dieser Matrix ergeben sich für die Kummunalitäten der 5 Merkmale: \begin{eqnarray}\begin{array}{c}{h}_{1}^{2}={a}_{11}^{2}+{a}_{12}^{2}={0.630}^{2}+{0.377}^{2}=0.539,\\ {h}_{2}^{2}=0.579,{h}_{3}^{2}=0.800,{h}_{4}^{2}=0.654,{h}_{5}^{2}=0.572.\end{array}\end{eqnarray}

Wir stellen die 5 Merkmale im orthogonalen Koordinatensystem der beiden Faktoren dar; das erste Merkmal (Me) wird dort zum Beispiel durch den Punkt mit den Koordinaten (a₁₁, a₁₂) dargestellt, siehe Abbildung.

Der Ladungsmatrix A in obiger Tabelle sieht man an, daß sich die Ladungen auf die erste Spalte, d. h. den ersten Faktor, konzentrieren. Dies ist ein Hinweis darauf, daß als Ursache für die erreichten Leistungen in den 5 Fächern schon ein Faktor ausreichend wäre. Führt man die Maximum-Likelihoodschätzung mit s = 1 durch, so ergibt sich für den Ladungsvektor \begin{eqnarray}\begin{array}{lll}{\overrightarrow{a}}_{1} & = & ({a}_{11},\ldots,{a}_{51})\\ & = & (0.599,0.668,0.915,0.773,0.724).\end{array}\end{eqnarray}

Die Kommunalitäten für diesen Fall \(({h}_{i}^{2}={a}_{i1}^{2})\) unterscheiden sich (in der Summe) nicht wesentlich vom Fall s = 2. In einem anschließenden χ^2-Test wäre die Vermutung H₀ : s = 1 zu überprüfen.

Literatur

[1] Hartung, J., Elpelt, B.: Multivariate Statistik. R. Oldenbourg Verlag, München Wien 1989.

[2] Jahn, W., Vahle, H.: Die Faktorenanalyse. Verlag Die Wirtschaft, Berlin 1970.

[3] Lawley, D.N., Maxwell, A.E.: Factor Analysis as a Statistical Method. Butterworths, London 1971.

[4] Überla, K.: Faktorenanalyse. Springer-Verlag, Berlin 1968.