Ist G ein Multigraph mit der Eckenmenge E(G), f : E(G) → ℕ₀ eine Abbildung und H ein Faktor von G mit der Eigenschaft d_H(x) = f(x) für alle x ∈ E(G), so nennen wir H einen f-Faktor von G. Im Fall f(x) ≡ k sprechen wir auch von einem k-Faktor.

Es seien H₁, H₂, …, H_r Faktoren von G mit \begin{eqnarray}\begin{array}{l}K(G)=\displaystyle \underset{i=1}{\overset{r}{\cup }}K({H}_{i})\ \ \ \text{und}\\ K({H}_{i})\cap K({H}_{j})=\varnothing\ \ \text{f}\mathrm{\ddot{u}}\text{r}1\ \ \le i\lt j\le r.\end{array}\end{eqnarray}

Dann heißt G faktorisierbar durch die Faktoren H₁, H₂, …, H_r. Sind dabei alle H_i sogar k-Faktoren, so nennt man G auch k-faktorisierbar.

Zum besseren Verständnis der neuen Begriffe geben wir zunächst ein paar einfache Beispiele.

1. Jeder Kreis gerader Länge ist 1-faktorisierbar.
2. Der vollständige Graph K₅ ist 2-faktorisierbar.
3. Ein 3-regulärer Hamiltonscher Graph ist nach dem Handschlaglemma von gerader Ordnung und daher 1-faktorisierbar.

Da jeder 1-Faktor einem perfekten Matching entspricht und umgekehrt, sind die Faktortheorie und die Matchingtheorie eng miteinander verbunden. Einer der ältesten Sätze der Faktortheorie geht auf T.P.Kirkman (1847) und M.Reiß (1859) zurück und spielt eine wichtige Rolle bei der Erstellung von Spielplänen (z. B. Fußballbundesliga).

Jeder vollständige Graph K_2nist 1-faktorisierbar.

Das allgemeine Faktorisierungsproblem wurde jedoch erst von Julius Petersen in Angriff genommen. Petersen publizierte 1891 in der „Acta Mathematica 15“ eine Arbeit mit dem Titel „Die Theorie der regulären graphs“. Diese an Tiefe und Auswirkung bemerkenswerte Abhandlung ist wirklich ein Markstein in der Graphentheorie.

Im Anschluß an ein von P.Gordan und D.Hilbert behandeltes Problem der Invariantentheorie betrachtete Petersen folgende Aufgabe:

Gegeben sei ein homogenes Polynom P in n Veränderlichen x₁, x₂, …, x_n von der Form: \begin{eqnarray}P={({x}_{1}-{x}_{2})}^{{m}_{1,2}}{({x}_{1}-{x}_{3})}^{{m}_{1,3}}\ldots {({x}_{n-1}-{x}_{n})}^{{m}_{n-1,n}}.\end{eqnarray}

Dabei seien m_i,j nicht negative ganze Zahlen, und in jeder der n Veränderlichen sei der Grad von P dieselbe positive Zahl k. Es wird verlangt, P als Produkt von Polynomen derselben Art – aber von kleinerem konstantem Grad in jeder Veränderlichen – darzustellen.

Die fundamentale Idee von Petersen bestand darin, die oben geschilderte Aufgabe in ein graphentheoretisches Problem zu transformieren. Dazu lassen wir nun Petersen selbst zu Wort kommen.

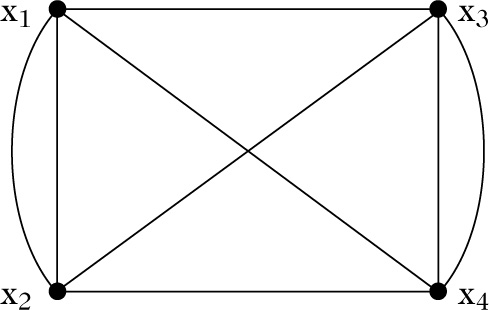
„Man kann der Aufgabe eine geometrische Form geben, indem man x₁, x₂, …, x_n durch beliebige Punkte der Ebene repräsentiert, während der Factor x_m − x_p durch eine beliebige Verbindungslinie zwischen x_m und x_p dargestellt wird. Man erhält so für das Product eine Figur, welche aus n Punkten besteht, die so verbunden sind, dass in jedem Punkte gleich viele Linien zusammenlaufen. Dieselben zwei Punkte können durch mehrere Linien verbunden sein. Als Beispiel betrachte man die Figur I, die das Product \begin{eqnarray}{({x}_{1}-{x}_{2})}^{2}{({x}_{3}-{x}_{4})}^{2}({x}_{1}-{x}_{3})({x}_{2}-{x}_{4})({x}_{1}-{x}_{4})({x}_{2}-{x}_{3})\end{eqnarray}

darstellt.

Englische Verfasser haben für ähnliche Figuren den Namen graph eingeführt; ich werde diesen Namen beibehalten und nenne den graph regulär, weil in jedem Punkte gleich viele Linien zusammenlaufen.

Durch die Ordnung eines graphs werde ich die Anzahl der Punkte (die Ordnung der binären Grundform) verstehen, durch den Grad die Anzahl der in jedem Punkt zusammenlaufenden Linien (den Grad der entsprechenden Invariante). Durch \({G}_{\alpha }^{n}\) oder einfach G_α werde ich einen graph von der Ordnung n und vom Grade α verstehen. Ein solcher lässt sich zerlegen oder in Factoren auflösen, wenn man andere graphs von derselben Ordnung aber niedrigerem Grade finden kann, die durch Überlagerung den gegebenen graph herstellen. Ein graph, der sich nicht in solcher Weise auflösen lässt, heisst primitiv. Unsere Aufgabe geht auf die Bestimmung aller primitiven graphs aus.“

<?PageNum _126

Wir beobachten, daß die von Petersen benutzten Bezeichnungen Graph, Faktor, regulärer Graph, Ordnung eines Graphen und Grad auch heute noch aktuell sind. Außerdem erkennen wir nun deutlich, wie der Name Faktor entstanden ist.

Im Fall regulärer Multigraphen geraden Grades gab Petersen durch seinen I. Satz eine vollständige Lösung des oben gestellten Problems.

Ein Multigraph G ist genau dann 2-faktorisierbar, wenn er 2p-regulär ist.

Einenk-regulärenMultigraphenmitkeinemr-Faktor für 1 ≤ r ≤ k − 1 nennt Petersen primitiv. Aus dem I. Satz von Petersen folgt, daß ein 2p-regulärer Multigraph G genau dann primitiv ist, wenn p = 1 gilt, und G einen Kreis ungerader Länge besitzt.

Die folgenden Beispiele von Petersen zeigen, daß die Situation wesentlich schwieriger wird, wenn man (2p+1)-reguläre Multigraphen betrachtet. Für jedes p ∈ ℕ liefert die folgende Konstruktion einen primitiven (2p + 1)-regulären Multigraphen.

Die Ecke u sei zu 2p + 1 verschiedenen Ecken x₁, x₂, …, x_2p+1 adjazent. Jede Ecke x_i sei mit zwei weiteren Ecken y_i und z_i durch p parallele Kanten verbunden, und schließlich gebe es noch p +1 parallele Kanten zwischen y_i und z_i für i =1, 2, …, 2p + 1.

Da die Ecke u auf keinem Kreis liegt, besitzt dieser (2p + 1)-reguläre Multigraph G keinen 2-Faktor, und daher wegen des I. Satzes von Petersen überhaupt keinen regulären Faktor geraden Grades. Daraus ergibt sich unmittelbar, daß in G auch kein regulärer Faktor ungeraden Grades existiert.

Der Fall p = 1 dieses Beispiels stammt von J.J. Sylvester, mit dem Petersen diese Probleme intensiv diskutiert hat.

Den zweiten Teil seiner Abhandlung widmete Petersen dem Studium der 3-regulären Multigraphen, und er bewies den folgenden fundamentalen Satz.

Ist G ein zusammenhängender 3-regulärer Multigraph mit höchstens zwei Brücken, so besitzt G einen 1-Faktor.

Für p = 1 zeigt das oben angegebene Beispiel, daß dieser II. Satz von Petersen im allgemeinen nicht gilt, wenn man mehr als zwei Brücken zuläßt. Bezugnehmend auf die Ergebnisse von Petersen schrieb D.König 1936 in seinem Buch [1]:

„Diese Abhandlung von Petersen, an der auch Sylvester beteiligt ist, ist sicherlich eine der bedeutendsten Arbeiten über Graphentheorie, scheint aber mehr als 25 Jahre lang fast gänzlich unbeachtet geblieben zu sein.

Es ist nichts darüber bekannt, wie sich der Petersensche Satz auf reguläre Graphen vom Grad 5, 7, 9, … ausdehnen läßt. Petersen hat die Vermutung ausgesprochen, daß auch diese Graphen nur dann primitiv sein können, wenn sie Brücken enthalten.“

Nur zwei Jahre später gab F. Bäbler eine Antwort auf das von König gestellte Problem, und er bewies die Vermutung von Petersen.

Es sei G ein (2p+1)-regulärer undk-fach kantenzusammenhängender Multigraph. Ist t ∈ ℕ₀mit 2t ≤ k, so besitzt G einen 2t-Faktor.

Der große Durchbruch in der Faktortheorie erfolgte dann im Jahre 1947, als W.T. Tutte seine erstaunliche und tiefgreifende notwendige und hinreichende Bedingung für die Existenz eines 1-Faktors vorstellte.

Ein Multigraph G besitzt genau dann einen 1-Faktor, wenn für alle A ⊆ E(G) die Bedingung\begin{eqnarray}q(G-A)\le |A|\end{eqnarray}

erfüllt ist, wobei q(G − A) die Anzahl der Zusammenhangskomponenten ungerader Ordnung in G − A bedeutet.

Aus diesem sogenannten 1-Faktor-Satz lassen sich viele vorher bekannte, aber auch interessante neue Resultate mühelos gewinnen. Das allgemeine f-Faktorproblem wurde fünf Jahre später wiederum von Tutte durch den äußerst schwer zu beweisenden f-Faktor-Satz gelöst.

Es sei G ein Multigraph und f : E(G) → ℕ₀eine Abbildung. Der Multigraph G besitzt genau dann einen f-Faktor, wenn für alle disjunkten Teilmengen X und Y von E(G) gilt:\begin{eqnarray}\displaystyle \sum _{x\in X}f(x)+\displaystyle \sum _{y\in Y}({d}_{G-X}(y)-f(y))-{q}_{G}(X,Y)\ge 0.\end{eqnarray}

Dabei bedeutet q_G(X, Y) die Anzahl der Komponenten U in dem Multigraphen G − (X ∪ Y) mit\begin{eqnarray}{m}_{G}(Y,E(U))+\displaystyle \sum _{u\in E(U)}f(u)\equiv 1\ \text{(mod}\ 2\text{),}\end{eqnarray}

wobei m_G(Y, E(U)) die Anzahl der Kanten von Y nach E(U) in G angibt.

Zwei Jahre vor Tutte, also 1950, hatte H.-B. Belck den f-Faktorsatz schon für konstantes f entdeckt. Als wichtige Erweiterung des f-Faktorsatzes präsentierte L.Lovasz 1970 den sogenannten (g, f)-Faktor-Satz. Sind g, f : E(G) → ℕ₀ zwei Abbildungen mit g(x) ≤ f(x) für alle x ∈ E(G), so heißt ein Faktor H des Multigraphen G ein (g, f)-Faktor, falls \begin{eqnarray}g(x)\le {d}_{H}(x)\le f(x)\end{eqnarray}

für alle x ∈ E(G) erfüllt ist.

Ein Multigraph G besitzt genau dann einen (g, f)-Faktor, wenn für alle disjunkten Teilmengen X und Y von E(G) gilt: \begin{eqnarray}\displaystyle \sum _{x\in X}f(x)+\displaystyle \sum _{y\in Y}({d}_{G-X}(y)-g(y))-{q}_{G}^{* }(X,Y)\ge 0.\end{eqnarray}

<?PageNum _127

Dabei bedeutet \({q}_{G}^{* }\) (X, Y) die Anzahl der Komponenten U in dem Multigraphen G − (X ∪ Y) mit g(x) = f(x) für alle x ∈ E(U) und\begin{eqnarray}{m}_{G}(Y,E(U))+\displaystyle \sum _{u\in E(U)}f(u)\equiv 1\ (\mathrm{mod}\ \text{2}).\end{eqnarray}

Die beiden Sätze von Petersen sowie der Satz von König (1916), daß jeder reguläre bipartite Graph 1-faktorisierbar ist, zählen zu den Keimzellen der Faktor- und Matchingtheorie, die heute zu den am weitesten entwickelten Teilgebieten der Graphentheorie gehören.

Der interessierte Leser sei auf das umfassende Werk von L.Lovász und M.D.Plummer [2] hingewiesen, das eine Fülle von Resultaten zu diesem Thema enthält.

Die wichtigsten Ergebnisse der Faktortheorie bis 1985, die fast ausschließlich auf den Faktorsätzen von Belck, Tutte und Lovász basieren, findet man in dem Übersichtsartikel „Factors and factorizations of graphs – a survey“ von J.Akiyama und M.Kano in „J. Graph Theory 9 (1985)“.

Die Entwicklung der Faktortheorie von den Anfängen bis 1995, mit besonderer Würdigung der Petersenschen Sätze, wurde in der 1995 erschienenen Arbeit „Regular graphs, regular factors, and the impact of Petersen’s Theorems“ von L.Volkmann in den „Jahresber. Deutsch. Math.-Verein. 97“ beschrieben.

Literatur

[1] König, D.: Theorie der endlichen und unendlichen Graphen. Akademische Verlagsgesellschaft M.B.H. Leipzig, 1936.

[2] Lovász, L.; Plummer, M.D.: Matching Theory. Ann. Discrete Math. 29, North-Holland Amsterdam, 1986.

[3] Volkmann, L.: Fundamente der Graphentheorie. Springer Wien New York, 1996.