Lexikon der Mathematik: Frobenius-Morphismus
spezieller Morphismus auf einem Schema.
Für kommutative \(\mathbb{F}_{p}\)-Algebren A (wobei p eine Primzahl und \(\mathbb{F}_{p}\) der Körper mit p Elementen ist) ist die Abbildung a ↦ ap (a ∈ A) ein Ringhomomorphismus. Für jedes Schema X über \(\mathbb{F}_{p}\) erhält man daher einen Morphismus FX : X → X durch die identische Abbildung der zugrundeliegenden Räume und den Komorphismus \(F_{X}^{*}(f)=f^{p}\). Dieser Morphismus heißt der (absolute) Frobenius-Morphismus.
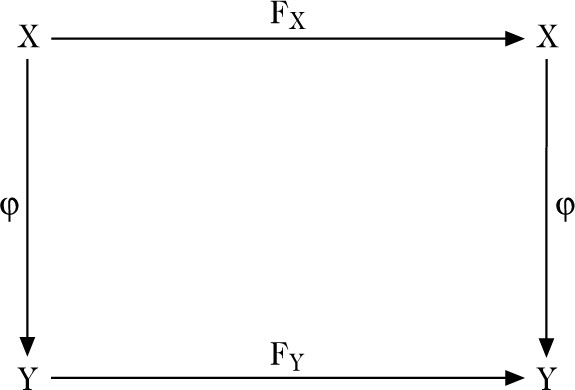
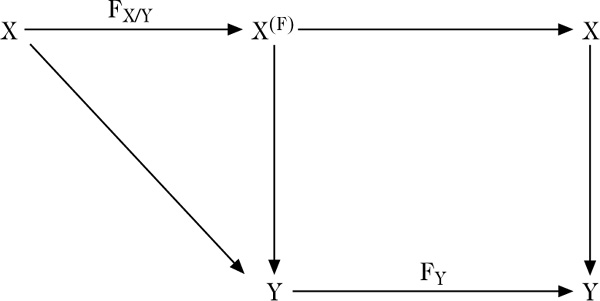
Für jeden Morphismus von \(\mathbb{F}_{p}\)-Schemata, \(X\mathop{\rightarrow}^{\varphi}Y\) erhält man ein kommutatives Diagramm wie in Abbildung 1 dargestellt. Man erhält also eine Zerlegung von FX über das FaserproduktX(F) von FY und φ als Y-Morphismus FX/Y, komponiert mit der in Abbildung 2 dargestellten Projektion. FX/Y heißt (relativer) Frobenius-Morphismus von X über Y. Speziell erhält man für k-Schemata X über einem vollkommenen Körper k eine Zerlegung FX = σ ◦ FX/k mit einem Isomorphismus σ : X(F) → X.
Abbildung 1
Abbildung 2
Ist k ein Körper mit q = pn Elementen, und ist k ⊂ k1 ⊂ K, k1 ein Körper mit qm Elementen, so sind die k1-rationalen Punkte von X die Fixpunkte von \(X\mathop{\to }\limits^{\varphi }Y\), die Anzahl dieser Punkte kann durch globale Invarianten von X ausgedrückt werden.
Wichtige Anwendungen findet der Frobeniusmorphismus auch in der komplexen algebraischen Geometrie. So ist z. B. der Nachweis der Existenz von rationalen Kurven auf Fano-Varietäten nur über den Umweg der Charakteristik p und den Gebrauch des Frobenius-Morphismus möglich.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.