die Erweiterung des Begriffs der Fuzzy-Zahl auf eine Grundmenge ℝⁿ.

Ein scharfer Punkt, d. h. ein Vektor \(\bar{\mathbf{x}}=(\bar{x}_{1},\ldots,\bar{x}_{n})^{T}\), bildet den Kern des Fuzzy-Punktes, von dem aus die Zugehörigkeitsfunktion nach allen Seiten monoton fällt.

Häufig benutzte Beispiele sind

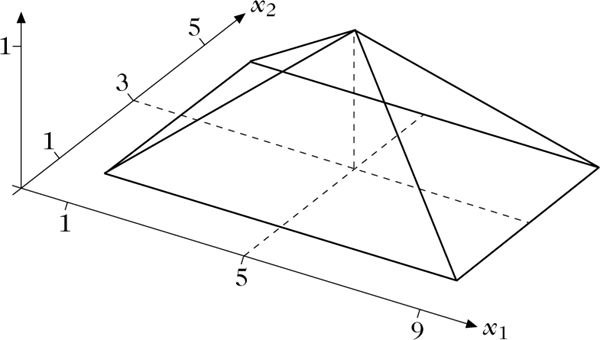
• die Hyperpyramide mit der Zugehörigkeitsfunktion \begin{array}\mu ({x}_{1},\ldots,{x}_{n})=\mu (\bf{x})=\\ \,\,\,\,\,\,=\max \left[0,1-\displaystyle \sum _{j=1}^{n}{c}_{j}\cdot |{x}_{j}-{\bar{x}}_{j}|\right],\end{array} wobei c_j > 0,
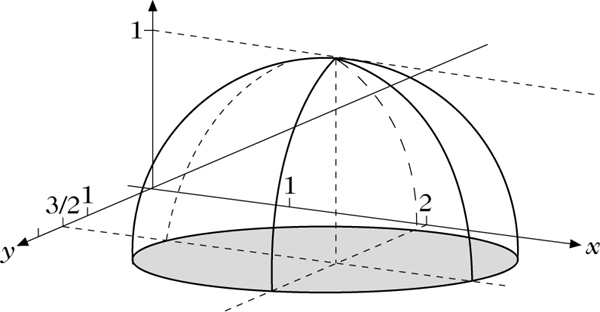
• die Hyperhalbkugel mit der Zugehörigkeitsfunktion \begin{array}\mu ({x}_{1},\ldots,{x}_{n})=\mu (\bf x)=\\ \,\,\,\,\,\,=\max \left[0,\sqrt{1-\displaystyle \sum _{j=1}^{n}{({x}_{j}-{\bar{x}}_{j})}^{2}}\right],\end{array}
• das elliptische Hyperparaboloid mit der Zugehörigkeitsfunktion \begin{array}\mu ({x}_{1},\ldots,{x}_{n})=\mu (\bf x)=\\ \,\,\,\,\,=\max [0,1-(\bf x-\bar{\bf x})^T B(x-\bar{x})]\end{array} mit einer positiv definiten (n × n)-Matrix B.