Lexikon der Mathematik: ganzzahlige lineare Optimierung
Lösungstheorie von linearen Optimierungsproblemen, bei denen die Variablen des Problems nur ganzzahlige Werte annehmen dürfen.
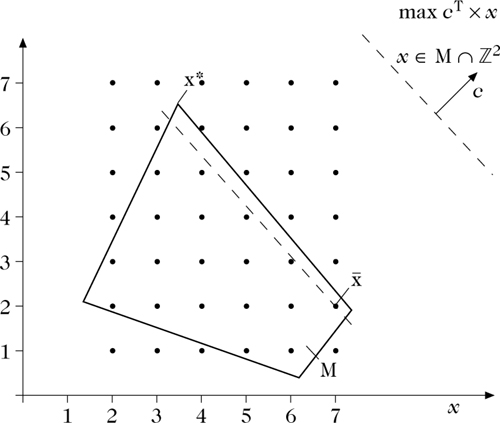
Ganzzahlige lineare Optimierung: Die dem Minimalpunkt \(\bar{x}\in M\cap\mathbb{Z}^{2}\) des ganzzahligen Problems am nächsten liegende Ecke von M muß nicht die optimale Ecke x* des Problems min cTx, x ∈ M, sein.
Die meisten Ergebnisse beziehen sich auf rationale Eingabedaten. Eines der wesentlichen Probleme bei der Lösung derartiger Aufgaben ist das Fehlen eines befriedigenden Dualitätssatzes; für den üblichen Dualitätssatz der linearen Optimierung führt die Forderung nach Ganzzahligkeit der Variablen i. a. zu einer positiven Dualitätslücke. Als algorithmische Konsequenz dieses Sachverhalts sind ganzzahlige lineare Optimierungsprobleme vermutlich schwieriger zu lösen als lineare Optimierungsprobleme ohne zusätzliche Forderung an die Ganzzahligkeit der Variablen. So ist das Entscheidungsproblem: „Gegeben ein System A · x ≤ b mit A ∈ ℚm×n, b ∈ ℚm; gibt es eine Lösung \(\bar{x}\in \mathbb{Z}^{n}\)“ NP-vollständig (im Gegensatz zur Suche einer Lösung in ℚn, die in Polynomzeit ausführbar ist). Eine Ausnahme bildet die Teilmenge ganzzahliger linearer Optimierungsprobleme, bei denen alle Eingabedaten ganzzahlig sind und die Matrix A unimodular ist (d. h. für alle quadratischen Untermatrizen von A hat die Determinante einen Wert in {−1, 0, 1}). Diese Probleme haben immer ganzzahlige Lösungen, welche auch effizient gefunden werden können (bzgl. des Modells der Turingmaschine). Wichtige Lösungsverfahren für ganzzahlige lineare Probleme sind Schnittebenenverfahren wie dasjenige von Gomory.
Man vergleiche auch den Artikel Ganzzahlige Optimierung.
[1] Schrijver, A.: Theory of linear and integer programming. John Wiley and Sons, 1986.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.