Lexikon der Mathematik: Gaußsche Fehlerfunktion
Fehlerfunktion, die durch
Ebenso definiert man die reziproke Fehlerfunktion durch
Der Integrationsweg des Integrals muß hierbei in der komplexen Ebene so gewählt werden, daß
Es ist erf eine ganze Funktion, für die die folgenden elementaren Symmetrierelationen gelten:
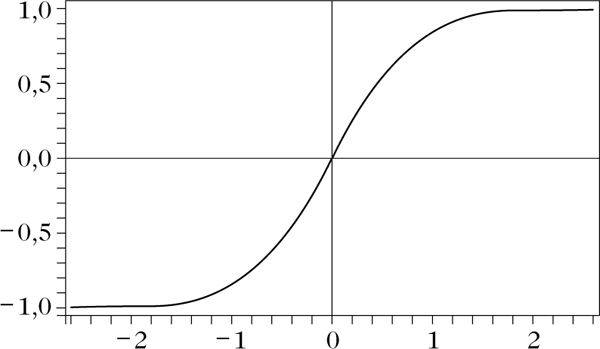
Die Gaußsche Fehlerfunktion
Man erhält ferner als Reihenentwicklungen:
Für x ≥ 0 gelten die folgenden, oft nützlichen Ungleichungen:
Ferner gilt die folgende asymptotische Entwicklung für z → ∞, wobei \(|\arg (z)|\space \lt \space \frac{3\pi }{4}\):
Für x ∈ ℝ ist erf reellwertig, und es gilt
Die Gaußsche Fehlerfunktion spielt eine wichtige Rolle in der Fehlerrechnung. Eine aus n Messungen derselben physikalischen Größe bestehende Beobachtungsreihe a1, a2, …, an ist in der Regel mit Beobachtungsfehlern ϵ1, ϵ2,…, ϵn behaftet. Ist x der wahre Wert, so gilt
Unter gewissen Voraussetzungen unterliegen die Beobachtungsfehler ϵv einer strengen Gesetzmäßigkeit, und zwar dem sog. Gaußschen Fehlerverteilungsgesetz: Die Wahrscheinlichkeit P(Δ) dafür, daß ein Beobachtungsfehler ϵ zwischen den Schranken −Δ und Δ (Δ > 0) liegt, ist gegeben durch
Schließlich sei der enge Zusammenhang
[1] Abramowitz, M.; Stegun, I.A.: Handbook of Mathematical Functions. Dover Publications, 1972.
[2] Olver, F.W.J.: Asymptotics and Special Functions. Academic Press, 1974.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.