H.J. Prömel

Die Graphentheorie als eigenständiges Forschungsgebiet ist noch recht jung, obwohl einige ihrer Wurzeln mehr als zweihundertfünfzig Jahre zurückreichen. Mitte des neunzehnten Jahrhunderts bekam sie einen starken Impuls aus den sich zu jener Zeit schnell entwickelnden Naturwissenschaften. So enthalten Kirchhoffs Arbeit über elektrische Netzwerke 1847 und Cayleys Anzahluntersuchungen von chemischen Verbindungen in den 70er und 80er Jahren des neunzehnten Jahrhunderts grundlegende Resultate der Graphentheorie. James Joseph Sylvester benutzte 1878 in seiner Arbeit Chemistry and Algebra erstmalig das Wort „Graph“ als Abkürzung für graphische Darstellungen, wie sie in der Chemie benutzt werden. Eine erste Monographie über die Anfänge der Theorie der endlichen und unendlichen Graphen hat der ungarische Mathematiker Dénes König (1884-1944) Mitte der dreißiger Jahre des zwanzigsten Jahrhunderts geschrieben, fast genau zweihundert Jahre nach Leonard Eulers Solutio problematis ad geometriam situs pertinentis (1736), einer der ersten graphentheoretischen Arbeit überhaupt, in der der Mathematiker, Physiker und Astronom Euler das Königsberger Brückenproblem studiert und löst.

Heute spielt die Graphentheorie, eingebettet in die diskrete Mathematik, eine herausragende Rolle und ist eines der am schnellsten wachsenden Teilgebiete der Mathematik. Wesentlichen Anteil an der rasanten Entwicklung der Graphentheorie in der zweiten Hälfte des zwanzigsten Jahrhunderts hatte das Bestreben nach einer diskreten Modellierung unserer Welt und der Möglichkeit der Optimierung durch Einzug des Computers. In erster Linie sind hier Probleme aus der Informatik und der diskreten Optimierung zu nennen, die sich als graphentheoretische Probleme formulieren und mit graphentheoretischen Methoden lösen lassen. Aber auch in den Ingenieur- und Sozialwissenschaften hat sich die Graphentheorie zu einem unverzichtbaren Handwerkszeug entwickelt.

Grundlegende Begriffe und Fragestellungen

Ein GraphG ist ein Paar (V, E), wobei V die Menge der Knoten (engl. vertices) des Graphen ist und E ⊆ [V]², eine Teilmenge der zweielementigen Teilmengen von E, die Menge der Kanten (engl. edges) von G ist. Ein Teil des Reizes, den die Graphentheorie ausübt, liegt in der einfachen Visualisierung der zu untersuchenden Objekte. Der Kantengraph des Dodekaeders, einer der Platonischen Graphen, ist in Abbildung 1 dargestellt. Die Knoten sind dabei durch Punkte in der Ebene repräsentiert und je zwei Knoten, die eine Kante bilden, durch eine Linie verbunden.

Eulersche Graphen, Hamiltonkreise und das Travelling Salesman Problem

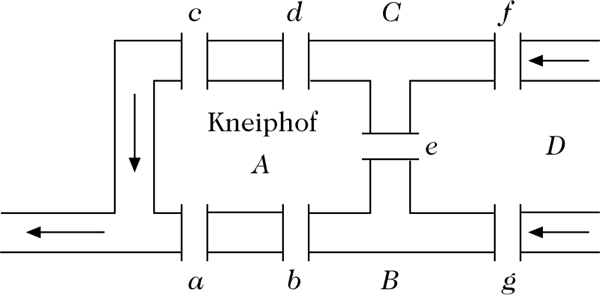
In der Stadt Königsberg führten Mitte des siebzehnten Jahrhunderts sieben Brücken über den Pregel, der dort, wie die Abbildung 2 zeigt, den Kneiphof umschließt.

Die Frage, die über den damaligen Bürgermeister der Stadt Danzig, Carl Leonhard Gottlieb Ehler, an Euler herangetragen wurde, war die, ob es einen Rundgang durch Königsberg gäbe, der jede der Brücken genau einmal benutzt. Die Antwort auf diese Frage erachtete Euler als wichtig genug, um ihr 1736 die oben erwähnte dreizehnseitige Abhandlung zu widmen. Repräsentiert man die Brücken durch Kanten in einem Graphen, so erhält man eine Darstellung des Problems durch einen Graphen (Abbildung 3), wobei es sich bei der einfachen Repräsentation links um einen sogenannten Multigraphen (zwei Knoten können mehr als eine Kante bilden) handelt. Euler zeigte, daß es keinen Rundgang der gewünschten Art geben kann, da die Graphen in Abbildung 3 jeweils Knoten ungeraden Grades besitzen, das heißt Knoten, deren Anzahl Nachbarn ungerade ist. Mehr noch, Euler behauptete, daß ein Graph genau dann einen geschlossenen Weg besitzt, der jede Kante genau einmal durchläuft, heute sagt man, daß er Eulersch ist, wenn jeder Knoten des Graphen geraden Grad besitzt (Eulerscher Graph). Eulers Intuition erwies sich als richtig, auch wenn ein vollständiger Beweis dieser Aussage erstmals von Carl Fridolin Bernhard Hierholzer 1873 gegeben wurde.

Aus heutiger Sicht und für vielfältige Anwendungen ist von besonderem Interesse, daß die Eigenschaft eines Graphen, Eulersch zu sein, algorithmisch einfach zu handhaben ist. Aus dem Beweis von Hierholzer ergibt sich ein linearer Algorithmus, das heißt ein Verfahren, dessen Laufzeit durch eine lineare Funktion in der Länge der Eingabe des Problems beschränkt ist und das entscheidet, ob ein gegebener Graph Eulersch ist. Wenn dies der Fall ist, findet der Algorithmus zudem einen Eulerkreis, also einen geschlossenen Weg durch den Graphen, der jede Kante genau einmal durchläuft. Damit ist die Eigenschaft, Eulersch zu sein, eine algorithmisch schnell zu testende Grapheneigenschaft.

Scheinbar eng mit dem Problem, einen geschlossenen Weg durch einen Graphen zu finden, der jede Kante genau einmal durchläuft, ist das Problem, einen geschlossenen Weg zu finden, der jeden Knoten genau einmal durchläuft. Ein solcher Kreis in einem Graphen heißt nach dem irischen Mathematiker Sir William Rowan Hamilton (1805– 1865) ein Hamiltonkreis. Hamilton „erfand“ 1857 ein Spiel, welches unter anderem das Auffinden eines Hamiltonkreises in dem Kantengraphen des Dodekaeders (siehe Abb. 1) verlangt. Während es in diesem Beispiel noch einfach ist, einen Hamiltonkreis zu finden, und dem Spiel, das Hamilton für 25 Pfund an einen Spielehändler verkaufte, deshalb kein großer Erfolg beschieden war, erweist es sich im allgemeinen als schwer zu entscheiden, ob ein gegebener Graph einen Hamiltonkreis enthält. Die vollständige Enumeration aller mögli-chen Knotenfolgen mit dem anschließenden Test, ob eine Knotenfolge einen Hamiltonkreis bildet, ist bis heute – cum grano salis – die schnellste Strategie zu entscheiden, ob ein gegebener Graph einen Hamiltonkreis besitzt. Richard Karp bewies zudem 1972, daß dieses Problem zu der Klasse der NP-vollständigen Probleme gehört. Für kein Problem in dieser viele tausend Probleme umfassenden Klasse ist bis heute ein polynomialer Lösungsalgorithmus bekannt, und würde man für nur eins dieser Probleme einen solchen finden, hätte man bereits gezeigt, daß es für jedes Problem in der Klasse einen polynomialen Algorithmus gibt. Im Gegensatz zum Eulerkreisproblem ist das Hamiltonkreis-problem also ein algorithmisch schwer zu lösendes Problem. Eine entsprechend wichtige Rolle spielt in der Graphentheorie das Auffinden hinreichender Kriterien für die Existenz von Hamiltonkreisen in Graphen.

Einer breiteren Öffentlichkeit bekannt geworden ist das Hamiltonkreisproblem durch seine Optimierungsvariante, dem Problem des Hand-lungsreisenden oder Travelling Salesman Problem, das erstmals von Karl Menger (1902–1985) in einem Vortrag 1930 als „Botenproblem“ formuliert wurde: Ein Handlungsreisender möchte n Städte besuchen und wieder an seinen Ausgangspunkt zurückkehren. Eine Fahrt zwischen den Städten i und j verursacht Kosten in Höhe von c_ij Einheiten. Der Handlungsreisende ist bemüht, eine Rundreise zu finden, die seine Reisekosten minimiert. In die Sprache der Graphentheorie übertragen liest sich das Problem wie folgt: Gegeben sei ein vollständiger Graph auf n Knoten, der mit K_n bezeichnet wird, mit zusätzlichen Gewichten oder Längen auf den Kanten. Gesucht wird ein kürzester Hamiltonkreis in diesem Graphen. Dieses Problem, von dem sich leicht zeigen läßt, das es mindestens so schwer ist wie das Problem, einen Hamiltonkreis in einem gegebenen Graphen zu finden (solche Probleme heißen NP-schwer), hat in den vergangenen Jahren eine große Aufmerksamkeit erfahren. Neben seiner Anwendungsrelevanz ist das Travelling Salesman Problem ein wichtiges Testproblem für die Qualität (nicht-polynomialer) Optimierungsalgorithmen geworden. Inzwischen ist man in der Lage, mit Hilfe intelligenter Enumerationsverfahren und schneller Computer das Travelling Salesman Problem für Graphen mit mehr als 10.000 Knoten optimal zu lösen. Eine Alternative dazu, die beste Lösung finden zu wollen, besteht darin, eine „gute“ Lösung zu akzeptieren, die schnell (was hier in polynomialer Zeit heißen soll) gefunden werden kann. Sanjeev Arora zeigte 1996, daß sich die optimale Lösung eines euklidischen Travelling Salesman Problems (das heißt der zugrunde liegende Graph hat geographische Kantenlängen), die zu finden auch schon NP-schwer ist, in polynomialer Zeit beliebig genau approximieren läßt. Mit anderen Worten, zu jedem ϵ > 0 gibt es einen polynomialen Algorithmus, der zu einem gegebenen euklidischen Travelling Salesman Problems eine Rundreise findet, deren Länge höchstens um einen Faktor (1+ϵ) länger ist, als die (nicht bekannte!) Länge einer kürzesten Rundreise. Nicos Christofides zeigte 1976, daß sich die optimale Lösung des Travelling Salesman Problems in einem Graphen, dessen Kantenlängen der Dreiecksungleichung genügen, zumindest bis auf den Faktor 3/2 in polynomialer Zeit approximieren läßt. Für das allgemeine Travelling Salesman Problem ist das beweisbar unmöglich, es sei denn, alle NP-vollständigen Probleme lassen sich in polynomialer Zeit lösen.

Planarität, Einbettungen und Minoren

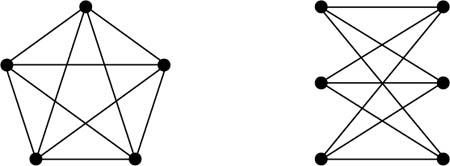
Ein Graph heißt planar, falls er so in die Ebene (oder auf eine Kugel) gezeichnet werden kann, daß sich verschiedene Kanten nicht kreuzen, das heißt, nur in Knoten berühren. Der Dodekaeder-Graph ist, wie Abbildung 1 zeigt, planar. Ein planarer Graph G = (V, E, R) zusammen mit einer planaren Repräsentation in die Ebene heißt ebener Graph. R bezeichnet dabei die Gebiete (engl. regions) von G in der gegebenen Einbettung. Euler bewies 1752 die nach ihm benannte Polyederformel: Für jeden ebenen Graphen gilt |V|−|E|+|R|= 2. Allgemeiner gilt für jede orientierbare 2-dimensionale geschlossene Fläche S (diese Flächen sind bis auf Homöomorphie gerade die Kugeln mit h Henkeln für h ≥ 0) und für jeden Graphen G = (V, E), der sich in S, aber nicht in eine Fläche kreuzungsfrei einbetten läßt, die homöomorph zu einer Kugel mit weniger Henkeln ist als S, daß |V| − |E|+|R|= e(S), wobei e(S) die Euler-Charakteristik von S ist. Es läßt sich zeigen, daß e(S) = 2 − 2h, wenn S homöomorph zur Kugel mit h Henkeln ist. Es ist eine beliebte unterhaltungsmathematische Aufgabe nachzuweisen, daß der K₅ und der K_3,3 (siehe Abb. 4) keine kreuzungsfreie Einbettung in die Ebene besitzen.

Aus der Eulerschen Polyederformel läßt sich unmittelbar ein formaler Beweis für diesen Sachverhalt ableiten. Fügt man zusätzliche Knoten auf den Kanten des K₅ oder des K_3,3 ein, so ist der resultierende Graph eine Unterteilung des K₅ oder des K_3,3. Kazimierz Kuratowski (1896–1980) verband Topologie und Graphentheorie, indem er 1930 bewies, daß ein Graph G genau dann planar ist, wenn er keine Unterteilung des K₅ oder des K_3,3 als Subgraphen enthält. Klaus Wagner (1910–2000) zeigte 1937, daß eine analoge Charakterisierung auch gilt, verwendet man den Begriff des Minoren anstatt des (restriktiveren) Begriffs des topologischen Subgraphen. Ein Graph G enthält einen Graphen H als Minor, wenn man H aus G durch sukzessives Kontrahieren und Weglassen von Kanten erhalten kann.

Welche Graphen lassen sich in einen Torus (homöomorph zur Kugel mit einem Henkel) und welche in eine Brezelfläche (homöomorph zur Kugel mit zwei Henkeln) einbetten? Eines der bedeutendsten Ergebnisse der letzten beiden Dekaden des zwanzigsten Jahrhunderts in der Graphentheorie ist ein Analogon zum Satz von Wagner für Flächen mit kleinerer Euler-Charakteristik als der Ebene. Neil Robertson und Paul D. Seymour zeigten in mehreren Arbeiten zwischen 1986 und 1996, daß es zu jeder Fläche S eine endliche Familie F(S) von Graphen gibt, so daß ein Graph G genau dann kreuzungsfrei in S einbettbar ist, wenn er keinen Graphen aus F(S) als Minor enthält. Explizit sind die verbotenen Minoren jedoch bisher für keine orientierbare Fläche außer der Ebene bekannt. Das Problem zu entscheiden, ob ein gegebener Graph planar ist, und ihn in die Ebene einzubetten, wenn dies der Fall ist, ist, wie das Problem, einen Eulerkreis zu finden, ein algorithmisch einfaches Problem. Allgemeiner gilt sogar, daß es zu jeder Fläche S einen linearen Algorithmus gibt, der entscheidet, ob sich ein gegebener Graph kreuzungsfrei in S einbetten läßt, und gegebenenfalls eine solche Einbettung findet.

Die chromatische Zahl, der Vierfarbensatz und Hadwigers Vermutung

Ein sehr populäres Problem der Graphentheorie war das Vierfarbenproblem, das Francis Guthrie 1852 seinem Bruder Frederick, zu der Zeit Student der Mathematik in Cambridge, stellte: Stimmt es, daß die Länder jeder Landkarte stets mit höchstens vier Farben gefärbt werden können, wenn man fordert, daß aneinander grenzende Länder verschiedene Farben erhalten müssen?

Allgemeiner bezeichnet man mit χ(G) die kleinste Zahl von Farben, die benötigt werden, um die Knoten des Graphen G so zu färben, daß je zwei, die eine Kante bilden, verschieden gefärbt sind. χ(G) heißt die chromatische Zahl von G. Offensichtlich gilt χ(K₄) = 4, χ(K₅) = 5 und χ(K_3,3) = 2. In der Sprache der modernen Graphentheorie liest sich nun die Frage von Francis Guthrie wie folgt: Stimmt es, daß χ(G) ≤ 4 für jeden planaren Graphen G gilt? Alfred Bray Kempe (1849–1922) kündigte 1879 in dem Journal Nature eine Lösung des Problems an und publizierte noch im selben Jahr einen vermeintlichen Beweis des Vierfarbensatzes. Kempes Lösung wurde seinerzeit mit großer Euphorie aufgenommen und er selbst zum Fellow der Royal Society gewählt. 11 Jahre später, 1890, fand Percy John Heawood (1861–1955) einen Fehler in Kempes Beweis und korrigierte Kempes Ergebnis zu einem Fünffarbensatz. Heawood zeigte zudem eine obere Schranke für die chromatische Zahl von Graphen G, die sich in eine orientierbare geschlossene Fläche S der Euler-Charakteristik e = e(S) ≤ 1 einbetten lassen: \begin{eqnarray}\chi (G)\le \left\lfloor \frac{7+\sqrt{49-24e}}{2}\right\rfloor =:h(e).\end{eqnarray}

Die Euler-Charakteristik der Ebene, für die Heawoods Beweis nicht gilt, ist 2. Man beachte, daß in diesem Fall χ(G) ≤ 4 resultieren würde. Wie gut ist nun die obere Schranke für die chromatische Zahl, die durch die Heawood-Ungleichung gegeben wird? Heawood selbst glaubte bewiesen zu haben, daß es zu jeder orientierbaren geschlossenen Fläche S mit Euler-Charakteristik ≤ 1 auch einen Graphen G gibt, der sich in S einbetten läßt, und für dessen chromatische Zahl χ(G) = h(e) gilt. Doch Heawoods Beweis war unvollständig und es dauerte noch mehr als 75 Jahre, bevor Gerhard Ringel und J. W. T. Youngs einen vollständigen Beweis dieser als die Heawood-Vermutung bekannt gewordenen Frage geben konnten.

Der Vierfarbensatz wurde 1977 von Kenneth Appel und Wolfgang Haken endgültig bewiesen. Der Beweis beruht auf Ideen, die in rudimentärer Form bereits in Kempes Beweis enthalten sind, und die Mitte des zwanzigsten Jahrhunderts von Heinrich Heesch maßgeblich weiterentwickelt wurden. Appel und Haken zeigten, daß jeder ebene triangulierte Graph mindestens eine von fast 1500 sogenannten „unvermeidbaren Konfigurationen“ enthalten muß. In einem zweiten Schritt wiesen sie dann mit Hilfe eines Computers nach, daß jeder Graph, der eine dieser Konfigurationen enthält, reduzierbar ist, das heißt, eine Vierfärbung des Graphen kann aus der Vierfärbung eines kleineren Graphen hergeleitet werden.

Es ist bekannt, daß es Graphen gibt, die nicht einmal einen K₃, ein Dreieck, als Subgraphen enthalten, jedoch eine beliebig große chromatische Zahl ℓ haben. Eine sehr tiefliegende Vermutung von Hugo Hadwiger, die dieser 1943 aufstellte, besagt, daß jeder Graph G mit χ(G) = ℓ einen K_ℓ als Minor enthält. Für ℓ = 3 und ℓ = 4 ist die Vermutung schon seit langem als richtig bekannt, für ℓ = 5 und ℓ = 6 ist sie äquivalent zum Vierfarbensatz. Für ℓ ≥ 7 konnte sie bisher weder bewiesen noch widerlegt werden. Da man zeigen kann, daß allgemein der Fall ℓ der Vermutung aus dem Fall ℓ + 1 folgt, würde ein Beweis der Hadwiger-Vermutung den Vierfarbensatz in einen allgemeineren Zusammenhang einordnen.

Die chromatische Zahl eines Graphen ist wie die Eigenschaft, ob ein gegebener Graph einen Hamilton-Kreis enthält, sehr schwer zu entscheiden. Schon die Frage, ob ein gegebener planarer Graph (von dem wir wissen, daß seine chromatische Zahl höchstens vier ist) die chromatische Zahl drei hat, ist NP-vollständig, das heißt, es ist derzeit kein polynomialer Algorithmus bekannt, der diese Frage beantwortet. Mehr noch, schon die Existenz eines polynomialen Algorithmus, der für ein festes ϵ > 0 entscheidet, ob die chromatische Zahl eines gegebenen Graphen G auf n Knoten kleiner oder gleich k ist, wobei \begin{eqnarray}k\le \chi (G)\cdot {n}^{1/7-{\varepsilon}}\end{eqnarray} ist, impliziert die Existenz eines polynomialen Algorithmus, der die chromatische Zahl von G bestimmt. Unter der Annahme P ≠ NP besagt dieses Resultat, daß sich die chromatische Zahl eines Graphen nicht nur nicht in polynomialer Zeit bestimmen läßt, sondern auch, daß eine vernünftige Approximation dieses wichtigen Parameters in polynomialer Zeit nicht möglich ist.

Extremale Graphen, der Satz von Ramsey und Szemerédis Lemma

Eine grundlegende Frage der extremalen Graphentheorie ist die nach der maximalen Anzahl von Kanten, die ein Graph auf n Knoten haben kann, so daß er eine gegebene Eigenschaft noch besitzt. Aus der Eulerschen Polyederformel folgt beispielsweise unmittelbar, daß die maximale Anzahl von Kanten, die ein planarer Graph auf n Knoten haben kann, 3n − 6 ist. Von zentraler Bedeutung ist insbesondere das Problem, zu einem gegebenen Graphen H die maximale Anzahl ex(n, H) von Kanten zu bestimmen, die ein Graph auf n Knoten höchstens haben kann, wenn er keine Kopie von H als Subgraphen enthält. W. Mantel zeigte bereits 1907, daß ex(n, K₃) = ⌊ n²/4⌋. Der ungarische Mathematiker Paul Turán studierte als erster die Funktion ex(n, K_r) für allgemeines r. Er zeigte 1941, daß \begin{eqnarray}ex(n,\,{K}_{r})=\left(1-\frac{1}{r-1}\right){n}^{2}+o({n}^{2}).\end{eqnarray}

Eine tiefliegende Verallgemeinerung des Satzes von Turán bewiesen Paul Erdős und Arthur Harold Stone 1946. Es bezeichne K_r(m) den Graphen auf r · m Knoten, dessen Knotenmenge so in r gleich große Teile zerfällt, daß keine Kante in einem der Teile verläuft, jedoch jedes Knotenpaar mit Knoten aus verschiedenen Teilen eine Kante bildet. Also ist insbesondere K_r(1) = K_r. Erdős und Stone bewiesen nun, daß jeder Graph auf n Knoten für hinreichend großes n, der für beliebig kleines ϵ > 0 (das von n unabhängig ist) nur ϵ · n² mehr als ex(n, K_r) Kanten enthält, nicht nur einen K_r, sondern sogar bereits einen K_r(m) (wobei m = c log n für eine absolute Konstante c gewählt werden kann) als Subgraphen enthält. Dieser Satz wird als der Fundamentalsatz der extremalen Graphentheorie bezeichnet. Eine unmittelbare Konsequenz daraus ist der folgende Zusammenhang zwischen ex(n, H), für einen beliebigen Graphen H, und der chromatischen Zahl von H : \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to \infty }ex(n,\,H){\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}=\frac{\chi (H)-2}{\chi (H)-1}.\end{eqnarray}

Eine weitere Frage von großer Relevanz in der extremalen Graphentheorie ist, wie viele Graphen f(n, H) es (asymptotisch) auf n Knoten gibt, die keine Kopie von H als Subgraphen enthalten. Kolaitis, Prömel und Rothschild gelang es 1986, eine Formel anzugeben, die f(n, K_r) asymptotisch bestimmt. Für beliebiges H mit χ(H) ≥ 3 zeigten Erdős, Frankl und Rödl (1986), daß \begin{eqnarray}f(n,\,H)={2}^{(1+o(1))ex(n,H)},\end{eqnarray} das heißt, sie konnten zumindest eine asymptotische Formel für log₂f(n, H) beweisen. Eine Asymptotik für f(n, H) (falls H ≠ K_r) ist im allgemeinen nicht bekannt. Falls H ein Graph mit χ(H) = 2 ist, konnte selbst eine asymptotische Formel für log₂f(n, H) bisher nicht gezeigt werden.

Es ist eine einfache Beobachtung, daß, wenn auf einer Party sechs Leute zusammenstehen, sich entweder mindestens drei von ihnen paarweise kennen oder sich mindestens drei von ihnen sich paarweise nicht kennen. 1928 bewies Frank Plumpton Ramsey (1903–1930) in seiner Arbeit On a problem of formal logic einen Hilfssatz, der die obige offensichtliche Beobachtung stark verallgemeinert. Ramsey zeigte, daß es zu jeder natürlichen Zahl s eine kleinste natürliche Zahl n = R(s) gibt, so daß es zu jeder Färbung der Kanten des K_n mit 2 Farben, sagen wir mit rot und blau, entweder einen roten K_s-Subgraphen, das heißt, einen K_s-Subgraphen, dessen Kanten alle rot sind, oder einen blauen K_s-Subgraphen des K_n gibt. Wie groß ist nun diese Ramseyfunktion R(s)? Erdős und Szekeres bewiesen bereits 1935, daß \(\begin{eqnarray}R(s)\le {4}^{s}/\sqrt{s}\end{eqnarray}\). Diese Schranke wurde in den folgenden Jahren zwar mehrmals leicht verbessert, jedoch blieb die Asymptotik im Logarithmus unverändert. Eine erste exponentielle untere Schranke für die Ramseyfunktion wurde von Erdős 1947 bewiesen. Er zeigte, daß R(s) ≥ 2^s/2 für alle s ≥ 3. Dieses Ergebnis ist besonders bemerkenswert, da es eines der ersten Resultate in der Graphentheorie war, das unter Zuhilfenahme des Zufalls erzielt wurde. Es löste eine stürmische Entwicklung aus, die letztlich zu einem eigenständigen Teilgebiet der Graphentheorie, der Theorie zufälliger Graphen, führte. Bis heute ist trotz heftigen Bemühens kein konstruktiver Beweis einer exponentiellen unteren Schranke für R(s) bekannt, und auch elaborierte probabilistische Beweismethoden lieferten nur marginale Verbesserungen der Schranke von Erdős. Noch immer ist \begin{eqnarray}\sqrt{2}\lt \mathrm{lim}\,\inf R{(s)}^{1/s}\le \mathrm{lim}\sup \,R{(s)}^{1/s}\lt 4\end{eqnarray} der Stand des Wissens, und selbst die Existenz von lim R(s)^1/s konnte bisher nicht gezeigt werden. Wie das Partybeispiel zeigt, ist R(3) = 6. Wir wissen, daß R(4) = 18 und 43 ≤ R(5) ≤ 49. Paul Erdős, der die extremale Graphentheorie wie kein anderer geprägt hat, schreibt zur Schwierigkeit, diese Zahlen exakt zu bestimmen: „Wenn ein außerirdisches Wesen einmal von den Menschen verlangen würde ‚Entweder ihr sagt mir den Wert von R(5) oder ich vernichte die menschliche Rasse dann wäre es vermutlich die beste Strategie, alle Computer und alle Wissenschaftler dieser Welt an diesem Problem arbeiten zu lassen. Wenn dieses außerirdische Wesen statt nach R(5) nach R(6) fragen würden, wäre es vermutlich die beste Strategie zu versuchen, es zu zerstören bevor es uns zerstört“. Aus Ramseys Hilfssatz, den er Ende der zwanziger Jahre bewies, um die Vollständigkeit eines Modells der Logik erster Stufe nachzuweisen, entwickelte sich die Ramsey Theorie, ein Zweig der Kombinatorik, der weit über die Graphentheorie hinaus reicht. Es sei hier ein weiteres Resultat aus der Ramsey Theorie vermerkt, das fast zeitgleich mit dem Satz von Ramsey bewiesen wurde. Bartel Leendert van der Waerden (1903–1996) bewies 1927 die folgende Aussage: Zu jeder positiven ganzen Zahl s gibt es eine kleinste Zahl W(s), so daß es zu jeder Färbung der positiven ganzen Zahlen von 1 bis W(s) mit zwei Farben, sagen wir mit rot und blau, eine arithmetische Progression der Länge s existiert, deren Elemente entweder alle rot oder alle blau sind. Erdős und Turán vermuteten bereits 1936 eine weitreichende quantitative Verallgemeinerung des Satzes von van der Waerden, nämlich, daß man eine einfarbige arithmetische Progression schon immer in der am häufigsten vorkommenden Farbe finden kann. Genauer formuliert, sie vermuteten, daß jede Teilmenge der natürlichen Zahlen mit positiver oberer Dichte arithmetische Progressionen beliebiger endlicher Länge enthält.

Diese Vermutung wurde 1978 von Endre Szemerédi bewiesen. Als wesentliches Hilfsmittel zum Beweis zeigte er das sogenannte „Regularitätslemma“, ein Satz, der sich in den folgenden Jahren zu einem der wichtigsten Sätze der extremalen Graphentheorie entwickelt hat. Grob gesprochen besagt dieses Resultat, daß sich die Knoten jedes hinreichend großen Graphen so in eine „kleine“ Anzahl gleich großer Teile zerlegen lassen, daß für die meisten Paare dieser Teile gilt, daß die Kanten zwischen ihnen sehr regelmäßig verlaufen – so wie man es erwarten würde, wenn man die Kanten zufällig zwischen die Paare werfen würde. Dieser Satz erlaubt tiefliegende Einsichten in die Struktur von großen Graphen und hat in den vergangenen Jahren weitreichende Konsequenzen auf die Entwicklung der Graphentheorie gehabt.