Größen, zu denen die Funktionswerte konvergieren oder (bei R als Zielbereich) bestimmt divergieren, wenn die Argumentwerte konvergieren oder (bei einer Teilmenge von ℝ als Definitionsbereich) bestimmt divergieren.

Es seien X und Y metrische Räume, D ⊂ X, f : D → Y und a ∈ X Häufungspunkt von D. Dann nennt man b ∈ Y Grenzwert oder Limes von f an der Stelle a, geschrieben \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to a}\,f(x)=b\,\,\,\,\text{oder}\,\,\,f(x)\,\,\to \,\,b\,\,\,(x\,\to \,a),\end{eqnarray}

genau dann, wenn lim_n→∞f(x_n) = b gilt für jede Folge (x_n) in D \{a} mit x_n → a für n →∞, und sagt dann auch „ f(x) konvergiert / strebt gegen b für x gegen a“. Man beachte, daß f an der Stelle a nicht definiert sein muß. Sind d_X, d_Y die Metriken auf X bzw. Y, so hat man lim_x→a f(x) = b genau dann, wenn gilt: \begin{eqnarray}\forall \varepsilon \gt 0\,\,\exists \delta \gt 0\,\forall x\,\in \,D\backslash \,\{a\}({d}_{X}(x,\,a)\lt \delta \,\Rightarrow {d}_{Y}(f(x),\,b)\lt \varepsilon ).\end{eqnarray}

Im Spezialfall normierter Vektorräume (X, ∥∥_X) und (Y, ∥∥_Y) bedeutet dies: \begin{eqnarray}\forall \varepsilon \,\gt \,0\,\exists \delta \,\gt \,0\,\forall x\,\in \,D\,\text{}\,\{a\}\,(\Vert x\,-\,{a\Vert }_{X}\,\lt \,\delta \,\Rightarrow \,\Vert f(x)\,-\,\,{b\Vert }_{Y}\,\lt \,\varepsilon )\,.\end{eqnarray}

f ist genau dann stetig an der Stelle a ∈ D, wenn a isolierter Punkt von D ist oder lim_x→a f(x) = f(a) gilt. Stetigkeit läßt sich auf diese Weise auch definieren (anstatt mit der ϵ-δ-Beschreibung).

Im Fall D ⊂ X = ℝ betrachtet man auch einseitige Grenzwerte. Ist a ∈ ℝ Häufungspunkt von D ∩ (−∞, a), so ist b ∈ Y linksseitiger Grenzwert/ Limes von f an der Stelle a, geschrieben \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to a-}\,f(x)=b\,\,\,\,\text{oder}\,f(x)\,\to \,b\,\,(x\,\to \,a-),\end{eqnarray}

genau dann, wenn lim_n→∞f(x_n) = b gilt für jede Folge (x_n) in D ∩ (−∞, a) mit x_n → a für n →∞. Neben lim_x→a−f(x) sind auch die Bezeichnungen \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to a-0}\,f(x),\,\mathop{\mathrm{lim}}\limits_{x\uparrow a}\,f(x),\,f(a-),\,f(a\,-\,0)\end{eqnarray}

gebräuchlich. f ist genau dann linksseitig stetig an der Stelle a, wenn a isolierter Punkt von D ∩ (−∞, a) ist oder f(a−) = f(a) gilt.

Entsprechend ist, wenn a ∈ ℝ Häufungspunkt von D ∩ (a, ∞) ist, b rechtsseitiger Grenzwert/ Limes von f an der Stelle a, geschrieben \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to a+}\,f(x)=b\,\,\,\,\text{oder}\,f(x)\,\to \,b\,\,(x\,\to \,a+),\,\,\end{eqnarray}

genau dann, wenn lim_n→∞f(x_n) = b gilt für jede Folge (x_n) in D ∩ (a, ∞) mit x_n → a für n →∞. Neben lim_x→a+f(x) sind auch die Bezeichnungen \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to a+0}\,f(x),\,\mathop{\mathrm{lim}}\limits_{x\downarrow a}\,f(x),\,f(a+),\,f(a\,+0)\end{eqnarray}

üblich. f ist genau dann rechtsseitig stetig an der Stelle a, wenn a isolierter Punkt von D ∩ (a, ∞) ist oder f(a+) = f(a) gilt

Ist a ∈ D Häufungspunkt von D ∩ (−∞, a) und von D ∩ (a, ∞), so ist f genau dann stetig an der Stelle a, wenn f(a−) = f(a) = f(a+) gilt. Ist f nicht stetig an einer solchen Stelle a, so muß also einer der folgenden Fälle vorliegen:

• f(a−) und f(a+) existieren beide und sind gleich, aber verschieden von f(a).
• f(a−) und f(a+) existieren beide, sind aber verschieden voneinander.
• f(a−) und f(a+) existieren nicht beide. In den ersten beiden Fällen heißt a Unstetigkeitsstelle erster Art oder Sprungstelle von f. Im ersten Fall heißt a auch Einsiedlerpunkt von f, und man sagt, f habe an der Stelle a eine hebbare Unstetigkeit. Im zweiten Fall ist die Unstetigkeit nicht hebbar, und man nennt f(a+) − f(a−) den Sprung von f an der Stelle a. Im dritten Fall heißt a Unstetigkeitstelle zweiter Art von f. Monotone Funktionen auf abgeschlossenen Intervallen besitzen keine Unstetigkeitsstellen zweiter Art, d. h. sie haben links-und rechtsseitige Grenzwerte an allen Stellen, an denen diese Begriffe sinnvoll sind. Ferner haben sie höchstens abzählbar viele Sprungstellen.

Ist D ⊂ X = ℝ nach oben unbeschränkt, so nennt man b ∈ Y Grenzwert oder Limes von f(x) für x →∞, geschrieben \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to \infty }\,f(x)=b\,\,\,\,\text{oder}\,f(x)\,\to \,b\,\,(x\,\to \,\infty ),\end{eqnarray}

genau dann, wenn lim_n→∞f(x_n) = b gilt für jede Folge (x_n) in D mit x_n →∞ für n →∞, und sagt dann auch „ f(x) konvergiert / strebt gegen b für x gegen Unendlich“. Man hat genau dann lim_x→∞f(x) = b, wenn gilt \begin{eqnarray}\forall \varepsilon\,\gt \,0\,{\exists }_{x0}\,\in \,{\mathbb{R}}\,\,\forall x\,\in \,D\,(x\,\gt \,{x}_{0}\,\Rightarrow \,|f(x)\,-\,b|\,\lt \,\varepsilon).\,\end{eqnarray}

Entsprechend wird lim_x→−∞f(x) = b definiert, wenn D nach unten unbeschränkt ist. Auch hier hat man eine (1) entsprechende Charakterisierung. Das Monotoniekriterium besagt bei nach oben unbeschränktem D: Ist f isoton und nach oben beschränkt oder antiton und nach unten beschränkt, so existiert lim_x→∞f(x). Entsprechendes gilt bei nach unten unbeschränktem D für lim_x→−∞f(x).

Im Fall Y = ℝ betrachtet man auch bestimmte Divergenz von f(x) gegen ∞ und −∞: Ist a Häufungspunkt von D, so nennt man ∞ Grenzwert oder Limes von f an der Stelle a, geschrieben \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to a}\,f(x)=\infty \,\,\,\,\text{oder}\,\,\,\text{f}(x)\,\,\to \,\,\infty \,\,\,(x\,\to \,a),\end{eqnarray}

genau dann, wenn lim_n→∞f(x_n) = b gilt für jede Folge (x_n) in D mit x_n →∞ für n →∞, und sagt dann auch „ f(x) (bestimmt) / strebt gegen Unendlich für x gegen a“. Man hat genau dann \(\mathop{\mathrm{lim}}\limits_{x\to a}\,f(x)=\infty \), wenn gilt \begin{eqnarray}\forall K\,\gt \,0\,\exists \delta \,\gt \,0\,\forall x\,\in \,D\,(|x\,-\,a|\,\lt \,\delta \,\Rightarrow \,f(x)\,\gt \,K)\end{eqnarray}

Demgemäß wird auch bestimmte Divergenz von f(x) gegen −∞ erklärt. Gilt auch X = R, so definiert man entsprechend ∞ und −∞ auch als links- und rechtsseitige Grenzwerte von f(x) an einer Stelle a ∈ X und für x → ±∞ und bezeichnet ∞ und −∞ dann als uneigentliche Grenzwerte.

Aus den Grenzwertsätzen für Zahlenfolgen erhält man im Fall X = Y = ℝ entsprechende Aussagen über das Grenzwertverhalten von f(x) sowohl im Fall der Konvergenz als auch bei bestimmter Divergenz.

Im Fall eines vollständigen Raums Y, insbesondere bei Y = R, kann die Existenz von lim_x→a f(x), wobei a ∈ X wieder ein Häufungspunkt von D sei, auch ohne Kenntnis des Grenzwerts mit dem Cauchy-Kriterium untersucht werden, das besagt, daß lim_x→a f(x) in Y genau dann existiert, wenn gilt: \begin{eqnarray}\forall \varepsilon \,\gt \,0\,\exists \delta \gt0\,\forall {x}_{1},\,{x}_{2}\,\in \,D\backslash \,\{a\}\,({\delta}_{X}({x}_{1},\,a)\lt \delta \,\wedge \,{\delta }_{X}({x}_{2},\,a)\lt \delta \,\Rightarrow \,{\delta }_{Y}(f({x}_{1}),\,f({x}_{2}))\lt \varepsilon).\end{eqnarray}

Ist noch X = ℝ, so kann ein Cauchy-Kriterium auch für die Grenzwerte von f(x) für x → ±∞ formuliert werden. Bei nach oben unbeschränktem D ⊂ X besagt es beispielsweise, daß lim_x→∞f(x) in Y genau dann existiert, wenn gilt: \begin{eqnarray}\forall \varepsilon \,\gt \,0\,\exists {x}_{0}\,\in \,{\mathbb{R}}\,\forall {x}_{1},\,{x}_{2}\,\in \,D\,({x}_{1},\,{x}_{2}\,\gt \,{x}_{0}\,\Rightarrow \,|f({x}_{1})\,-\,f({x}_{2})|\,\lt \,\varepsilon ).\end{eqnarray}

Wie beim Grenzwert einer Zahlenfolge kann man auch die Kriterien für die Grenzwerte von Funktionen einheitlich mittels ϵ-Umgebungen formulieren. Man hat lim_x→a f(x) = b genau dann, wenn gilt: \begin{eqnarray}\forall \,\varepsilon \,\gt \,0\,\exists \delta \,\gt \,0\,f({U}_{a}^{\delta })\,\subset \,{U}_{b}^{\varepsilon }\end{eqnarray}

Dies gilt sowohl für Häufungswerte a ∈ X von D als auch im Fall X = ℝ bei nach unten bzw. oben unbeschränktem D für a = −∞ bzw. a = ∞ und im Fall Y = R für b ∈ {−∞, ∞}, wenn man für ϵ = 0 definiert: \begin{eqnarray}{U}_{-\infty }^{\varepsilon }=\{x\,\in \,{\mathbb{R}}\,|\,x\,\lt \,-\,\frac{1}{\varepsilon }\},\\ \,{U}_{\infty }^{\varepsilon }=\{x\,\in \,{\mathbb{R}}\,|\,x\,\,\gt \,\frac{1}{\varepsilon }\}\,.\end{eqnarray}

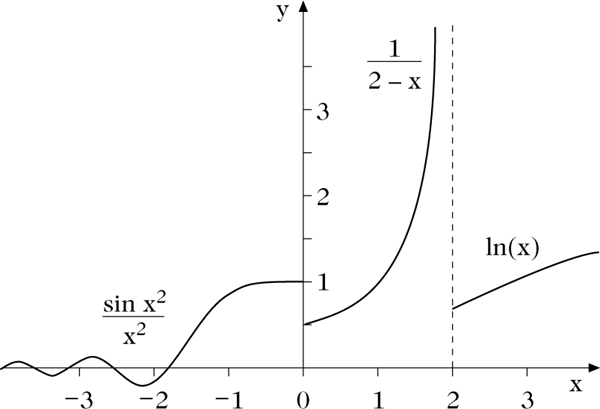
Beispiele der oben betrachteten Arten von Grenzwerten sind zu ersehen an der Funktion f : ℝ → ℝ mit \begin{eqnarray}f(x)=\left\{\begin{array}{c}\frac{\sin {x}^{2}}{{x}^{2}}\,\,,\,\,\,x\,\lt \,0,\\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,x=\text{0},\\ \frac{1}{2-x}\,\,\,\,,\,\,\,0\,\lt \,x\,\lt \,2,\,\,\\ \text{In}(x)\,\,\,,\,\,\,x\,\ge \,2.\end{array}\right.\end{eqnarray}

Es gilt f(x) → 0 für x → −∞ und f(x) →∞ für x →∞. Ferner ist f(0−) = f(0) = 1, d. h. f ist linksseitig stetig an der Stelle 0. Wegen f(0+) = ¹₂ ist f nicht rechtsseitig stetig an der Stelle 0. Weiter ist f(2−) = ∞ und f(2) = f(2+) = ln(2), d. h. f ist nicht linksseitig, aber rechtsseitig stetig an der Stelle 2. Außer an den Stellen 0 und 2 ist f stetig, d. h. f(x−) = f(x) = f(x+) für x ∈ ℝ \ {0, 2}.