Lexikon der Mathematik: Gruppentheorie
Die Gruppentheorie entstand als Verallgemeinerung aus Zahlentheorie und Geometrie und bildet ein Kernstück dessen, was heute als Teilgebiet „Algebra“ der Mathematik behandelt wird.
Eine Gruppe (G, ·) hat ihr Vorbild in der Zahlentheorie wie folgt: Die nichtleere Menge G werde mit der binären Operation „·“ versehen: Für f, g ∈ G ist f · g ∈ G und heißt das Produkt von f und g. Dabei kann „·“ sowohl für Addition als auch für Multiplikation stehen.
Beipiele: Sowohl die reellen Zahlen mit Addition (ℝ, +) als auch die positiven reellen Zahlen mit Multiplikation (ℝ+, ·) bilden eine Gruppe. Der natürliche Logarithmus bildet dann einen Gruppenisomorphismus zwischen diesen beiden Gruppen: ln : ℝ+ → ℝ, der das Logarithmengesetz ln (ab) = ln (a) + ln (b) widerspiegelt.
In der Geometrie hat die Gruppe ihren Ursprung in der Bewegung geometrischer Objekte; das wichtigste Beispiel ist die Drehgruppe des dreidimensionalen euklidischen Raums. (Heute wird die Menge aller Bewegungen Transformationsgruppe genannt.) An diesem Beispiel wurde auch erstmals die Bedeutung der Reihenfolge der Einzeltransformationen erkannt. In heutiger Sprache heißt das: Die räumliche Drehgruppe ist nicht abelsch, also nicht kommutativ. Dabei heißt die Gruppe G kommutativ, wenn für alle f, g ∈ G gilt: f · g = g · f.
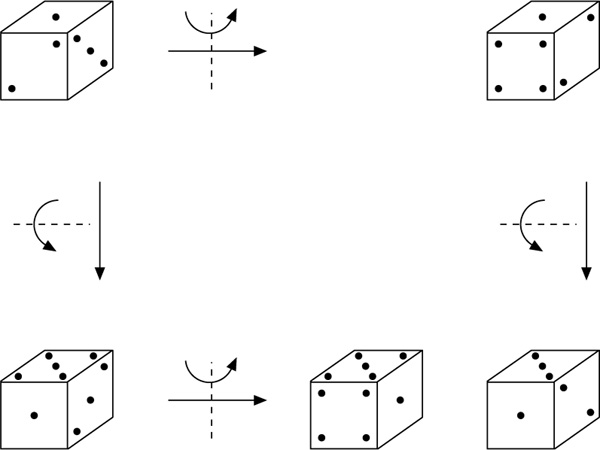
Geometrisch heißt das: Wenn der Standardspielwürfel, bei dem die Summe der Augen gegenüberliegender Seiten stets gleich 7 ist, erst um die vertikale und danach um die horizontale Achse um jeweils 900 gedreht wird, ist seine Lage hinterher anders, als wenn erst um die horizontale und danach um die vertikale Achse gedreht wird.
Veranschaulichung der Nichtkommutativität der räumlichen Drehgruppe
Die drei Gruppenaxiome sind wie folgt motiviert:
- Assoziativität: (f · g) · h = f · (g · h). Werden h, g und f als drei nacheinander auszuführende Transformationen interpretiert, dann soll das Gesamtergebnis nicht davon abhängen, ob man sich das Zwischenergebnis nach einer oder erst nach zwei Operationen „anschaut“.
- Existenz eines neutralen Elements e: e · g = g · e = g. Die identische Transformation soll nichts am Objekt ändern, und sie soll stets als Bestandteil der Gruppe gelten.
- Existenz eines inversen Elements: g · g−1 = g−1 · g = e. Zu jeder Transformation soll eine eindeutig bestimmte Umkehrtransformation existieren. Auch bei nichtkommutativen Gruppen definieren die beiden Gleichungen g · g−1 = e und g−1 · g = e dasselbe inverse Element g−1 zu g.
Die Gruppentheorie unterteilt sich in verschiedene Teilgebiete, die sich durch die folgenden Bezeichnungen grob charakterisieren lassen: endliche Gruppe, Permutationsgruppe, Galois-Gruppe, zyklische Gruppe, endlich erzeugte Gruppe, kristallographische Gruppe, diskrete Gruppe, topologische Gruppe, Lie-Gruppe, Körper.
In jedem dieser Teilgebiete ist die Klassifikation von Gruppen eine wichtige Aufgabe, und dazu ist die Untersuchung der Charaktere einer Gruppe nötig.
Folgende Begriffe werden in der Gruppentheorie verwendet: Untergruppe, Normalteiler, Faktorgruppe, Darstellung von Gruppen.
Im einzelnen: H ist eine Untergruppe der Gruppe (G, ·), wenn H eine solche Teilmenge von G ist, für die (H, ·) eine Gruppe ist. Die beiden stets existierenden Untergruppen von G sind G selbst und die einelementige Gruppe {e}. Für bestimmte Gruppen, die nur „wenige“ Untergruppen besitzen, ist der Begriff der einfachen Gruppe geprägt worden.
Mittels Normalteiler und Faktorgruppe wird die Gruppenklassifikation möglich. Für die Darstellung von Gruppen Darstellung einer Lie-Gruppe.
Eine Gruppe heißt endlich, wenn sie endlich viele Elemente enthält. Eine Gruppe, die eine Gruppe von Umordnungen einer endlichen Menge darstellt, heißt Permutationsgruppe. Die Galois-Gruppe stellt die Gruppe der Umordnungen der komplexen Nullstellen eines Polynoms dar, und ihre Struktur gibt Aufschluß darüber, welche algebraischen Gleichungen in geschlossener Form durch eine Lösungsformel aufgelöst werden können, wobei nur die vier Grundrechenarten und das Ziehen der n-ten Wurzel als Bestandteile der Lösungsformel zugelassen sind. Die Gruppe G heißt zyklisch, wenn sie durch ein einziges Element erzeugt wird, d. h. es gibt ein g ∈ G, so daß G selbst die einzige Untergruppe H von G ist, für die g ∈ H gilt. Die Gruppe G heißt endlich erzeugt, wenn es eine endliche Teilmenge J von G gibt, so daß G selbst die einzige Untergruppe H von G ist, für die J eine Teilmenge von H ist.
Führt man neben der Gruppenoperation noch eine weitere Struktur in der Menge G ein, die mit der Gruppenoperation verträglich sein muß, dann gelangt man zu folgenden Begriffen: Ein topologische Gruppe ist eine Gruppe, in der eine Hausdorffsche Topologie so definiert ist, daß sowohl Multiplikation als auch Inversenbildung stetige Abbildungen sind. Ist diese Topologie diskret, so heißt auch die topologische Gruppe diskret.
Ein Körper ist eine Menge, die mit zwei verschiedenen kommutativen Gruppenoperationen versehen ist, welche untereinander durch das Distributionsgesetz verknüpft sind. Genauer: (K, +, ·) ist ein Körper, wenn (K, + ) eine Gruppe mit neutralem Element 0 ist und (K\{0}, ·) ebenfalls eine Gruppe ist, und es gilt für alle k, l, m ∈ K:
Startet man von einem anderen Gesichtspunkt, nämlich dem der freien Gruppe über einem Alphabet, läßt sich die Gruppentheorie auch wie folgt aufbauen: Zunächst wird eine nichtleere Menge M als Alphabet festgelegt, z. B.
Die Elemente von M werden Buchstaben genannt. W ist die Menge aller Wörter. Ein Wort entsteht definitionsgemäß durch das Hintereinanderschreiben von endlich vielen Buchstaben.
Um aus der Menge W eine Gruppe G zu erzeugen, ist noch folgendes zu beachten: Als neutrales Element in der Gruppe G benötigen wir noch das leere Wort, das aus null Buchstaben besteht. Da es ähnlich wie in der Geschichte der römischen Zahlzeichen mit der Bezeichnung der Zahl Null hier Probleme mit der konsistenten Bezeichnung des leeren Worts gibt, wird das leere Wort mit e bezeichnet, wobei e nicht als Buchstabe gilt. Jeder Buchstabe gilt auch schon einzeln als Wort, und das zum Buchstaben a inverse Wort wird mit a−1 bezeichnet. Alle anderen Wörter erhält man dadurch, daß man vorhandene Wörter nebeneinander schreibt. Stehen jedoch ein Buchstabe und sein Inverses nebeneinander, so wird dieses Buchstabenpaar durch e ersetzt. Steht e in einem Wort, so wird e weggelassen.
Beispiel: Die Gruppenoperation werde mit „·“ bezeichnet. Dann ist das Produkt der Wörter ab−1 und ba wie folgt zu bilden: ab−1 · ba = aea = aa
Mit dieser Operation wird G zur Gruppe, und sie heißt die freie Gruppe über M. Ist M endlich, so heißt G endlich erzeugt. Von einer freien Gruppe kann man einen Gruppenhomomorphismus auf eine andere Gruppe wie folgt definieren: Man erklärt bestimmte Relationen, z. B.: „Für jedes Buchstabenpaar a, b gelte ab = ba“, und erhält für dieses Beispiel die freie abelsche Gruppe über M. Für die Klassifikationstheorie von Gruppen ist es wichtig, daß auf diese Weise jede Gruppe als homomorphes Bild einer freien Gruppe entsteht.
Schließlich sei noch erwähnt, daß in der Quantenfeldtheorie die Renormierungsgruppentechnik eine wichtige Rollebeider Regularisierung von Feldsingularitäten spielt. Darin wird die Variation einer Größe, die in der klassischen (= nichtquantisierten) Version der Feldtheorie eine Konstante darstellt, durch eine eindimensionale Lie-Gruppe ausgedrückt.
Literatur
[1] Flachsmeyer, J.; Prohaska, L.: Algebra. Deutscher Verlag der Wissenschaften Berlin, 1980.
[2] Gorenstein, D.: Finite Simple Groups. An Introduction to Their Classification. Plenum Press New York, 1982.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.