Wege in einem Gebiet G ⊂ ℂ, die sich in G stetig ineinander überführen lassen.

Zur präzisen Definition betrachtet man zwei Fälle.

1. Zwei Wege γ₀, γ₁: [0, 1] → G in einem Gebiet G ⊂ ℂ mit gleichem Anfangspunkt a und Endpunkt b heißen homotop in G bei festen Endpunkten (oder kurz FEP-homotop), falls es eine stetige Abbildung ψ: [0, 1] × [0, 1] → G gibt, die folgende Eigenschaften besitzt: \begin{eqnarray}\begin{array}{rl}\psi (0,t)={\gamma }_{0}(t), & \psi (1,t)={\gamma }_{1}(t),\space \space t\in [0,1],\\ \psi (s,0)=a, & \psi (s,1)=b,\space \space s\in [0,1].\end{array}\end{eqnarray}

Die Abbildung ψ heißt eine Homotopie zwischen γ₀ und γ₁. Für jedes s ∈ [0, 1] ist γ_s : [0, 1] → G, t ↦ ψ(s, t) ein Weg in G mit Anfangspunkt a und Endpunkt b. Die Wegeschar (γ_s)_{s∈[0, 1]} nennt man auch eine Deformation des Weges γ₀ in den Weg γ₁.

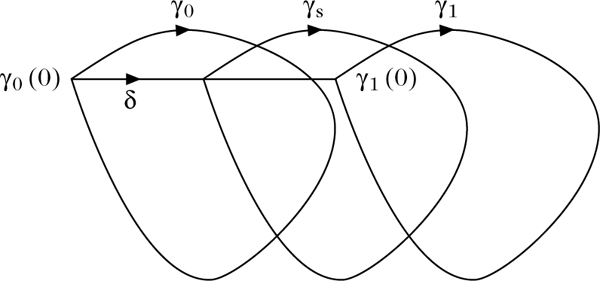
2. Zwei geschlossene Wege γ₀, γ₁ : [0, 1] → G in einem Gebiet G ⊂ ℂ heißen frei homotop in G, falls es eine stetige Abbildung ψ: [0, 1] × [0, 1] → G gibt, die folgende Eigenschaften besitzt: \begin{eqnarray}\begin{array}{c}\psi (0,t)={\gamma }_{0}(t),\space \space \psi (1,t)={\gamma }_{1}(t),\space \space t\in [0,1],\\ \psi (s,0)=\psi (s,1),\space \space s\in [0,1].\end{array}\end{eqnarray}

Dann sind alle Deformationswege γ_s : [0, 1] → G, t ↦ ψ(s, t) geschlossen, und ihre Anfangspunkte durchlaufen in G den Weg δ: [0, 1] → G, s ↦ ψ (s, 0). Die Wege γ₀ und δ + γ₁ − δ haben gleichen Anfangs- und Endpunkt und sind FEP-homotop in G.

Homotope Wege spielen u. a. beim Cauchyschen Integralsatz eine zentrale Rolle.