unendlich ausgedehnte Kurve zweiten Grades mit Mittelpunkt.

I. Hyperbel als Kegelschnitt: Eine Hyperbel ist Schnittfigur einer Ebene ϵ und eines Doppelkegels<?PageNum _454K, falls ϵ nicht durch die Spitze von K verläuft und der Winkel β zwischen ϵ und der Kegelachse kleiner ist als der halbe Öffnungswinkel α des Kegels (Kegelschnitt).

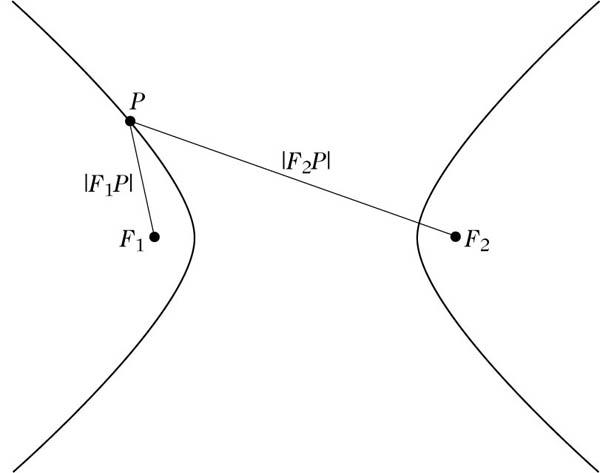
II. Ortsdefinition der Hyperbel: Eine Hyperbel ist die Menge (der geometrische Ort) aller Punkte einer Ebene, für welche die Differenz der Abstände zu zwei festen Punkten F₁ und F₂ gleich einer Konstanten 2a ist (wobei a > 0 sein muß).

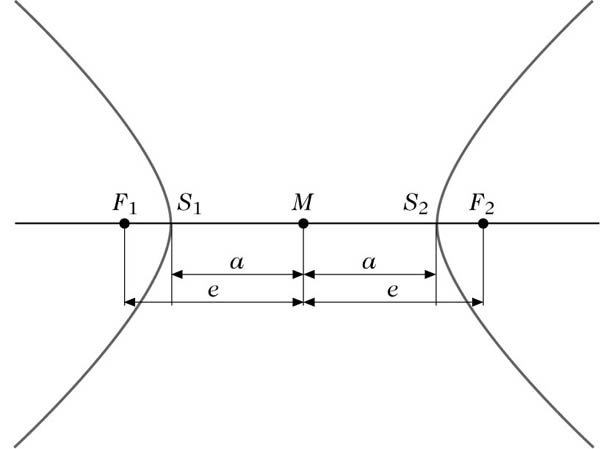
Dabei heißen F₁ und F₂ Brennpunkte, ihr Abstand |F₁F₂| (lineare) Exzentrizität 2e, und der Mittelpunkt der Strecke \begin{eqnarray}\overline{{F}_{1}{F}_{2}}\end{eqnarray} Mittelpunkt der Hyperbel.

Die längere Achse der Hyperbel (die durch die Brennpunkte verläuft) wird als Hauptachse und die dazu senkrechte Achse als Nebenachse bezeichnet. Die Schnittpunkte der Hyperbel mit der Hauptachse sind ihre Scheitel.

Die Hauptachse einer Hyperbel hat die Länge 2a, die Länge 2b der Nebenachse ergibt sich aus der Hauptachsenlänge und der linearen Exzentrizität durch \begin{eqnarray}b=\sqrt{{a}^{2}-{e}^{2}}\end{eqnarray}.

III. Gleichungen der Hyperbel: Wählt man ein kartesisches Koordinatensystem so, daß die x-Achse mit der Hauptachse und die y-Achse mit der Nebenachse der zu beschreibenden Hyperbel zusammenfällt, dann läßt sich eine Hyperbel bezüglich dieses Koordinatensystems durch die Mittelpunktsgleichung \begin{eqnarray}\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1\end{eqnarray} darstellen. Verläuft die x-Achse parallel zur Hauptachse und die y-Achse parallel zur Nebenachse einer Hyperbel und hat der Mittelpunkt dieser Hyperbel die Koordinaten M(x_M; y_M), so wird sie durch eine Gleichung in achsenparalleler Lage beschrieben: \begin{eqnarray}\frac{{(x-{x}_{M})}^{2}}{{a}^{2}}-\frac{{(y-{y}_{M})}^{2}}{{b}^{2}}=1.\end{eqnarray}

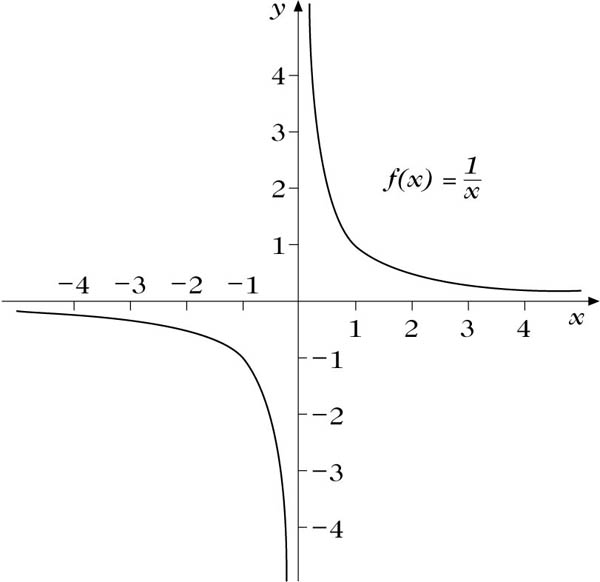
Legt man die Asymptoten einer gegebenen Hyperbel (d. h. die Geraden a₁ und a₂, denen sich die Hyperbel für sehr weit vom Mittelpunkt entfernte Punkte beliebig weit annähert) als Achsen eines Koordinatensystems fest, so läßt sich eine besonders einfache Hyperbelgleichung angeben, die Asymptotengleichung der Hyperbel: \begin{eqnarray}x\cdot y=\frac{{a}^{2}+{b}^{2}}{4}=\frac{{e}^{4}}{4}.\end{eqnarray}

Für den Spezialfall \begin{eqnarray}\frac{{e}^{2}}{4}=1\end{eqnarray} entspricht diese Gleichung gerade der bekannten Gleichung der reziproken Funktion f mit \begin{eqnarray}y=f(x)=\frac{1}{x}\end{eqnarray}, deren Graph eine Hyperbel mit den Koordinatenachsen als Asymptoten ist.

Weiterhin gilt, falls die x-Achse mit der Hauptachse und der Koordinatenursprung mit einem Hauptscheitel der Hyperbel zusammenfällt, die Scheitelgleichung der Hyperbel: \begin{eqnarray}{y}^{2}=2px+\frac{p}{a}\cdot {x}^{2}\quad \text{mit}\quad p=\frac{{b}^{2}}{a}.\end{eqnarray}

Dabei heißt p Halbparameter der Hyperbel und ist gleich der Hälfte der Länge der auf der Hauptachse in einem der Brennpunkte senkrecht stehenden Sehne der Hyperbel.

Schließlich lassen sich die folgenden Hyperbelgleichungen in Polarkoordinaten (r, φ) angeben: \begin{eqnarray}{r}^{2}=\frac{{b}^{2}}{{\varepsilon }^{2}{\cos }^{2}\phi -1}\quad \text{und}\quad r=\frac{p}{1+\varepsilon \cos \phi },\end{eqnarray} wobei der Koordinatenursprung (Pol) bei der ersten Gleichung dem Mittelpunkt der Hyperbel entspricht und bei der zweiten Gleichung in einen der Brennpunkte gelegt wird. Dabei ist \begin{eqnarray}\varepsilon :=\frac{e}{a}\end{eqnarray} mit ϵ > 1 die numerische Exzentrizität der Hyperbel.