Lexikon der Mathematik: hyperbolische Cosekansfunktion
Cosekans hyperbolicus, der Kehrwert der hyperbolischen Sinusfunktion, also die Funktion
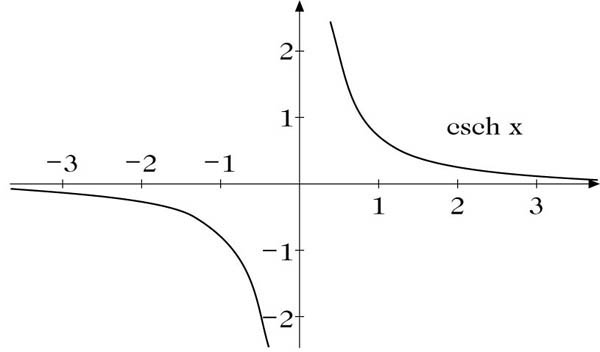
Hyperbolische Cosekansfunktion
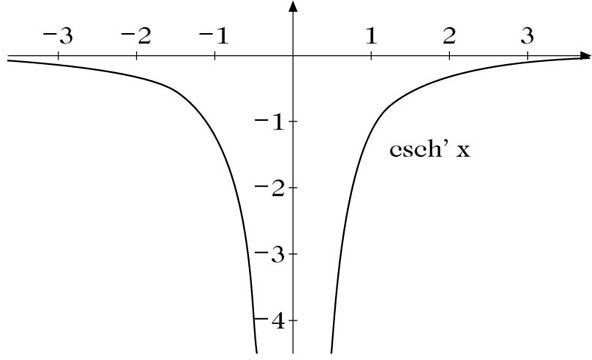
Ableitung der hyperbolischen Cosekansfunktion
für x ∈ ℝ \ {0}. csch ist eine ungerade und differenzierbare Funktion mit
Für 0 < |x| < π hat man die Reihendarstellung
Setzt man die Hyperbelfunktionen und die trigonometrischen Funktionen in die komplexe Ebene fort, so gilt csch iz = −i csc z für z ∈ ℂ. Insbesondere ist die Funktion csch : ℂ \ {kπi | k ∈ ℤ} → ℂ \ {0} 2πi-periodisch. Für z ∈ ℂ mit 0 < |z| < π gilt die obige Reihendarstellung.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.