Lexikon der Mathematik: hyperbolische Cosinusfunktion
Cosinus hyperbolicus, eine der Hyperbelfunktionen, nämlich die durch
Es gilt cosh′ = sinh. cosh erfüllt für x, y ∈ ℝ die Additions- und Summentheoreme
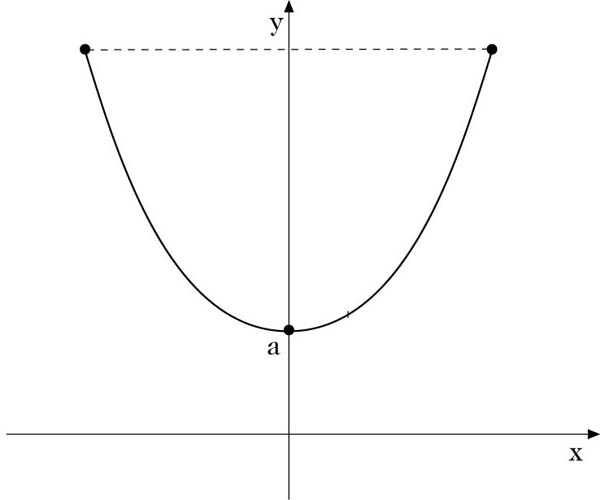
Die Funktion cosh spielt in der Praxis eine wichtige Rolle. Eine an zwei Punkten in gleicher Höhe befestigte freihängende Kette hat unter dem Einfluß der Schwerkraft die Form einer sog. Kettenlinie
Daher bezeichnet man oft auch den Graph der hyperbolischen Cosinusfunktion als Kettenlinie.
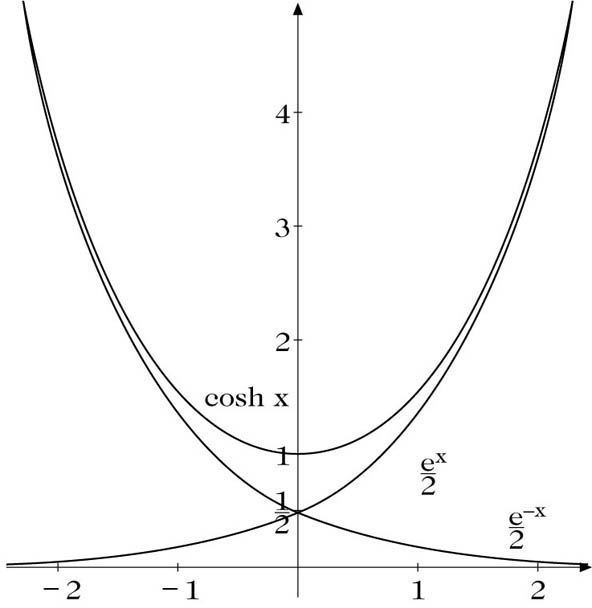
Hyperbolische Cosinusfunktion
Kettenlinie
Für x ∈ ℝ hat man die Reihendarstellung
Es ist cosh2x = sinh2x + 1 für x ∈ ℝ, und für n ∈ ℕ gilt die der de Moivreschen Formel entsprechende Identität
Setzt man die Hyperbelfunktionen und die trigonometrischen Funktionen in die komplexe Ebene fort, so gilt cosh iz = cos z für z ∈ ℂ. Insbesondere ist cosh : ℂ → ℂ 2πi-periodisch. Alle obigen Formeln gelten auch für komplexe Argumente.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.