I.

Als hyperbolische Geometrie oder Lobatschewski-Geometrie wird eine nichteuklidische Geometrie bezeichnet, in der alle Axiome der absoluten Geometrie, also die Axiome der Inzidenz, der Anordnung, der Kongruenz und der Stetigkeit (siehe Axiome der Geometrie), sowie die Verneinung des Parallelenaxioms des Euklid gelten:

Es existiert eine Gerade g und ein nicht auf g liegender Punkt P, durch den mindestens zwei Geraden verlaufen, die mit g in einer Ebene liegen und g nicht schneiden.

Aus diesem Axiom, das auch als Lobatschewskisches Parallelenaxiom bezeichnet wird, und den Axiomen der absoluten Geometrie läßt sich ableiten, daß sogar zu jeder Geraden g und jedem nicht auf g liegenden Punkt P unendlich viele Geraden verlaufen, die mit g in einer Ebene liegen und g nicht schneiden. Allerdings werden nicht alle dieser Geraden als zu g parallel bezeichnet (siehe III.).

Zu der Erkenntnis, daß es eine nichteuklidische Geometrie, basierend auf den Axiomen der absoluten Geometrie und der Negation des euklidischen Parallelenaxioms gibt, gelangten zwischen 1816 und 1832 weitgehend unabhängig voneinander die drei Mathematiker Janos Bolyai, Carl Friedrich Gauss und Nikolai Iwanowitsch Lobatschewski (nichteuklidische Geometrie). Sie lösten damit das seit mehr als zweitausend Jahren bestehende Parallelenproblem auf eine unerwartete Weise, indem sie zeigten, daß das euklidische Parallelenaxiom nicht aus den Axiomen der absoluten Geometrie ableitbar ist.

II. Eigenschaften der hyperbolischen Geometrie

Obwohl sich die euklidische und die hyperbolische Geometrie in ihrer Axiomatik nur um ein einziges Axiom, das Parallelenaxiom, unterscheiden, ergeben sich daraus gravierende Unterschiede beider Geometrien in wichtigen Eigenschaften. Zu den interessantesten Eigenschaften der hyperbolischen

Geometrie, die von denen der euklidischen Geometrie abweichen, gehören die folgenden:

• Die Innenwinkelsumme eines jeden Dreiecks ist kleiner als 180°.
• Es existiert kein spitzer Winkel, für den alle in beliebigen Punken eines seiner Schenkel errichteten Senkrechten den anderen Schenkel treffen.
• Abstandslinien sind keine Geraden, d. h. die Menge aller Punkte, die von einer gegebenen Geraden g denselben positiven Abstand haben und in einer durch g begrenzten Halbebene liegen, ist in keinem Fall eine Gerade.
• Zwei Dreiecke, die paarweise in allen drei Winkeln übereinstimmen, sind kongruent. Es existieren also keine ähnlichen und dabei nicht kongruenten Dreiecke.
• Drei Punkte, die nicht auf einer Geraden liegen, gehören nicht in jedem Falle einem Kreis an; im Raum wird durch vier nicht auf einer Ebene liegende Punkte nicht notwendigerweise eine Kugel bestimmt.

III. Parallele und divergierende Geraden

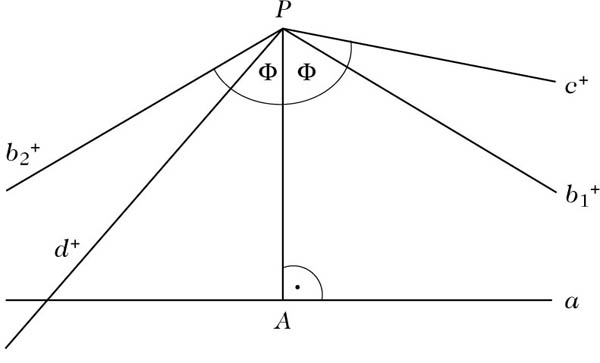
Um in der hyperbolischen Geometrie die Parallelität von Geraden zu definieren, wird der Parallelwinkel φ betrachtet. Es handelt sich dabei für eine gegebene Gerade a und einen nicht auf a liegenden Punkt P um den kleinsten Winkel zwischen einer Geraden b durch P, die mit a in einer Ebene liegt und a nicht schneidet, und dem Lot von P auf a. Dieser Parallelwinkel (oder Grenzwinkel) ist auf beiden Seiten des Lotes gleich groß.

Die Halbgeraden \begin{eqnarray}{b}_{1}^{+}\end{eqnarray} und \begin{eqnarray}{b}_{2}^{+}\end{eqnarray} mit dem Anfangspunkt P, für die \begin{eqnarray}\angle (P{A}^{+},{b}_{1}^{+})=\angle (P{A}^{+},{b}_{2}^{+})=\phi \end{eqnarray} gilt (wobei φ Parallelwinkel in P in Bezug auf a und A Fußpunkt des Lotes von P auf a ist), haben mit der Geraden a keinen Punkt gemeinsam.

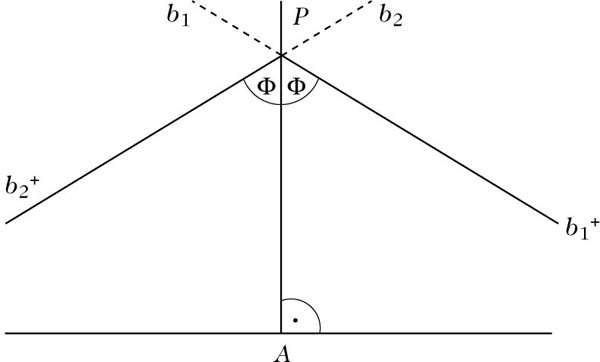
Gleiches gilt für jede Halbgerade c⁺ mit dem Anfangspunkt P und ∠(PA⁺, c⁺) > φ. Ist dagegen d⁺ eine Halbgerade mit ∠(PA⁺, d⁺) < φ, so schneidet d⁺ die Gerade a. Die Geraden b₁ und b₂, denen die Halbgeraden \begin{eqnarray}{b}_{1}^{+}\end{eqnarray} und \begin{eqnarray}{b}_{2}^{+}\end{eqnarray} angehören. sind Grenzgeraden in der Gesamtheit aller Geraden, die durch P verlaufen und a nicht schneiden und werden als zu a parallele Geraden bezeichnet. Die so definierte Parallelität ist symmetrisch und transitiv.

Zwei Geraden einer Ebene, die keinen gemeinsamen Punkt besitzen und nicht parallel sind, heißen divergierend. Zwei divergierende Geraden besitzen stets eine gemeinsame Senkrechte, dagegen gibt es zu zwei parallelen Geraden in keinem Falle eine Gerade, die auf den beiden Parallelen senkrecht steht. Es gilt sogar, daß es keine Gerade gibt, die mit zwei parallelen Geraden gleiche Stufen- oder Wechselwinkel bildet.

IV. Die Lobatschewskische Funktion Π

Eine fundamentale Eigenschaft der hyperbolischen Geometrie besteht darin, daß der Parallelwinkel in einem Punkt P in Bezug auf eine Gerade g nur vom Abstand x des Punktes P von der Geraden g abhängt. Der Parallelwinkel läßt sich somit als Funktion des Abstandes x auffassen: \begin{eqnarray}\phi ={\rm{\Pi }}(x),\end{eqnarray} wobei Π als Lobatschewskische Funktion bezeichnet wird.

Der Definitionsbereich dieser Funktion ist (0, ∞). ihr Wertebereich \begin{eqnarray}(0,\frac{\pi }{2})\end{eqnarray}. Π ist auf ihrem gesamten Definitionsbereich stetig sowie streng monoton fallend und besitzt folgende uneigentliche Grenzwerte: \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to \infty }{\rm{\Pi }}(x)=0,\quad \mathop{\mathrm{lim}}\limits_{x\to {0}^{+}}{\rm{\Pi }}(x)=\frac{\pi }{2}.\end{eqnarray}

Aus dem zweiten dieser Grenzwerte ergibt sich, daß für sehr gering ausgedehnte Bereiche der Parallelwinkel nahezu gleich \begin{eqnarray}\frac{\pi }{2}\end{eqnarray} ist, damit sind die beiden Parallelen zu einer Geraden durch einen Punkt kaum voneinander zu unterscheiden. Alle Eigenschaften der hyperbolischen Geometrie nähern sich deshalb in sehr kleinen Bereichen denen der euklidischen Geometrie an, da die Unterschiede beider Geometrien nur auf den verschiedenen Parallelenaxiomen beruhen. Das bedeutet, daß sich aus der Kenntnis „sehr kleiner Teile“ eines Raumes nicht genau bestimmen läßt, ob es sich um einen euklidischen oder einen nichteuklidischen Raum handelt.

Analytisch läßt sich die Lobatschewskische Funktion durch die Gleichung \begin{eqnarray}{\rm{\Pi }}(x)=2\cdot \arctan \exp \left(-\frac{x}{R}\right)\end{eqnarray} darstellen, die u. a. benötigt wird, um die Formeln der hyperbolischen Trigonometrie herzuleiten.

Eine sehr wichtige Schlußfolgerung aus der Existenz der Lobatschewskischen Funktion Π besteht darin, daß es in der hyperbolischen Geometrie eine absolute Länge gibt. Durch einen gestreckten Winkel (bzw. Teile eines solchen, die beispielsweise durch Halbierung gewonnen werden können) sind in der euklidischen Geometrie absolute Winkelgrößen gegeben, die sich durch eine abstrakte Vorschrift beschreiben lassen. So ist die Größe eines rechten Winkels durch die Konstruktionsbeschreibung „Errichtung der Senkrechten“ gegeben und bedarf keiner willkürlich festgelegten Eichhilfen, wie des Einheitsmeters. Im Gegensatz dazu gibt es in der euklidischen Geometrie keine absoluten Streckengrößen. In der hyperbolischen Geometrie existieren derartige absolute Längen. Sie lassen sich aus absoluten Winkeln mittels der Umkehrfunktion der Funktion Π ermitteln. Beispielsweise wird durch \begin{eqnarray}l:={{\rm{\Pi }}}^{-1}\left(\frac{\pi }{4}\right)\end{eqnarray} eine Länge l ausgezeichnet, die keinerlei Willkür unterliegt.

Die Existenz einer absoluten Länge ist mit der Nichtexistenz ähnlicher Figuren verbunden. Das<?PageNum _460 Vorhandensein ähnlicher Figuren (die nur in der euklidischen Geometrie existieren) schließt die Möglichkeit der Bestimmung absoluter Längen aus.

V. Modelle der hyperbolischen Geometrie

Um die Widerspruchsfreiheit der hyperbolischen Geometrie (und gleichbedeutend damit die Unabhängigkeit des Parallelenaxioms des Euklid von den Axiomen der absoluten Geometrie) nachzuweisen sowie eine anschauliche Interpretation der hyperbolischen Geometrie zu geben, werden die Grundbegriffe der hyperbolischen Geometrie durch bekannte Objekte der euklidischen (oder projektiven) Geometrie interpretiert. Dabei sind sehr unterschiedliche Interpretationen (Modelle) möglich. Zu den bekanntesten zählen die Poincaré-Halbebene, die Poincaré-Kreisscheibe sowie das Kleinsche Modell, bei denen die zweidimensionale hyperbolische Geometrie innerhalb einer offenen Halbebene bzw. einer offenen Kreisscheibe der euklidischen Ebene aufgebaut wird.

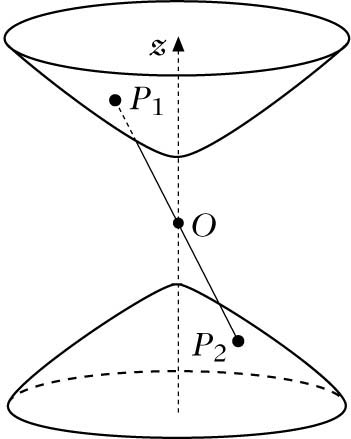
Eines der interessantesten Modelle der hyperbolischen Geometrie ist das pseudoeuklidische Modell, bei dem die Analogie zur sphärischen Geometrie (die ihrerseits ein Modell der elliptischen Geometrie ist) gut sichtbar wird. Die hyperbolische Ebene wird hierbei als Sphäre H mit imaginärem Radius innerhalb eines dreidimensionalen pseudoeuklidischen Raumes modelliert. (Aus euklidischer Sicht ist diese Sphäre ein zweischaliges Rotationshyperboloid, aus der Sicht der hyperbolischen Geometrie eine Ebene.) Hyperbolische Punkte sind bei diesem Modell alle diametralen Punktepaare auf H, also Paare von Punkten, die auf einer Geraden durch den Koordinatenursprung liegen (siehe Abbildung – die euklidischen Punkte P₁ und P₂ werden als ein H-Punkt identifiziert).

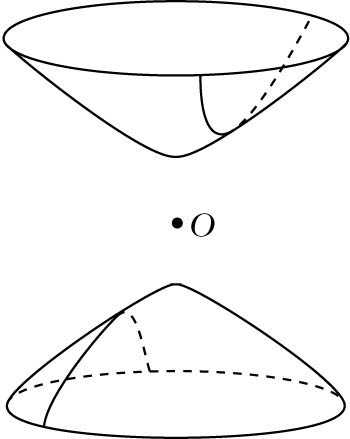
Hyperbolische Geraden sind alle Schnittkurven der hyperbolischen Ebene H mit (euklidischen) Ebenen, die durch den Mittelpunkt bzw. Koordinatenursprung verlaufen. Pseudoeuklidisch gesehen handelt es sich bei diesen Geraden also um Großkreise und euklidisch um Hyperbeln.

Hyperbolische Abstände von Punkten werden im pseudoeuklidischen Modell als Längen von Großkreisbögen, welche die entsprechenden Punkte miteinander verbinden, definiert (wobei es sich bei diesen Großkreisbögen euklidisch gesehen um Hyperbelbögen handelt). Wie in der sphärischen Geometrie besteht ein Zusammenhang zwischen der Länge des Großkreisbogens zwischen zwei Punkten und dem Winkel ihrer Radiusvektoren, wobei hier die Winkel pseudoeuklidisch zu messen sind (pseudoeuklidischer Raum).

Durch Projektion der oberen Schale des Hyperboloids (mit dem Radius i) vom Koordinatenursprung aus auf die Ebene z = 1 entsteht aus dem pseudoeuklidischen Modell der hyperbolischen Geometrie das Kleinsche Modell.

VI. Hyperbolische Geometrie als Geometrie auf einer Fläche konstanter negativer Krümmung

So wie die Elliptische Geometrie als Geometrie auf einer (Hyper-)Fläche konstanter positiver Krümmung und die euklidische Geometrie als Geometrie auf einer Fläche der Krümmung Null aufgefaßt werden können, läßt sich die hyperbolische Geometrie als Geometrie auf einer Fläche konstanter negativer Krümmung interpretieren. Innerhalb des pseudoeuklidischen Raumes besitzt eine Sphäre mit imaginärem Radius (siehe V.) eine konstante negative Krümmung, für r = i ist z. B. \begin{eqnarray}k=\frac{1}{{r}^{2}}=-1.\end{eqnarray}

Innerhalb des euklidischen Raumes ist die Pseudosphäre eine Fläche konstanter negativer Krümmung (der Name weist auf die Verwandtschaft mit der Sphäre als Fläche konstanter positiver Krümmung hin). Es handelt sich dabei um die Rotationsfläche der Traktrix (auch als Schleppkurve bekannt). Diese Pseudosphäre wird durch folgende Parameterdarstellung (mit den Parametern ϱ und λ sowie<?PageNum _461 einer Konstante R) beschrieben: \begin{eqnarray}\begin{array}{lll}x & = & \varrho \cdot \cos \lambda, \\ y & = & \varrho \cdot \sin \lambda, \\ z & = & R\cdot \mathrm{ln}\frac{R+\sqrt{{R}^{2}-{\varrho }^{2}}}{\varrho }-\sqrt{{R}^{2}-{\varrho }^{2}}.\end{array}\end{eqnarray}

Die Krümmung der Pseudosphäre ist in jedem ihrer Punkte \begin{eqnarray}k=-\frac{1}{{R}^{2}}\end{eqnarray}.

Die Geometrie auf der Pseudosphäre wurde um 1840 durch Minding eingehend untersucht. ohne daß dieser jedoch einen Bezug zu den Erkenntnissen von Bolyai. Gauss und Lobatschewski hergestellte.

Beltrami schuf 1868 auf Grundlage der Untersuchungen Mindings das erste Modell der hyperbolischen Geometrie und trug damit maßgeblich zu deren Akzeptanz bei.

Literatur

[1] Efimov N. W.: Höhere Geometrie. Deutscher Verlag der Wissenschaften Berlin 1960.

[2] Filler A.: Euklidische und nichteuklidische Geometrie. B.I. Wissenschaftsverlag Mannheim. 1993.

[3] Gans D.: An Introduction to Non-Euclidean Geometry. Academic Press Inc. San Diego_t 1973.

[4] Reichardt H.: Gauß und die Anfänge der nicht euklidischen Geometrie. mit Originalarbeiten von J. Bolyai, N. I. Lobatschewski und Felix Klein. Teubner Leipzig, 1985.

[5] Riemann B.: „Über die Hypothesen welche der Geometrie zugrunde liegen“ in: Das Kontinuum und andere Monographien (Reprint). Chelsea. 1973.