Lexikon der Mathematik: μ-Integral
Verallgemeinerung des Lebesgue-Integrals bzgl. des Maßraumes durch Young und Frechet.
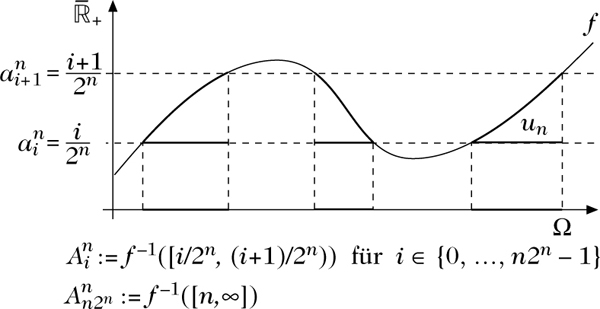
Es sei \(({\rm{\Omega }},{\mathcal{A}},\mu )\) ein Maßraum und \(f:{\rm{\Omega }}\to \bar{{\mathbb{R}}}\) eine meßbare Funktion. Unter der Annahme, daß f nicht-negativ ist, existiert eine isotone Folge (un|n ∈ ℕ) von Elementarfunktionen
\begin{eqnarray}{u}_{n}:=\displaystyle \sum _{i=1}^{n{2}^{n}}{a}_{i}^{n}{1}_{{A}_{i}^{n}}\end{eqnarray}
\begin{eqnarray}\displaystyle \int fd\mu :=\mathop{\sup }\limits_{n\in {\mathbb{N}}}\displaystyle \int {u}_{n}d\mu :=\mathop{\sup }\limits_{n\in {\mathbb{N}}}\displaystyle \sum _{i=1}^{n}{a}_{i}^{n}\mu ({A}_{i}^{n}),\end{eqnarray}
und zeigt, daß ∫fdμ von der speziellen Wahl der Folge (un|n ∈ ℕ) unabhängig ist.Ist f allgemein meßbar, so existiert eine Zerlegung f = f+ − f− von f in die Differenz zweier nicht-negativer meßbarer Funktionen f+ und f−, und man definiert das μ-Integral von f durch
\begin{eqnarray}\displaystyle \int fd\mu =\displaystyle \int {f}^{+}d\mu -\displaystyle \int {f}^{-}d\mu ,\end{eqnarray}
Beispiel für die Wahl von (un|n ∈ ℕ)
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.